【NOI2013】树的计数

#122. 【NOI2013】树的计数

 统计

•  描述
•  提交
•  自定义测试

我们知道一棵有根树可以进行深度优先遍历（DFS）以及广度优先遍历（BFS）来生成这棵树的 DFS 序以及 BFS 序。两棵不同的树的 DFS 序有可能相同，并且它们的 BFS 序也有可能相同，例如下面两棵树的 DFS 序都是 1 2 4 5 3，BFS 序都是 1 2 3 4 5。

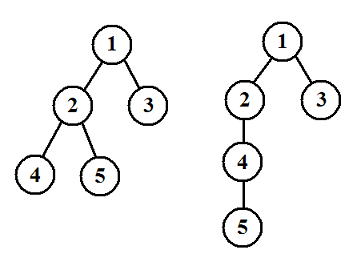
现给定一个 DFS 序和 BFS 序，我们想要知道，符合条件的有根树中，树的高度的平均值。即，假如共有 KK 棵不同的有根树具有这组 DFS 序和 BFS 序，且他们的高度分别是 h1,h2,…,hKh1,h2,…,hK，那么请你输出：

h1+h2+⋯+hKKh1+h2+⋯+hKK

输入格式

第一行包含 11 个正整数 nn，表示树的节点个数。

第二行包含 nn 个正整数，是一个 1∼n1∼n 的排列，表示树的 DFS 序。

第三行包含 nn 个正整数，是一个 1∼n1∼n 的排列，表示树的 BFS 序。

输入保证至少存在一棵树符合给定的两个序列。

输出格式

仅包含 11 个实数，四舍五入保留恰好三位小数，表示树高的平均值。

样例一

input

5 
1 2 4 5 3 
1 2 3 4 5

output

3.500

限制与约定

如果输出文件的答案与标准输出的差不超过 10−310−3，则将获得该测试点上的分数，否则不得分。

20% 的测试数据，满足：n≤10n≤10；

40% 的测试数据，满足：n≤100n≤100；

85% 的测试数据，满足：n≤2000n≤2000；

100% 的测试数据，满足：2≤n≤2000002≤n≤200000。

时间限制：1s1s

空间限制：256MB256MB

说明

树的高度：一棵有根树如果只包含一个根节点，那么它的高度为 11。否则，它的高度为根节点的所有子树的高度的最大值加 11。

对于树中任意的三个节点 a,b,ca,b,c，如果 a,ba,b 都是 cc 的儿子，则 a,ba,b 在 BFS 序中和 DFS 序中的相对前后位置是一致的，即要么 aa 都在 bb 的前方，要么 aa 都在 bb 的后方。

下载

样例数据下载

　　

#include<cstdio>
#include<cstring>
#include<vector>
#define set(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
#define EF if(ch==EOF) return x;
using namespace std;
typedef long long ll;
const int N=2005;
int n,xb[N],cb[N],q[N],dep[N],fa[N],ans[N];bool vis[N];
vector<int>e[N];double res;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;EF;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline bool bfs(){
    memset(vis,0,n+2);
    int h=0,t=1;q[t]=xb[1];vis[xb[1]]=1;
    while(h!=t){
        int x=q[++h];
        for(int i=0;i<e[x].size();i++){
            if(!vis[e[x][i]]){
                vis[e[x][i]]=1;
                q[++t]=e[x][i];
            }
        }
    }
    for(int i=1;i<=n;i++) if(q[i]!=cb[i]) return 0;
    return 1;
}
void dfs(int cur,int de,int h){
    if(cur>=n){
        if(bfs()) ans[++ans[0]]=h;
        return ;
    }
    int x=xb[cur],y=xb[cur+1],z=fa[x];
    dep[x]=de;
    fa[y]=x;
    e[x].push_back(y);
    dfs(cur+1,dep[x]+1,max(h,dep[x]+1));
    e[x].pop_back();
    for(;z;z=fa[z]){
        fa[y]=z;
        e[z].push_back(y);
        dfs(cur+1,dep[z]+1,max(h,dep[z]+1));
        e[z].pop_back();
    }
}
int main(){
    set(count);
    n=read();
    for(int i=1;i<=n;i++) xb[i]=read();
    for(int i=1;i<=n;i++) cb[i]=read();
    dfs(1,1,1);
    for(int i=1;i<=ans[0];i++) res+=ans[i];
    res/=1.0*ans[0];
    ll ANS=res*10000;
    ll ANS1=ANS/10000;
    ll ANS2=ANS%10000/10;
    printf("%lld.%lld
",ANS1,ANS2);
    return 0;
}

——转自网络：

考虑到 BFS 序的性质，BFS 在前的点的深度一定小于等于后面的点。所以我们考虑根据 BFS 序计算答案。

首先根据 BFS 序给树上的点重编号，按 BFS 序的先后编成 1,2,...,N，考虑相邻的点 i 对答案的贡献，如果它和 i−1必须在不同的层，那么对答案的贡献为 1，如果它和 i−1必须在同一层，那么对答案的贡献为 0 ，否则为 0.5 ，最后只需要把所有的贡献加起来就行了 (1,2号点的贡献应该强制为1)。

必须不在同一层很好判断，考虑一下必须在同一层的情况，如果点i在 DFS 序中的位置在点 i−1 前面的话，那么就一定在不同层。

否则只剩下在必须在同一层或者都可以。

在同一层和不同层都可以的情况，显然需要满足 DFS 序中 i−1,i 两个点必须是连续的。我们画图发现，如果在一棵按 BFS 序编号的树中，点 i 可以变作 i−1 的儿子的并且不改变 DFS,BFS 序的话，只能是 i 变换后， i 所在的那一层只有 i 一个点并且 i,i−1 应该有共同的父亲，那么这个条件等价于 1~~i−1 号点在 DFS 序中 1~~l 的一段和 r~~N 的一段，也就是说在 DFS 序中必须是前面一段最后一段。然后其他情况就是必须在同一层了。

#include<ctime>
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int n,dfn[N],bfn[N],l[N],r[N];
struct buf{
    char z[1<<25],*s;
    buf():s(z){
        fread(z,1,1<<25,stdin);
    }
    operator int(){
        int x=0,f=1;
        for(;*s<'0'||*s>'9';s++)if(*s=='-')f=-1;
        for(;*s>='0'&&*s<='9';s++)x=x*10+*s-'0';
        return x*f;
    }
}R;
int main(){
    n=R;
    for(int i=1;i<=n;i++) dfn[R]=i;
    for(int i=1;i<=n;i++) bfn[i]=dfn[R];
    l[n+1]=n+1;
    for(int i=n;i;i--){
        l[i]=min(l[i+1],bfn[i]);
        r[i]=max(r[i+1],bfn[i]);
    }
    int ans(4);
    for(int i=2;i<n;i++){
        if(bfn[i]>bfn[i+1]) ans+=2;
        else if(bfn[i]+1==bfn[i+1]&&r[i+1]-l[i+1]+1==n-i) ans++;
    }
    printf("%d.%d00",ans>>1,(ans&1)*5);
    return 0;
}