开始进入树的学习,原题目链接:重建二叉树。
题目描述:
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
题目分析:
首先题目给出的数据是二叉树的遍历结果,分别为前序遍历和中序遍历。那么首先需要知道二叉树的遍历过程。可以参考博文:二叉树的四种遍历方式。
题中提到了前序遍历和中序遍历;就先说一下两种遍历的步骤。
1.前序遍历:
先访问根节点,然后再前序遍历左子树;最后再前序遍历右子树。
很明显可以发现使用递归实现的。其具体效果看下图所示:

前向遍历的结果:ABDFECGHI。
2.中序遍历:先中序遍历根节点的左子树,然后遍历根节点,最后遍历根节点的右子树。
也可以很明显的发现使用递归来实现的,具体效果如下图所示:
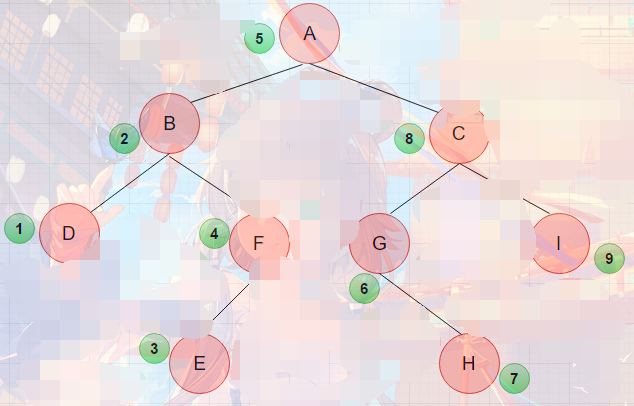
中序遍历的结果:DBEFAGHCI
其余的遍历就不在这里说了,请参看上面的博文。
知道了遍历的情况;根据这两个遍历结果可以发现,前序遍历的第一个就是根节点,然后中序遍历的该节点的前面就是左子树的结点;后年就是右子树的节点。
例如:
前序遍历序列{1,2,4,7,3,5,6,8}中根节点是1;{2,4,7}是左子树,
中序遍历序列{4,7,2,1,5,3,8,6}中根节点1的前面{4,7,2}是左子树,
再针对两种遍历的左子树继续进行如上操作,便可以得到根节点的左子树;同理也能如此得到右子树。
根据递归实现的代码如下:
1 public TreeNode reConstructBinaryTree(int [] pre,int [] in) { 2 if(pre == null || in == null || pre.length != in.length){ 3 return null; 4 } 5 6 return createBinaryTree(pre,0,pre.length-1, in, 0, in.length-1); 7 } 8 9 /** 10 * 创建二叉树 11 * @param pre 前序遍历序列 12 * @param preStart 前序遍历序列起始位 13 * @param preEnd 前序遍历序列结束位 14 * @param in 中序遍历序列 15 * @param inStart 中序遍历序列起始位 16 * @param inEnd 中序遍历序列结束位 17 * @return 二叉树的根节点 18 */ 19 public TreeNode createBinaryTree(int[] pre, int preStart, int preEnd, int[] in, int inStart, int inEnd){ 20 if(preStart > preEnd || inStart > inEnd){ 21 return null; 22 } 23 //取出前序遍历的首个元素,就是根节点 24 int root = pre[preStart]; 25 //寻找中序遍历中的根节点位置 26 int index = inStart; 27 for(;index <= inEnd; index++){ 28 if(in[index] == root){ 29 break; 30 } 31 } 32 //将当前节点加入树中 33 TreeNode tree = new TreeNode(root); 34 tree.left = createBinaryTree(pre,preStart+1, preStart+index-inStart, in, inStart, index-1); 35 tree.right = createBinaryTree(pre,preStart+index-inStart+1, preEnd, in, index+1, inEnd); 36 37 return tree; 38 }
代码已通过,参考了此博主的代码:https://www.cnblogs.com/zywu/p/5758917.html