数据结构-01| 数组

 

1. 数据结构概述

数据结构的介绍

　　1)  数据结构是一门研究算法的学科，只从有了编程语言也就有了数据结构.学好数据结构可以编写出更加漂亮,更加有效率的代码。

　　2)  要学习好数据结构就要多多考虑如何将生活中遇到的问题,用程序去实现解决.

　　3)  程序 = 数据结构 + 算法

2. 数组

在大部分编程语言中，数组都是从 0 开始编号的，但你是否下意识地想过，为什么数组要从 0 开始编号，而不是从 1 开始呢？

从数组存储的内存模型上来看，“下标”最确切的定义应该是“偏移（offset）”。如果用 a 来表示数组的首地址，a[0] 就是偏移为 0 的位置，也就是首地址，a[k] 就表示偏移 k 个 type_size 的位置，所以计算 a[k] 的内存地址只需要用这个公式：

a[k]_address = base_address + k * type_size
但是，如果数组从 1 开始计数，那我们计算数组元素 a[k] 的内存地址就会变为：a[k]_address = base_address + (k-1)*type_size
从 1 开始编号，每次随机访问数组元素都多了一次减法运算，对于 CPU 来说，就是多了一次减法指令。所以为了减少一次减法操作，数组选择了从 0 开始编号，而不是从 1 开始。
最主要的原因可能是历史原因。C 语言设计者用 0 开始计数数组下标，之后的 Java、JavaScript 等高级语言都效仿了 C 语言

2.1 概念

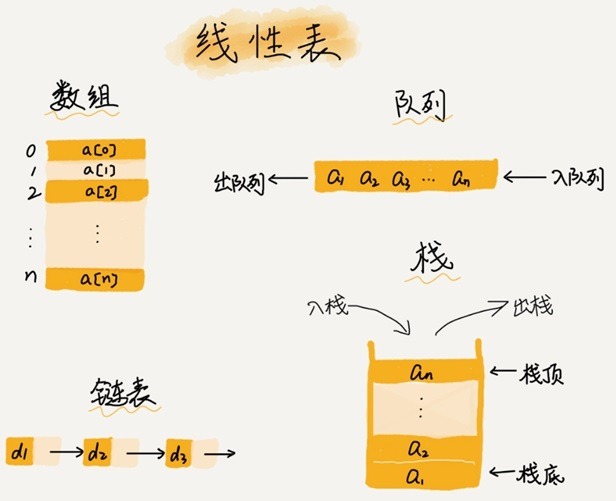
数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

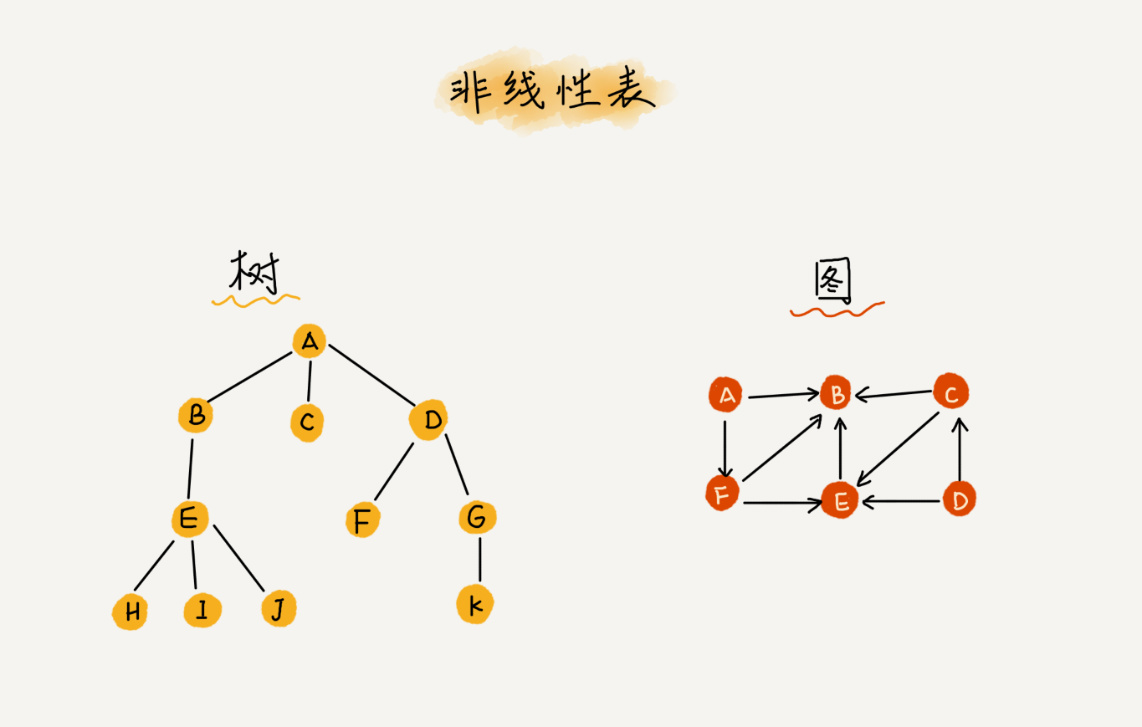
　　① 线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组，链表、队列、栈等也是线性表结构。与之对立的是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。

　　② 连续的内存空间和相同类型的数据。正是因为这两个限制，它才有了一个堪称“杀手锏”的特性：“随机访问”。但有利就有弊，这两个限制也让数组的很多操作变得非常低效，比如要想在数组中删除、插入一个数据，为了保证连续性，就需要做大量的数据搬移工作。

                    

 

2.2 数组是如何根据下标随机访问元素

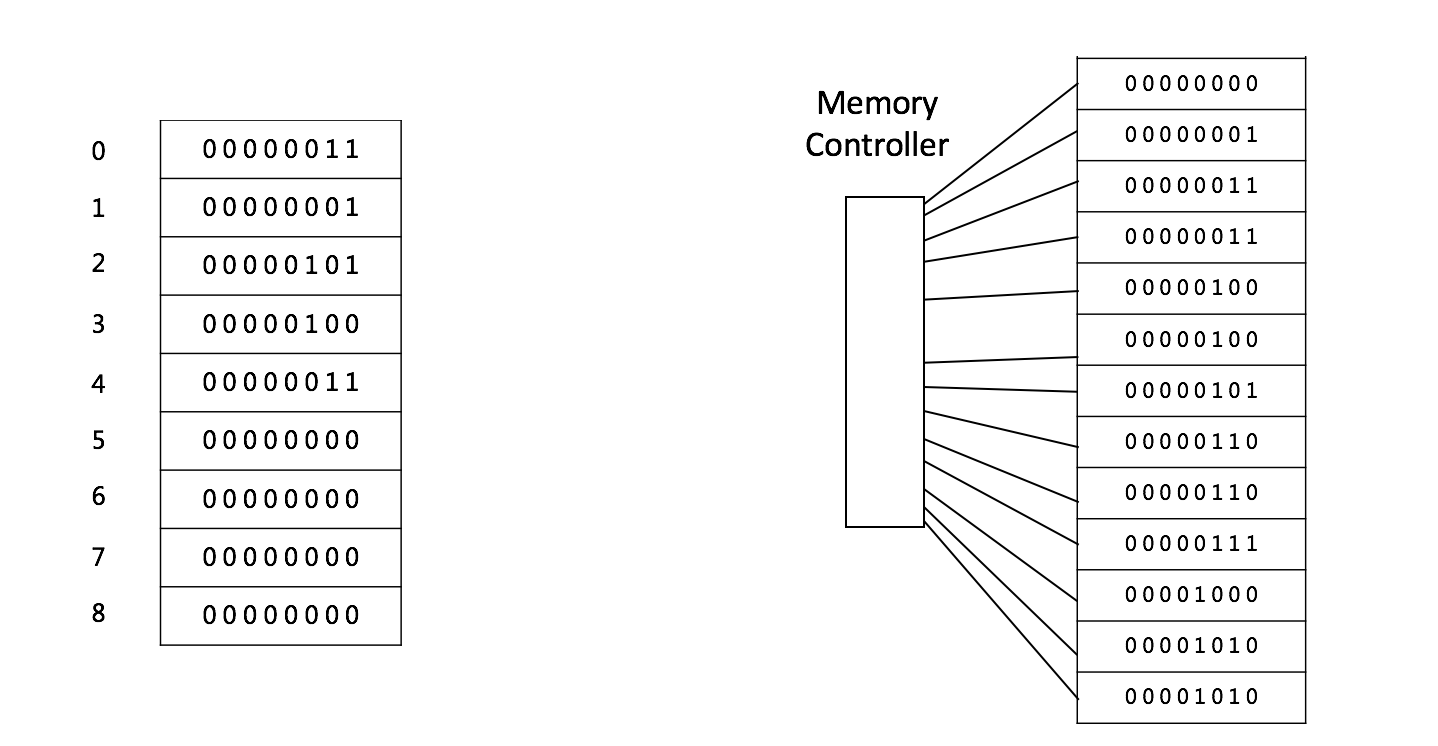
 数组-是内存中一段连续的存储空间，0--8是数组的下标；8位的数字是它的内存地址（简单示例），

 通过 Memory-Controller内存管理器可以实现随机访问任何一个下标里的内存元素，即数组元素； 访问查找数组它的时间复杂度是O(1)，因为它的硬件可以保证；

 计算机会给每个内存单元分配一个地址，计算机通过地址来访问内存中的数据。当计算机需要随机访问数组中的某个元素时，它会首先通过下面的寻址公式，计算出该元素存储的内存地址： a[i]_address = base_address + i * data_type_size（数组中每个元素的大小）

数组和链表的区别，

   很多人都回答说，“链表适合插入、删除，时间复杂度 O(1)； 数组适合查找，查找时间复杂度为 O(1)”。

   实际上，这种表述是不准确的。数组是适合查找操作，但是查找的时间复杂度并不为 O(1)。即便是排好序的数组，你用二分查找，时间复杂度也是 O(logn)。

   所以，正确的表述应该是，数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)。

 　　数组具有随机访问的特点，常用的二分查找算法需要用数组来存储数据。但如果我们选择链表这种数据结构，二分查找算法就无法工作了，因为链表并不支持随机访问。

2.3 低效的“插入”和“删除”

  对于插入和删除操作，为了保证数组元素是连续的，如D要插入下标3的位置，则要把EFG挪动到下标为4,5,6的位置，所以它的时间复杂度是O(n) -- 劣势所在；

　　如果插入到数组最后一个位置则它的时间复杂度是O(1)，如果是插入到第一个位置，则就是O(n)，平均时间复杂度就是O（2/n），就相当于是O(n)。  对于删除操作也是类似的；

　　插入操作：

　　假设数组的长度为 n，现在，如果我们需要将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾出来，给新来的数据，我们需要将第 k～n 这部分的元素都顺序地往后挪一位。那插入操作的时间复杂度是多少呢

如果在数组的末尾插入元素，那就不需要移动数据了，这时的时间复杂度为 O(1)。
但如果在数组的开头插入元素，那所有的数据都需要依次往后移动一位，所以最坏时间复杂度是 O(n)。 
因为我们在每个位置插入元素的概率是一样的，所以平均情况时间复杂度为 (1+2+…n)/n=O(n)。

如果数组中的数据是有序的，我们在某个位置插入一个新的元素时，就必须按照刚才的方法搬移 k 之后的数据。但是，如果数组中存储的数据并没有任何规律，数组只是被当作一个存储数据的集合。在这种情况下，如果要将某个数组插入到第 k 个位置，为了避免大规模的数据搬移，我们还有一个简单的办法就是：

• 直接将第 k 位的数据搬移到数组元素的最后，把新的元素直接放入第 k 个位置。

　　例子：假设数组 a[10] 中存储了如下 5 个元素：a，b，c，d，e。

我们现在需要将元素 x 插入到第 3 个位置。我们只需要将 c 放入到 a[5]，将 a[2] 赋值为 x 即可。最后，数组中的元素如下： a，b，x，d，e，c。

利用这种处理技巧，在特定场景下，在第 k 个位置插入一个元素的时间复杂度就会降为 O(1)。这个处理思想在快排中也会用到

　　删除：

　　要删除第 k 个位置的数据，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了。

和插入类似，如果删除数组末尾的数据，则最好情况时间复杂度为 O(1)；如果删除开头的数据，则最坏情况时间复杂度为 O(n)；平均情况时间复杂度也为 O(n)。

实际上，在某些特殊场景下，我们并不一定非得追求数组中数据的连续性。如果我们将多次删除操作集中在一起执行，删除的效率是不是会提高很多呢？

　　数组 a[10] 中存储了 8 个元素：a，b，c，d，e，f，g，h。现在，我们要依次删除 a，b，c 三个元素。

为了避免 d，e，f，g，h 这几个数据会被搬移三次，我们可以先记录下已经删除的数据。每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。
当数组没有更多空间存储数据时，我们再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。

如果你了解 JVM，你会发现，这不就是 JVM 标记清除垃圾回收算法的核心思想吗？

2.4 容器能否替代数组

如 Java 中的 ArrayList，在项目开发中，什么时候适合用数组，什么时候适合用容器呢？

　　ArrayList 最大的优势就是可以将很多数组操作的细节封装起来。比如前面提到的数组插入、删除数据时需要搬移其他数据等。另外，它还有一个优势，就是支持动态扩容。

数组本身在定义的时候需要预先指定大小，因为需要分配连续的内存空间。如果我们申请了大小为 10 的数组，当第 11 个数据需要存储到数组中时，我们就需要重新分配一块更大的空间，将原来的数据复制过去，然后再将新的数据插入。

　　如果使用 ArrayList，我们就完全不需要关心底层的扩容逻辑，ArrayList 已经帮我们实现好了。每次存储空间不够的时候，它都会将空间自动扩容为 1.5 倍大小。

不过，这里需要注意一点，因为扩容操作涉及内存申请和数据搬移，是比较耗时的。所以，如果事先能确定需要存储的数据大小，最好在创建 ArrayList 的时候事先指定数据大小。如：

ArrayList<User> users = new ArrayList(10000);
for (int i = 0; i < 10000; ++i) {
    users.add(xxx);
}

有些时候用数组会更合适些：
1.Java ArrayList 无法存储基本类型，比如 int、long，需要封装为 Integer、Long 类，而 Autoboxing、Unboxing 则有一定的性能消耗，所以如果特别关注性能，或者希望使用基本类型，就可以选用数组。
2. 如果数据大小事先已知，并且对数据的操作非常简单，用不到 ArrayList 提供的大部分方法，也可以直接使用数组。
3. 当要表示多维数组时，用数组往往会更加直观。比如 Object[][] array；而用容器的话则需要这样定义：ArrayList<ArrayList> array

　　对于业务开发，直接使用容器就足够了，省时省力。毕竟损耗一丢丢性能，完全不会影响到系统整体的性能。但如果是做一些非常底层的开发，比如开发网络框架，性能的优化需要做到极致，这个时候数组就会优于容器。

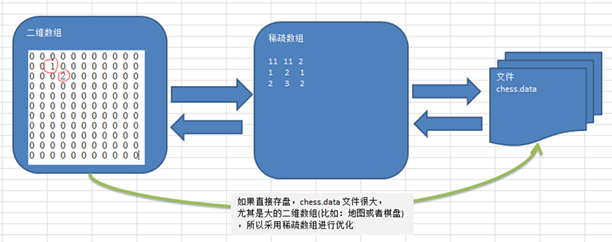
稀疏sparsearray数组

• 先看一个实际的需求

编写的五子棋程序中，有存盘退出和续上盘的功能。

当一个数组中大部分元素为０，或者为同一个值的数组时，可以使用稀疏数组来保存该数组。

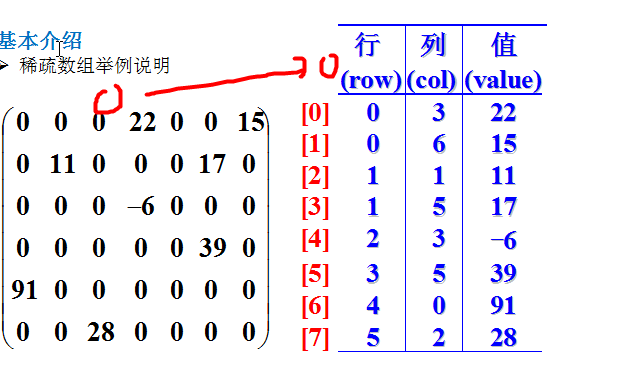
稀疏数组的处理方法是:

　　1)  记录数组一共有几行几列，有多少个不同的值(有效值的个数)

　　2)   把具有不同值的元素的行列及值记录在一个小规模的数组中，从而缩小程序的规模

      

 

  

代码实现：

object SparseArrayDemo {
  def main(args: Array[String]): Unit = {

    //1. 先把原始的地图创建(二维数组)
    val rows = 11
    val cols = 11
    val chessMap1 = Array.ofDim[Int](rows, cols)
    chessMap1(1)(2) = 1 //表示黑子
    chessMap1(2)(3) = 2 //表示蓝子
    chessMap1(4)(5) = 2
    chessMap1(5)(6) = 1

    //输出原始的地图
    println("原始的地图如下..")
    for (item1 <- chessMap1) {
      for (item2 <- item1) {
        printf("%d	", item2)
      }
      println()
    }

    //使用稀疏数组来对chessMap1进行压缩
    //思路
    //1. 使用ArrayBuffer 来保存有效数据
    //2. 每一个数据使用Node 对象来表示
    //3. Node 的结构 class Node(val row:Int, val col:Int,val value:Int)

    val sparseArray = ArrayBuffer[Node]()
    val node1 = new Node(rows, cols, 0)
    sparseArray.append(node1)

    //遍历chessMap1, 每发现一个非0的值，就创建给Node ,并加入到sparseArray
    for (i <- 0 until chessMap1.length) { //行
      for (j <- 0 until chessMap1(i).length) {
        //列
        if (chessMap1(i)(j) != 0) {
          //说明是一个需要保存的数据
          //Node 对象
          val node2 = new Node(i, j, chessMap1(i)(j))
          sparseArray.append(node2)
        }
      }
    }

    //输出稀疏数组
    println("稀疏数组的情况")
    for (node <- sparseArray) {
      printf("%d	%d	%d	
", node.row, node.col, node.value)
    }

    //将稀疏数组，恢复成原始的地图
    //1. 先从sparseArray 读取第一个node ,并创建新的地图
    val firstNode = sparseArray(0)
    val chessMap2 = Array.ofDim[Int](firstNode.row, firstNode.col)
    //2. 从sparseArray第二个数据开始遍历，并将数组恢复到chessMap2
    for (i <- 1 until sparseArray.length) {
      val node = sparseArray(i)
      chessMap2(node.row)(node.col) = node.value
    }

    //再次输出恢复后的原始地图
    println("恢复后原始的地图如下..")
    for (item1 <- chessMap2) {
      for (item2 <- item1) {
        printf("%d	", item2)
      }
      println()
    }


  }
}

//每一个数据使用Node 对象来表示
class Node(val row: Int, val col: Int, val value: Int)

 对于数组的插入和删除操作的改善  ===>> 链表

 3. 数组复杂度分析

Array的时间复杂度：

•  Access: O(1)
• prepend：O(1)
• append：O(1)
• lookup：O(1)
• Insert: 平均 O(n)
• Delete: 平均 O(n)

 Java中ArrayList ：

添加和删除操作如下：

/**
 330:    * Appends the supplied element to the end of this list.
 331:    * The element, e, can be an object of any type or null.
 332:    *
 333:    * @param e the element to be appended to this list
 334:    * @return true, the add will always succeed
 335:    */
 336:   public boolean add(E e)//加到数组最后
 337:   {
 338:     modCount++;
 339:     if (size == data.length)  //判断数组的size是否够，如果不够就增加；
 340:       ensureCapacity(size + 1);
 341:     data[size++] = e; //在末尾添加e元素, size++
 342:     return true;
 343:   }
 344: 
 345:   /**
 346:    * Adds the supplied element at the specified index, shifting all
 347:    * elements currently at that index or higher one to the right.
 348:    * The element, e, can be an object of any type or null.
 349:    *
 350:    * @param index the index at which the element is being added
 351:    * @param e the item being added
 352:    * @throws IndexOutOfBoundsException if index < 0 || index > size()
 353:    */
 354:   public void add(int index, E e)
 355:   {
 356:     checkBoundInclusive(index);
 357:     modCount++;
 358:     if (size == data.length)
 359:       ensureCapacity(size + 1);
 360:     if (index != size)
 361:       System.arraycopy(data, index, data, index + 1, size - index); //与上边不同的是会进行一轮拷贝的操作，参数data,index表示原位置;data,index+1表示它的目标位置;要做的就是把原位置的起点位置拷贝到目标地址的起点位置。 size-index表它的长度length，即数组后半部分要挪动的部分
 362:     data[index] = e;
 363:     size++;
 364:   }
160:   /**
 161:    * Guarantees that this list will have at least enough capacity to
 162:    * hold minCapacity elements. This implementation will grow the list to
 163:    * max(current * 2, minCapacity) if (minCapacity > current). The JCL says
 164:    * explictly that "this method increases its capacity to minCap", while
 165:    * the JDK 1.3 online docs specify that the list will grow to at least the
 166:    * size specified.
 167:    *
 168:    * @param minCapacity the minimum guaranteed capacity
 169:    */
 170:   public void ensureCapacity(int minCapacity) 
 171:   {
 172:     int current = data.length; //查询当前数组长度，
 173: 
 174:     if (minCapacity > current) //长度不够，就new一个当前长度 * 2
 175:       {
 176:         E[] newData = (E[]) new Object[Math.max(current * 2, minCapacity)];
 177:         System.arraycopy(data, 0, newData, 0, size); //然后把老数组的值拷贝到新数组中。 插入和删除操作大量的arraycopy，比较低效；
 178:         data = newData;
 179:       }
 180:   }