分类模型
- K近邻
- 逻辑斯谛回归
- 决策树
K近邻(KNN)
最简单最初级的分类器,就是将全部的训练数据所对应的类别都记录下来,当测试对象的属性和某个训练对象的属性完全匹配时,便可以对其进行分类
K近邻(k-nearest neighbour, KNN)是一种基本分类方法,通过测量不同特征值之间的距离进行分类。它的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别,其中K通常是不大于20的整数;
KNN算法中,所选择的邻居都是已经正确分类的对象
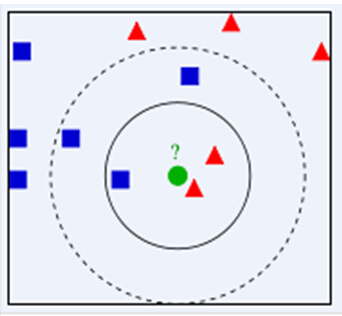
绿色圆(测试数据)要被决定赋予哪个类,是红色三角形还是蓝色四方形?
如果K=3(距离绿色圆最近的3个),由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,
如果K=5(距离绿色圆最近的5个),由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类;
KNN算法的结果很大程度取决于K的选择。
KNN距离计算
KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,避免了对象之间的匹配问题,在这里距离一般使用欧氏距离或曼哈顿距离:
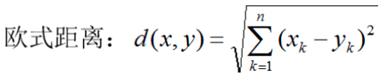
 (一般选择曼哈顿距离)
(一般选择曼哈顿距离)
KNN算法
在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类,其算法的描述为:
- 计算测试数据与各个训练数据之间的距离;
- 按照距离的递增关系进行排序;
- 选取距离最小的K个点;
- 确定前K个点所在类别的出现频率;
- 返回前K个点中出现频率最高的类别作为测试数据的预测分类。
代码的实现:
### 0.引入依赖 import numpy as np import pandas as pd # 这里直接引入sklearn里的数据集,iris鸢尾花 from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split # 切分数据集为训练集和测试集 from sklearn.metrics import accuracy_score # 计算分类预测的准确率
附:

print(iris.data.shape) #data对应了样本的4个特征,150行4列(150, 4) print(iris.data[:5]) # 显示样本特征的前5行 print(iris.target.shape) # target对应了样本的类别(目标属性),150行1列 print(iris.target) # 显示所有样本的目标属性; iris的每个样本都包含了品种信息,即目标属性(第5列,也叫target或label) ===> (150, 4) [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2]] (150,) [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
iris = load_iris() df = pd.DataFrame(data = iris.data, columns = iris.feature_names) df['class'] = iris.target df['class'] = df['class'].map({0: iris.target_names[0], 1: iris.target_names[1], 2: iris.target_names[2]}) df.head(10)
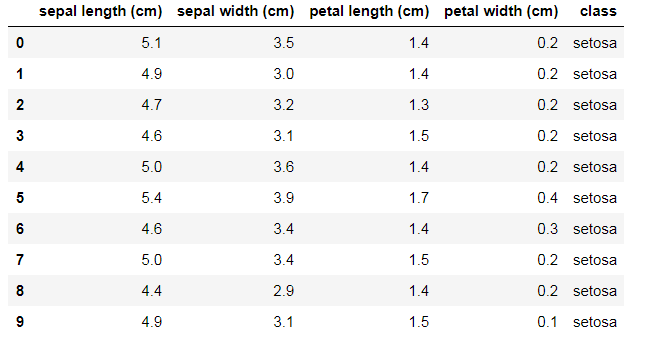
df.describe()

x = iris.data y = iris.target.reshape(-1,1) print(x.shape, y.shape) ===> (150, 4) (150, 1)
# 划分训练集和测试集 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=35, stratify=y) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) ==> (105, 4) (105, 1) (45, 4) (45, 1)
核心算法实现
# 距离函数定义 def l1_distance(a, b): return np.sum(np.abs(a-b), axis=1) #曼哈顿距离, 向量的绝对值,一阶距离 def l2_distance(a, b): return np.sqrt( np.sum((a-b) ** 2, axis=1) ) #二阶距离 # 分类器实现 class kNN(object): # 定义一个初始化方法,__init__ 是类的构造方法 def __init__(self, n_neighbors = 1, dist_func = l1_distance): self.n_neighbors = n_neighbors self.dist_func = dist_func # 训练模型方法 def fit(self, x, y): self.x_train = x self.y_train = y # 模型预测方法 def predict(self, x): # 初始化预测分类数组 y_pred = np.zeros( (x.shape[0], 1), dtype=self.y_train.dtype ) # 遍历输入的x数据点,取出每一个数据点的序号i和数据x_test for i, x_test in enumerate(x): # x_test跟所有训练数据计算距离 distances = self.dist_func(self.x_train, x_test) # 得到的距离按照由近到远排序,取出索引值 nn_index = np.argsort(distances) # 选取最近的k个点,保存它们对应的分类类别 nn_y = self.y_train[ nn_index[:self.n_neighbors] ].ravel() # 统计类别中出现频率最高的那个,赋给y_pred[i] y_pred[i] = np.argmax( np.bincount(nn_y) ) return y_pred
### 3. 测试
# 定义一个knn实例 knn = kNN(n_neighbors = 3) # 训练模型 knn.fit(x_train, y_train) # 传入测试数据,做预测 y_pred = knn.predict(x_test) print("分类准确率:{:.5f}%".format(accuracy_score(y_test,y_pred)*100)) ==> 分类准确率:93.33333%
测试L1和L2距离对准确率是否有比较大的影响?
# 定义一个knn实例 knn = kNN() # 训练模型 knn.fit(x_train, y_train) # 保存结果list result_list = [] # 针对不同的参数选取,做预测 for p in [1, 2]: knn.dist_func = l1_distance if p == 1 else l2_distance # 考虑不同的k取值,步长为2 for k in range(1, 10, 2): knn.n_neighbors = k # 传入测试数据,做预测 y_pred = knn.predict(x_test) # 求出预测准确率 accuracy = accuracy_score(y_test, y_pred) result_list.append([k, 'l1_distance' if p == 1 else 'l2_distance', accuracy]) df = pd.DataFrame(result_list, columns=['k', '距离函数', '预测准确率']) #选择 5 l2_distance的距离 df
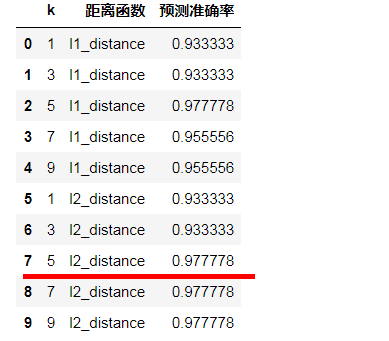
可得出 :
| 5 | l2_distance | 0.977778 |
KNN=5时,距离选取l2_distance,它的准确率是最高的。
决策树
决策树是一种简单高效并且具有强解释性的模型,广泛应用于数据分析领域。其本质是一颗自上而下的由多个判断节点组成的树;
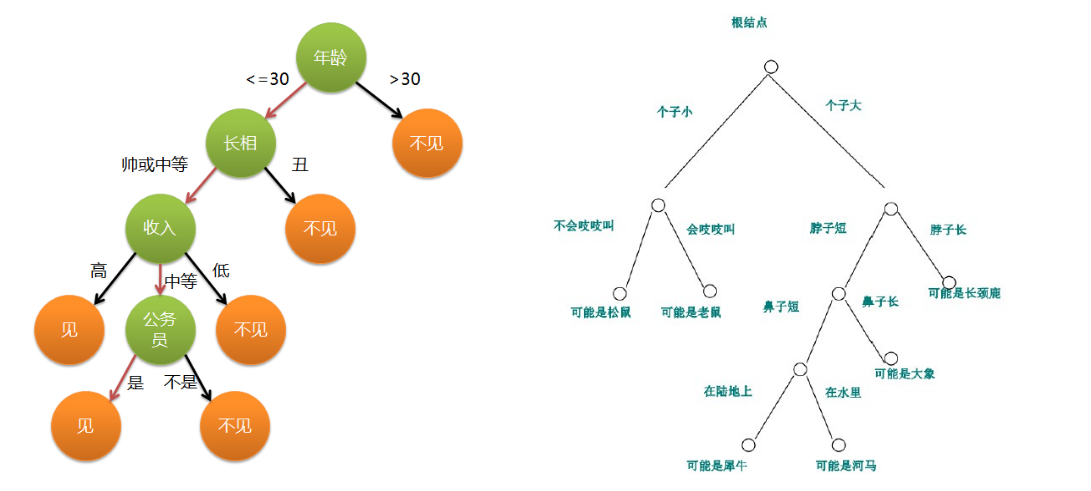
决策树示例:
预测小明今天是否会出门打球
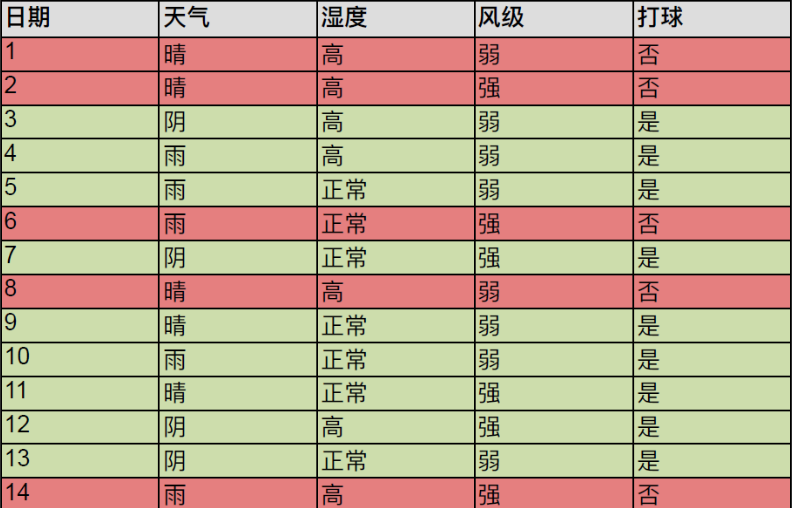

决策树与 if-then 规则
-
决策树可以看作一个 if-then 规则的集合
- 由决策树的根节点到叶节点的每一条路径,构建一条规则:路径上内部节点的特征对应着规则的条件(condition),叶节点对应规则的结论
- 决策树的 if-then 规则集合有一个重要性质:互斥并且完备。这就是说,每个实例都被一条规则(一条路径)所覆盖,并且只被这一条规则覆盖
决策树中的 Condition 是什么?
- Condition 的确定过程就是特征选择的过程;
决策树的目标:
- 决策树学习的本质,是从训练数据集中归纳出一组 if-then 分类规则
- 与训练集不相矛盾的决策树,可能有很多个,也可能一个也没有;所以我们需要选择一个与训练数据集矛盾较小的决策树
- 另一角度,我们可以把决策树看成一个条件概率模型,我们的目标是将实例分配到条件概率更大的那一类中去;
- 从所有可能的情况中选择最优决策树,是一个NP完全问题,所以我们通常采用启发式算法求解决策树,得到一个次最优解
- 采用的算法通常是递归地进行以下过程:选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集都有一个最好的分类
特征选择:
- 特征选择就是决定用哪个特征来划分特征空间

随机变量:
随机变量(random variable)的本质是一个函数,是从样本空间的子集到实数的映射,将事件转换成一个数值
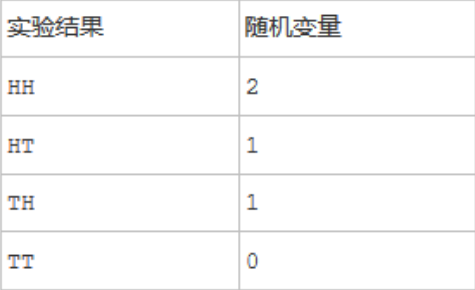
根据样本空间中的元素不同(即不同的实验结果),随机变量的值也将随机产生。可以说,随机变量是“数值化”的实验结果
在现实生活中,实验结果是描述性的词汇,比如 “硬币的正面”、“反面”。在数学家眼里,这些文字化的叙述太过繁琐,所以拿数字来代表它们
熵
熵(entropy)用来衡量随机变量的不确定性;变量的不确定性越大,熵也就越大
设X是一个取有限个值的离散随机变量,其概率分布为:
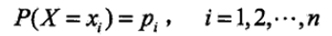
则随机变量X的熵定义为:
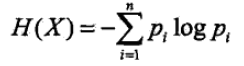
通常,上式中的对数以2为底或者以e为底(自然对数),这时熵的单位分别称为比特(bit)或纳特(nat)。
当随机变量只取两个值,例如 1,0 时,则 X 的分布为:

熵为: 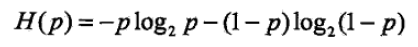
这时,熵H(p)随概率p变化的曲线如下图所示(单位为比特):
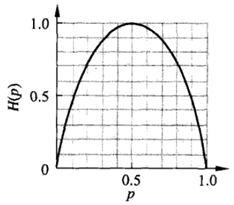
熵的示例
给三个球分类
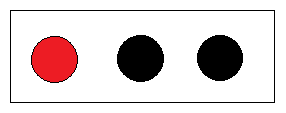
- 显然一眼就可以看出把红球独自一组,黑球一组;
- 那么从熵的观点来看,是什么情况呢?
初始状态的熵: E(三个球) = - 1/3 * log( 1/3 ) - 2/3 * log( 2/3 ) = 0.918
①第一种分类方法是一个红球、一个黑球一组,另一个黑球自己一组:
- 在红黑一组中有红球和黑球, 红黑球各自出现的概率是 1/2.
- 在另一组 100% 出现黑球, 红球的概率是 0
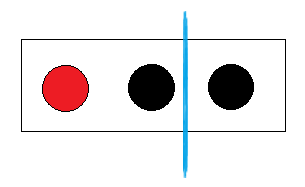
E(红黑|黑) = E(红黑) + E(黑) = - 1/2 * log( 1/2 ) - 1/2 * log ( 1/2 ) - 1 * log( 1 ) = 1; 可以看到,分类之后熵反而增大了
② 第二种分法就是红球自己一组,剩下两个黑球一组:
在红球组中出现黑球的概率是0, 在黑球组中出现红球的概率是0, 这样的分类已经“纯”了,也就是分类后子集中的随机变量已经变成确定性的了;
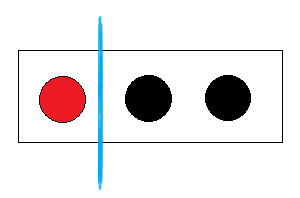
E(红|黑黑) = E(红) + E(黑黑) = - 1 * log( 1 ) - 1 * log( 1 ) = 0
决策树的目标
- 我们使用决策树模型的最终目的是利用决策树模型进行分类预测,预测我们给出的一组数据最终属于哪一种类别,这是一个由不确定到确定的过程;
- 最终理想的分类是,每一组数据,都能确定性地按照决策树分支找到对应的类别
- 所以我们就选择使数据信息熵下降最快的特征作为分类节点,使得决策树尽快地趋于确定
条件熵(conditional entropy)
条件熵 H( Y|X ) 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性:
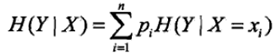 其中
其中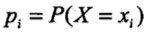
- 熵 H(D) 表示对数据集 D 进行分类的不确定性。
- 条件熵 H(D|A) 指在给定特征 A 的条件下数据集分类的不确定性
- 当熵和条件熵的概率由数据估计得到时,所对应的熵与条件熵分别称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy)
信息增益
特征A对训练数据集D的信息增益 g(D, A),定义为集合D的经验熵H(D)与特征A给定条件下D的条件熵 H(D|A)之差,即

- 决策树学习应用信息增益准则选择特征
- 经验熵H(D)表示对数据集D进行分类的不确定性。而经验条件熵H(D|A)表示在特征A给定的条件下对数据集D进行分类的不确定性。那么它们的差,即信息增益,就表示由于特征A而使得对数据集D的分类的不确定性减少的程度
- 对于数据集D而言,信息增益依赖于特征,不同的特征往往具有不同的信息增益
- 信息增益大的特征具有更强的分类能力
决策树的生成算法
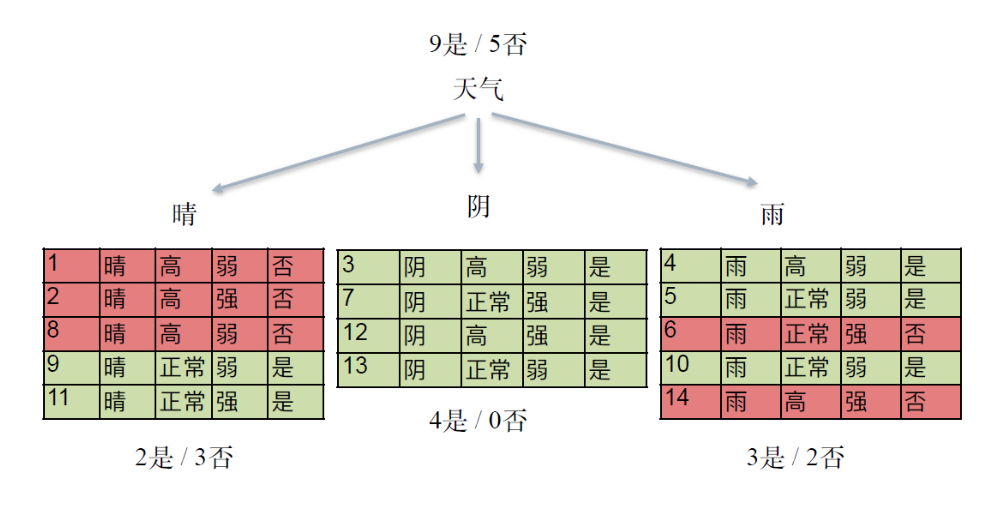
决策树(ID3)的训练过程就是找到信息增益最大的特征,然后按照此特征进行分类,然后再找到各类型子集中信息增益最大的特征,然后按照此特征进行分类,最终得到符合要求的模型;
C4.5算法在ID3基础上做了改进,用信息增益比来选择特征;
分类与回归树(CART): 由特征选择、树的生成和剪枝三部分组成,既可以用于分类也可以用于回归;
