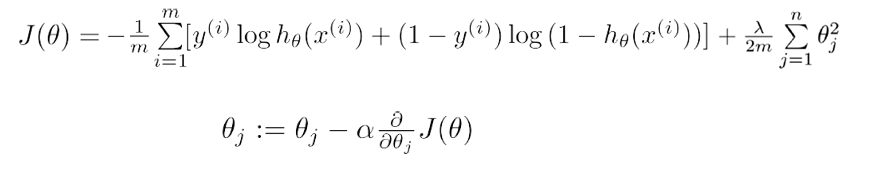逻辑斯蒂回归
线性回归的问题 —— 怎样判断肿瘤是否恶性?
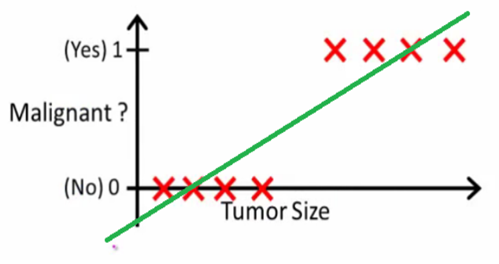
线性回归健壮性不够,一旦有噪声,立刻“投降”

逻辑斯蒂回归 —— 分类问题
Sigmoid函数(压缩函数) 0-1之间阶跃函数的平滑 -- 解决阶跃函数非线性度不够的问题
redu线性整流函数,比阶跃好点


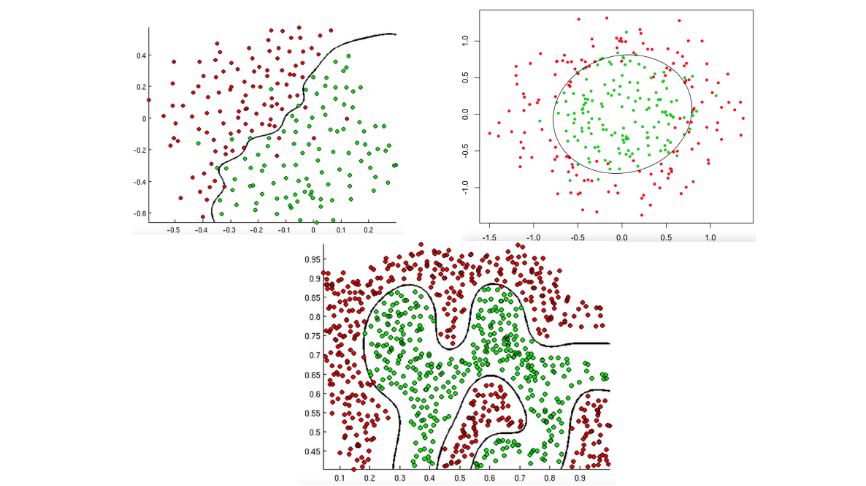
我们将线性回归拟合出来的值用压缩函数进行压缩,压缩完成后用 0.5 做一个概率的判定边界,就能把样本分成两类,即正样本和负样本;

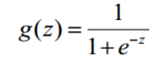
sigmoid函数中(神经网络中用的多),e-z 中 z 的正负决定了 g(z) 的值最后是大于 0.5 还是小于 0.5;即 z 大于 0 时,g(z) 大于 0.5,z 小于 0 时,g(z)小于 0.5
当 z 对应的表达式为分类边界时,恰好有分类边界两侧对应 z 正负不同,也就使得分类边界两边分别对应 g(z)>0.5 和 g(z)<0.5,因此根据 g(z) 与 0.5 的大小关系,就可以实现分类
逻辑斯谛回归损失函数
平方损失函数的问题

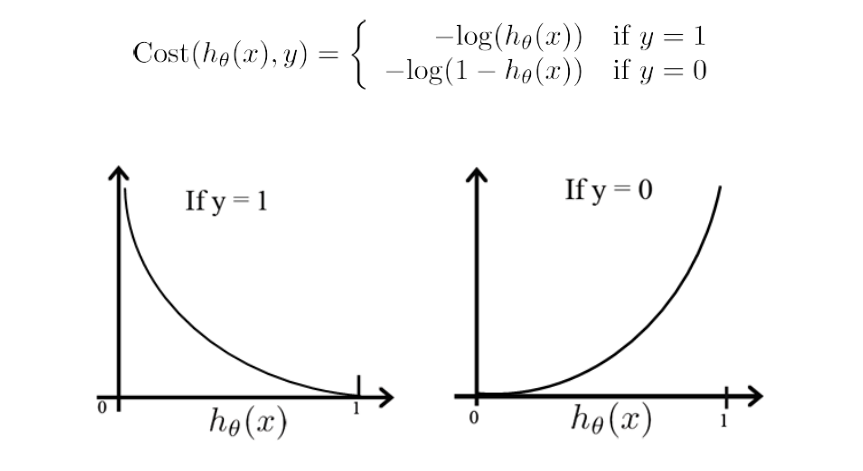
 h(oX)为预测值,y是真实值;
h(oX)为预测值,y是真实值;

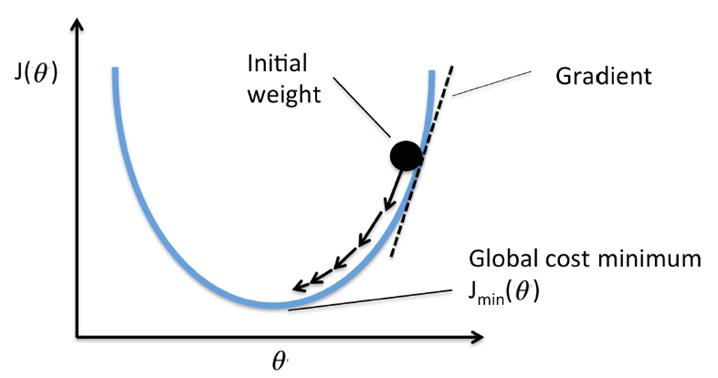
梯度下降法求解
机器学习or监督学习的目的就是这个梯度下降函数(损失函数 和正则画像)