首先观察到给定的(y)是没用的,激光最终会射到哪些接收器只会被(A)和(B)位置所影响。
(A)和(B)点的位置被(x_A)和(|x_A-x_B|)所决定。(L=|x_A-x_B|)。
现在假设我们已经确定了(x_A),还要选择一个(L)。假如说我们选择了一个(L),并且存在一个大于一个的奇数(k|L),那么我们可以选择一个新的(L'=frac LK),新的激光不仅会经过原来的关键点,还会多经过一些点。
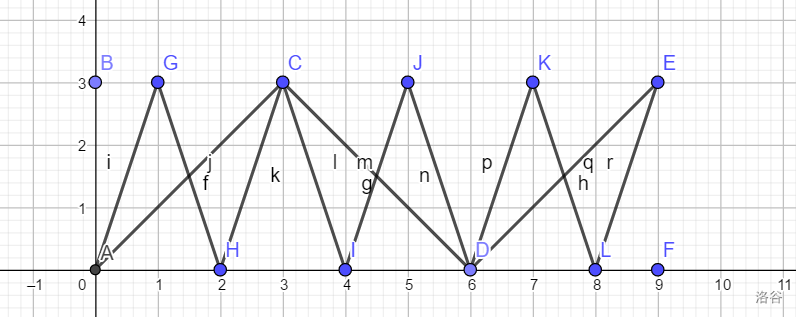
(vec{AC})就可以被(vec{AG}+vec{GH}+vec{HC})代替
所以我们选择的(L)不能被任意比一大的奇数整除,也就是说(L=2^n),这样的(L)最多有(log_210^9)个,枚举算即可
对于一个固定的(L),我们还需要算最优的(x_A),观察在下面的关键点(a_i)如果满足(|a_i-x_a|equiv0(mod~~2L))则会被射中,上面的关键点满足(b_i-x_aequiv L(mod~~2L)),则会被射中,所以开个(map),对于每个关键点让位置在(mod~~2L)意义下(x_a++)
注意特判(x_a=x_b),不然会反复纵跳
(O(nlognlog10^9))
#include<cstdio>
#include<map>
using namespace std;
const int N = 2e5 + 5;
int a[N],b[N],n,m,ans = 0,emp;
map<int,int>mp;
void check(int x){
mp.clear();
for(int i = 1;i <= n;++i)
++mp[a[i] % x];
for(int i = 1;i <= m;++i)
++mp[(b[i] + (x>>1)) % x];
for(auto v:mp)
ans = max(ans,v.second);
}
int main(){
scanf("%d%d",&n,&emp);
for(int i = 1;i <= n;++i)
scanf("%d",&a[i]);
scanf("%d%d",&m,&emp);
for(int i = 1;i <= m;++i)
scanf("%d",&b[i]);
for(int i = 1;i <= n;++i)
++mp[a[i]];
for(int i = 1;i <= m;++i)
++mp[b[i]];
for(auto v:mp)
ans = max(ans,v.second);
for(int i = 1;i <= 30;++i)
check(1<<i);
printf("%d",ans);
}