FFT实现(java)，验证(matlab)

 

 

java代码

compex类

public class Complex {
    private double a, b;
    public Complex(){
        this.a = 0.0;
        this.b = 0.0;
    }
    public Complex(double a, double b){
        this.a = a;
        this.b = b;
    }
    public Complex(Complex C){
        this.a = C.a;
        this.b = C.b;
    }
    public double getRealPart(){ //返回实部
        return a;
    } // 获取实部
    public double getImaginaryPart(){
        return b;
    } //获取虚部
    public String toString(){
        if(b != 0) {
            if (a == 0)
                return b + "i";
            else
                return a + "+" + b + "i";
        }
        else
            return a + "";

    }  //字符串表示复数
    public Complex plus(Complex C){
        if (C == null){
            System.out.println("对象为null");
            return new Complex();
        }
        return new Complex(this.a + C.a, this.b + C.b);
    } // 加法
    public Complex minus(Complex C){
        if (C == null){
            System.out.println("对象为null");
            return new Complex();
        }
        return new Complex(this.a - C.a, this.b - C.b);
    } // 减法
    public Complex multiply(Complex C){
        if (C == null){
            System.out.println("对象为null");
            return new Complex();
        }
        double newa = this.a * C.a - this.b * C.b;
        double newb = this.a * C.b + this.b * C.a;
        return new Complex(newa, newb);
    } // 乘法
    public Complex divide(Complex C){
        if (C == null){
            System.out.println("对象为null");
            return new Complex();
        }
        if(C.a == 0 && b == 0){
            System.out.println("除数不能为0！");
            return new Complex();
        }
        double newa = (this.a * C.a + this.b * C.b) / (C.a * C.a + C.b * C.b);
        double newb = (this.a * C.a - this.b * C.b) / (C.a * C.a + C.b * C.b);
        return new Complex(newa, newb);
    } // 除法

    public static void main(String[] args) {
        Complex x = new Complex(3,4);
        Complex y = new Complex(5,7);
        System.out.println("x:" + x.toString());
        System.out.println("y:" + y.toString());
        System.out.println("(x+y) = " + x.plus(y).toString());
        System.out.println("(x-y) = " + x.minus(y).toString());
        System.out.println("(x*y) = " + x.multiply(y).toString());
        System.out.println("(x/y) = " + x.divide(y).toString());
    }


}

FFT

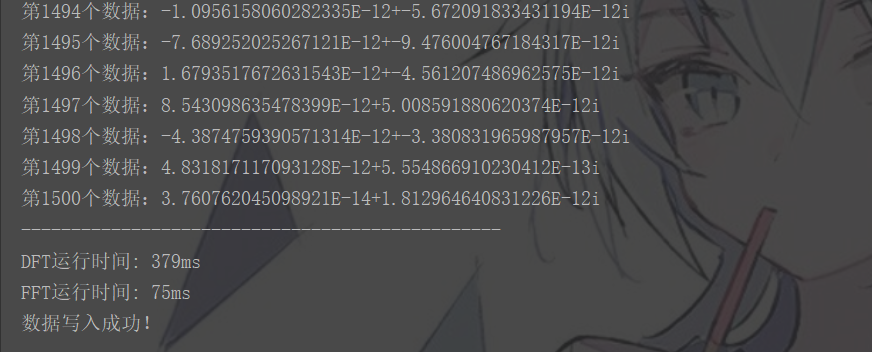
import java.io.*;

public class FFT {
    public static void CreateSignal(int length, Complex[] x){
        double Fs = 1000; // 采样频率
        double T = 1 / Fs; // 采样周期
        System.out.println("产生幅值为 0.7 的 50 Hz正弦量和幅值为 1 的 120 Hz正弦量(一共"+length+"个)");
        for (int i = 0; i < length; i++) {
            // 产生幅值为0.7的50Hz正弦量和幅值为1的120 Hz正弦量。
            double S = 0.7 * Math.sin(2 * Math.PI * 50 * i * T) + Math.sin(2 * Math.PI * 120 * i * T);
            x[i] = new Complex(S, 0);
        }
    }
    public static Complex[] dft(Complex[] x) {
        int n = x.length;

        if (n == 1)  // exp(-2pi*j) = cos(-2pi)+j * sin(-2pi) = 1
            return x;

        Complex[] result = new Complex[n];
        for (int i = 0; i < n; i++) {
            result[i] = new Complex();
            for (int k = 0; k < n; k++) {
                double p = -2 * k * Math.PI * i / n ;
                // 欧拉公式e^(-j (2pi * k * i) / N) = cos(-2pi * k * i / N) + i*sin(-2pi * k * i/ N)
                Complex e = new Complex(Math.cos(p), Math.sin(p));
                result[i] = result[i].plus(x[k].multiply(e));
            }
        }
        return result;
    }
    public static Complex[] fft(Complex[] x) {
        int n = x.length;
        if (n == 1)
            return x;

        // 信号数为奇数不满足对称性，使用dft计算
        if (n % 2 != 0)
            return dft(x);

        // 取下标为偶数的信号
        Complex[] even = new Complex[n / 2];
        for (int i = 0; i < n / 2; i++) {
            even[i] = x[2 * i];
        }
        Complex[] evenValue = fft(even);

        // 取下标为奇数的信号
        Complex[] odd = new Complex[n / 2];
        for (int i = 0; i < n / 2; i++) {
            odd[i] = x[2 * i + 1];
        }
        Complex[] oddValue = fft(odd);

        // 相加
        Complex[] result = new Complex[n];
        for (int i = 0; i < n / 2; i++) {
            double p = -2 * Math.PI * i / n ;
            Complex e = new Complex(Math.cos(p), Math.sin(p));
            result[i] = evenValue[i].plus(e.multiply(oddValue[i]));
            result[i + n / 2] = evenValue[i].minus(e.multiply(oddValue[i]));
        }
        return result;
    }
    public static void writeText(String filename,Complex[]result) {
        try {
            File writeName = new File(filename); // 相对路径，如果没有则要建立一个新文件
            writeName.createNewFile(); // 创建新文件,有同名的文件的话直接覆盖
            try (FileWriter writer = new FileWriter(writeName);
                 BufferedWriter out = new BufferedWriter(writer)
            ) {
                for (int i = 0; i < result.length; i++) {
                    out.write(result[i].toString()+"
"); // 
即为换行
                }
            }
        } catch (IOException e) {
            e.printStackTrace();
        }
        System.out.println("数据写入成功！");
    }

    public static void main(String[] args) {
        int length = 1500;
        Complex[] x = new Complex[length];
        Complex[] result;
        CreateSignal(length, x);

        long start1 = System.currentTimeMillis();
        result = dft(x);
        long end1 = System.currentTimeMillis();

        long start2 = System.currentTimeMillis();
        result = fft(x);
        long end2 = System.currentTimeMillis();


        System.out.println("FFT结果：");
        for (int i = 0; i < length; i++) {
            System.out.println("第"+(i+1)+"个数据："+result[i].toString());
        }
        System.out.println("------------------------------------------------");

        System.out.println("DFT运行时间: " + (end1 - start1) + "ms");
        System.out.println("FFT运行时间: " + (end2 - start2) + "ms");

        String filename = "C:\Users\xxx\Desktop\算法课程\xxx\shuju.txt";
        writeText(filename, result);

    }
}

结果

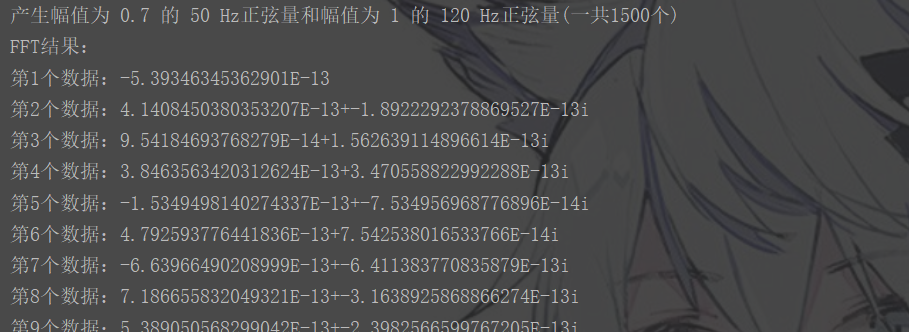
 验证（matlab）

clc
clear
close all;
Fs = 1000;                   
T = 1/Fs;             
L = 1500;          
t = (0:L-1)*T; 
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);

%matlab fft函数
Y = fft(S);
%导入java产生的数据
file = fopen('shuju.txt');
p = textscan(file,'%s');
pp =[str2double(p{:})]';

P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
subplot(1,2,1)
plot(f,P1) 
hold on;
title('FFT of Matlab')
xlabel('f (Hz)')
ylabel('|P1(f)|')

X2 = abs(pp/L);
X1 = X2(1:L/2+1);
X1(2:end-1) = 2*X1(2:end-1);
f1 = Fs*(0:(L/2))/L;
subplot(1,2,2);
plot(f1,X1) 
title('FFT of Java')
xlabel('f (Hz)')
ylabel('|X1(f)|')
hold off;

结果：