数据是如何在内存中存储的?
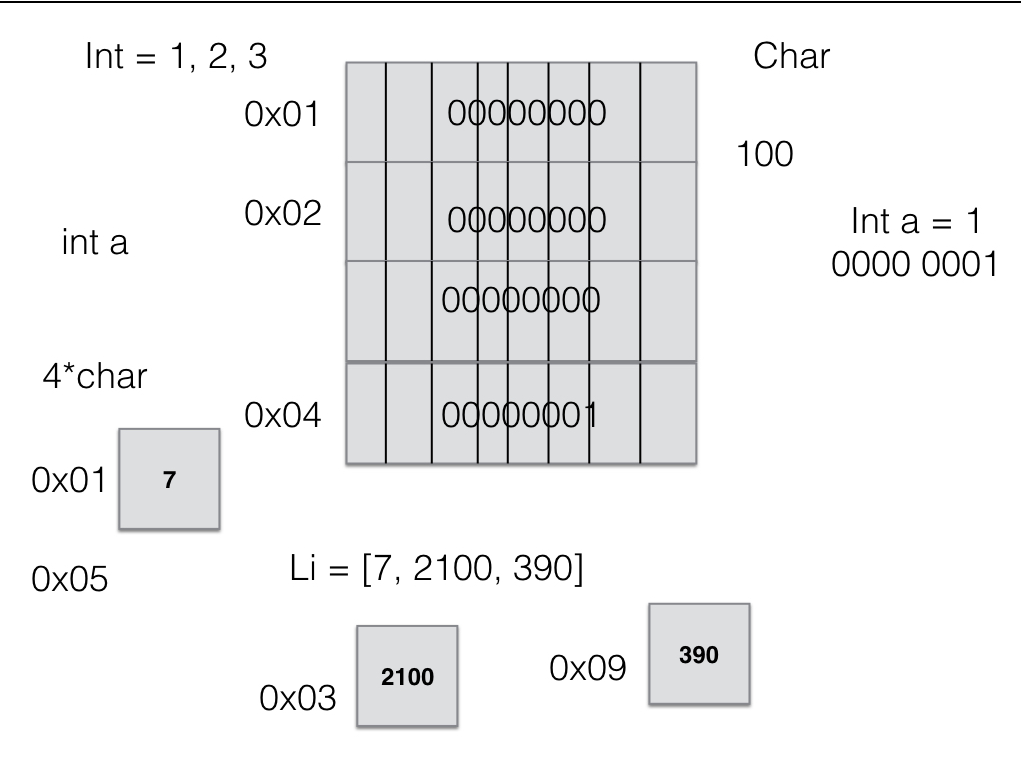
在32位的计算机上,1个字节有8位,内存寻址的最小单位就是字节。假设我们有一个int类型的值,它从0x10开始,一个int占据4个字节,则其结束于0x13。
那么数据类型有什么意义呢?
它确定了一个特定类型的数据到底要申请多大的内存地址来存储(大小),并且决定取到的二进制数应该如何解释(意义)。
地址里存储的只有二进制数,但对于数字和字符同一二进制数代表的意义是不同的。
同类型的数据在内存中是如何连续存储的?
假设有一个四个数的集合 24, 299, 10, 4,将它们连续地存储在一起时,在内存里的表现就像是它们紧挨着挤在一起。如果第一个元素从0x10开始,那整个集合就在0x25结束。每个元素都是内置在地址中的。代表集合的变量指向集合的开始地址0x10,要找到第一个元素就加上4。
因为类型相同,则每个元素的偏移量也相同,就可以有下图的公式(c就是元素类型的大小)。
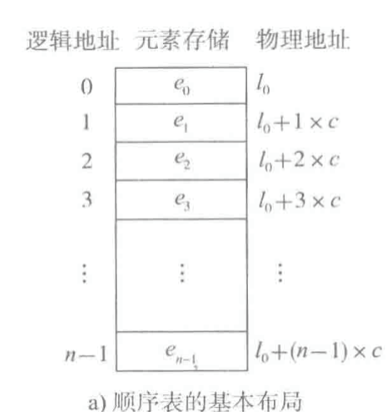
这也是为什么集合要从0开始了:元素下标表示的就是一个特定偏移量单位,第0个元素自然是没有任何偏移的。获得特定元素,也不需要遍历整个集合,计算偏移量即可。
不同类型的数据集合在内存中是如何存储的?
当不同的元素要挤在一个集合里时,用偏移量来定位就靠不住了,毕竟各自大小都不同。但不要忘了,内存地址本身的大小是固定的。
假设集合里有12, 1.24, 'ab' 三种不同的元素,它们的位置各不连续,分散在不同的地方。就申请一块3个元素大小的连续内存区域,里面每个元素都分别指向集合内的元素。
这时的元素是外置的。

顺序表在内存中的结构是什么?
要在内存中给集合开辟一块区域,总得先确定大小(容量),不然如何开辟?另外,确定区域后,还要知道当前已经占用了几个元素(元素个数),一旦溢出,就需要重新申请空间。
要表达这种结构,有两种实现方式。一种是把头信息和元素串到一起,形成一个元素个数+2的表。另一种就是把头信息和元素分开放,两者之间用一个元素建立一个链接,连在一起。

存储表信息的单元与元素存储区以连续的方式安排在一块存储区里,两部分数据的整体形成一个完整的顺序表对象。一体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的一部分,顺序表创建后,元素存储区就固定了。
分离式结构中表对象里只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另一个独立的元素存储区里,通过链接与基本表对象关联。
一旦表需要扩充,对于一体式结构来说,就要重新申请一块更大的空内存区域,将所有元素放入其中,再清空旧的内存区域。
对于分离式结构来说,则需要将链接地址更新一下,顺序表对象是不变的。
说到扩充,又是如何进行的呢?
采用分离式结构的顺序表,若将数据区更换为存储空间更大的区域,则可以在不改变表对象的前提下对其数据存储区进行了扩充,所有使用这个表的地方都不必修改。
扩充的策略可以说有两种。
每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。特点:节省空间,但是扩充操作频繁,操作次数多。
(就是以时间换空间,以后每次添加的元素过多就要多花时间重新扩容)
每次扩充容量加倍,如每次扩充增加一倍存储空间。特点:减少了扩充操作的执行次数,但可能会浪费空间资源。
(以空间换时间,每次扩容占用的空间大了,但扩容就可以少执行些)
说了以上这么多,这时我们就可以审视一下python中的list。
list有以下几个特点:
1.元素有位置下标,以索引就可以直接取到元素 --> 连续的存储空间,以偏移量计算取得元素,不必遍历所有元素
2.元素无论如何改变,表对象不变,也就是其id不变 --> 分离式结构,表头和元素内容分开储存,这样在更改list时,表对象始终是同一个,只是其指向的地址不同
3.元素可以是任意类型 --> 既要要求是连续存储,又可以存储不同类型的数据,那么其用的就是元素外置的方式,存储的只是地址的引用
4.可以任意添加新元素 --> 要能不断地添加新元素,其使用了动态扩充的策略
从实现上来讲,在python中创建空ist时,会申请一个8个元素大小的内存区域。以后如果满了,就扩容4倍,且当元素总数达到50000时,再扩容就改为2倍。
列表时间复杂度补充:
index() O(1)
append O(1)
pop() O(1)
pop(i) O(n)
insert(i,item) O(n)
del operator O(n)
iteration O(n)
contains(in) O(n)
get slice[x:y] O(k)
del slice O(n)
set slice O(n+k)
reverse O(n)
concatenate O(k)
sort O(nlogn)
multiply O(nk)