一,数的整除特性:
1,
一个数的末位能被2或5整除,这个数就能被2或5整除
一个数的两末位能被4或25整除,这个数就能被4或25整除
一个数的末三位能被8或125整除,这个数就能被8或125整除
以此类推
2,
一个数的各位数字之和能被3整除,这个数就能被3整除
一个数的各位数字之和能被9整除,这个数字就能被9整除
3,如果一个整数的奇位上的数字之和与偶位上的数字之和的差能被11整除,那么这个数就能被11整除
4,如果一个整数的末三位与末三位以前的数字组成的数之差能被7,11或13整除,那么这个数就能被7,11,13整除
二,约数与倍数问题(a如果能整除b,a称为b的倍数,b称为a的约数)
1,最大公约数(欧几里德—辗转相除):用大数除小数得余数,再用除数/余数循环直到能整除为之,最后一个除数就是最大公约数
那为什么可以用这种方法求得最大公约数呢:
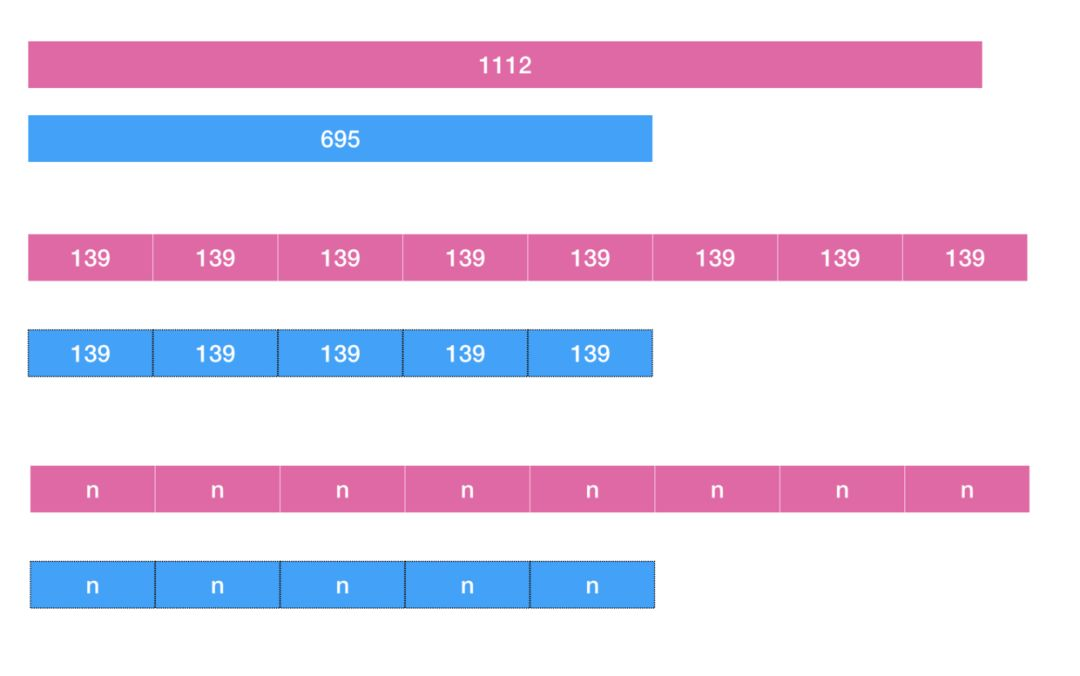
通过不停的求余数,从而找到最大情况下可以划分出的最大公约数N,N是上一个被求得的余数恰好可以被整除,所以得到了最合适的划分段N
2,互质数:公因数(公约数)只有1的两个非零自然数,叫做互质数
例如:9的因数有:1,3,9;10的因数有:1,2,5,10; //互质的两个数并不一定都是质数,例如9和10都是合数
3,最大公约数的性质:
几个数除以它们的最大公约数所得的几个商是互质数
4,求一个数所有的约数个数
用分解因数的形式表示:N=a1的p1次方*a2的p2次方*...*an的pn次方
那么所求的约数个数A=(p1+1)*(p2+1)*...*(pn+1)
例如504=2的3次方*3的2次方*7
那么它有(3+1)*(2+1)*(1+1)=24个约数
5,求一组分数的最大公约数:首先求出各分数的最小公倍数a,再求出各分子的最大公约数b,b/a即为最大公约数
6,求一组树的最小公倍数:待补充
三,余数问题
0,同余概念:所谓同余,就是几个数被一个数d除后有相同的余数,d称为模,例如a%d=c,b%d=c,那么就说a和b是模d同余的,数学记法为:a ≡ b (mod d),a和b除以d的余数是相等的
1,同余定理1:如果a,b除以c的余数相同,就称a,b对于除数c来说是同余的,且有a与b的差能被c整除,
例如,13%2=1,15%2=1,(15-13)%2=0
2,同余定理2:a与b的和除以c的余数,等于a,b分别除以c的余数之和(注意:当余数之和大于或等于除数时,应该将余数和再余一次除数)
公式表示:(a%c+b%c)%c=(a+b)%c
例如,23%5=3,19%5=4,余数和为7%5=2,(23+19)%5=2
3,同余定理3:a和b的乘积除以c的余数,等于a,b分别除以c的余数之积(注意:当余数之积大于等于除数时,应该将余数再余一次除数)
公式表示:(a*b)%c=((a%c)*(b%c))%c
例如:23%5=3,19%5=4,余数之积为12%5=2,所以(23*19)%5=2
4,中国剩余定理(这个名字有点奇怪,题和解答也有点奇怪)
问题是:x余3得2,x余5得3,x余7得2,求x
解法是:先构造三个数21,70,15,(15%7=1,70%3=1,21%5=1)
然后有一个规律15*x%7=x...
所以可得公式:70a+21b+15c
没搞懂的地方是:三个数相加不影响所得余数?????,有时间再看看,太麻烦了这个
四,完全平方数
0,一个数能表示成某个整数的平方,如例如1*1,2*2,3*3等,则1,4,9为完全平方数
性质1:完全平方数末尾只能是0,1,4,5,6,9
性质2:偶数的平方是4的倍数,奇数的平方是4的倍数+1
性质3:完全平方数的因数个数为奇数
待补充:
1,最小公倍数
2,中国剩余问题
3,整数拆分最大乘积问题