矩阵相关概念的物理意义

参考链接：

矩阵乘法的本质是什么？

条件数

病态矩阵与条件数（&& 与特征值和SVD的关系）

 

矩阵的物理意义：

https://blog.csdn.net/NightkidLi_911/article/details/38178533

https://blog.csdn.net/NightkidLi_911/article/details/38189347

---------------------------------------------------------------------------------------

1. 空间

1. 一般性定义

从拓扑空间开始，一步步往上加定义，可以形成很多空间。线形空间其实还是比较初级的，如果在里面定义了范数，就成了赋范线性空间。赋范线性空间满足完备性，就成了巴那赫空间；赋范线性空间中定义角度，就有了内积空间，内积空间再满足完备性，就得到希尔伯特空间。

空间有很多种。你要是去看某种空间的数学定义，大致都是“存在一个集合，在这个集合上定义某某概念，然后满足某些性质”，就可以被称为空间。

为什么要用“空间”来称呼一些这样的集合呢？

首先看一下我们生活在其中的的三维空间的一些最基本的特点。

1. 由很多（实际上是无穷多个）位置点组成；

2. 这些点之间存在相对的关系；

3. 可以在空间中定义长度、角度；

4. 这个空间可以容纳运动，这里我们所说的运动是从一个点到另一个点的移动（变换），而不是微积分意义上的“连续”性的运动。

不管是什么空间，都必须容纳和支持在其中发生的符合规则的运动（变换）。在空间中往往会存在一种相对应的变换，比如拓扑空间中有拓扑变换，线性空间中有线性变换，仿射空间有仿射变换等，这些变换都是对应空间中允许的运动形式。

因此，“空间”是容纳运动的一个对象集合，而“变换”规定了对应空间的运动。

那么某个特定的“空间”有两个基本问题需要理解：

1. 该空间是什么样的对象的集合？

2. 该空间的运动是如何表述的？

2. 线性空间

[摘自百度百科] 向量空间亦称线性空间。设V是一个非空集合，P是一个域。若：

1.在V中定义了一种运算，称为加法，即对V中任意两个元素α与β都按某一法则对应于V内惟一确定的一个元素α+β，称为α与β的和。 

2.在P与V的元素间定义了一种运算，称为纯量乘法(亦称数量乘法)，即对V中任意元素α和P中任意元素k，都按某一法则对应V内惟一确定的一个元素kα，称为k与α的积。

3. 加法与纯量乘法满足以下8个条件(此处略)，则称V为域P上的一个线性空间，或向量空间。

 

简单表述：线性空间是这样一种集合，其中任意两元素相加可构成此集合内的另一元素，任意元素与任意数（可以是实数也可以是复数，也可以是任意给定域中的元素）相乘后得到此集合内的另一元素。

 

线性空间是个空间，那么

1. 线性空间是什么样的对象的集合？（线性空间中对象有什么共同点？）

2. 线性空间中的运动是如何表述的？（线性变换如何表示？）

2.1 线性空间中的对象

线性空间中的任何一个对象，通过选取基和坐标的办法，都可以表达为向量的形式。

只要找到合适的基，用向量可以表示线性空间里任何一个对象。这里头大有文章，因为向量表面上只是一列数，但是其实由于它的有序性，所以除了这些数本身携带的信息之外，还可以在每个数的对应位置上携带信息。为什么在程序设计中数组最简单，却又威力无穷呢？根本原因就在于此。

另外举两个不那么平凡的例子：

Ex1. 最高次项不大于n次的多项式的全体构成一个线性空间，也就是说，这个线性空间中的每一个对象是一个多项式。如果以 $x_0, x_1, ..., x_n$ 为基，那么任何一个这样的多项式都可以表示为一组 $n + 1$ 维向量，其中每一个分量 $a_i$ 就是多项式中 $x_{i - 1}$ 项的系数。

基的选取方法有多种，只要所选取的那一组基线性无关即可。

这样看，泰勒展开中的每一个多项式中的 $x^i$ ，其实也是一个函数在函数空间的基， 而多项式的系数可以看做在该基下的坐标值。

EX2. 闭区间 [a, b] 上的n阶连续可微函数的全体，构成一个线性空间。也就是说，这个线性空间的每一个对象是一个连续函数。对于其中任何一个连续函数，根据魏尔斯特拉斯定理，一定可以找到最高次项不大于n的多项式函数，使之与该连续函数的差为0，也就是说，完全相等。这样就把问题归结为L1了。后面就不用再重复了。

2.2 线性空间中的运动及运动的表述

2.2.1 线性变换

线性空间中的运动，被称为线性变换。

线性变换的定义：设有一种变换T，使得对于线性空间V中任何两个不同的对象 x 和 y，以及任意实数 a 和 b， 有：$T(ax + by) = aT(x) + bT(y)$, 那么就称 $T$ 为线性变换。

线性变换的表示：在线性空间中，选定一组基后，不仅可以用一个向量来描述空间中的任何一个对象，而且可以用矩阵来描述该空间中的任何一个运动（变换）。而使某个对象发生对应运动的方法就是，用代表该运动的矩阵，乘以代表该对象的向量。

简而言之：在线性空间中选定基之后，向量刻画对象，矩阵刻画对象的运动，用矩阵与向量的乘法施加运动。

矩阵的本质是运动的描述。

注意：这里的运动不是涉及微积分的连续性的运动，而是瞬间性的变换。（连续性的运动举个例子，一只小猫从A点走到B点，需要走一定时间才可以达到。瞬间性的变换举个例子，量子在不同能量轨道上的跃迁。）矩阵变化显然是瞬间性的，故下文中，将“运动”一词替换成“变换”。

矩阵是线性空间里变换的描述。

在一个线性空间V里的一个线性变换T，当选定一组基之后，就可以表示为矩阵。

基：可以把基看做线性空间里的坐标系。

选定一组基：可以理解为选定一个坐标系。

那么矩阵可以理解为：

矩阵是线性空间中的线性变换的一个描述。在一个线性空间中，只要选定一组基，那么对于任何一个线性变换，都能用一个确定的矩阵来加以描述。

2.2.2 变换的描述 vs 变换

在2.2.1中需要区别“线性变换”和“线性变换的一个描述”这两个概念。

线性变换，指“变换”本身， 每个变换可能有多种“描述”的方式，都表示同一个“变换”。

举个例子：给一个物体拍照，物体就是这个对象本身；但通过变换不同的角度等，可以给它拍出来很多不同的照片，这些照片都是这个物体的“描述”，但照片并不是这个物体本身。

同样的，对于线性空间中的一个变换，选择不同组的基，可以得到不同的矩阵，来对这同一个变换进行描述。但这些矩阵并不是变换本身。

那么，如何不同的矩阵是否是对同一个变换的描述呢？

若矩阵A与B是同一个线性变换的两个不同的描述（之所以会不同，是因为选定了不同的基，也就是选定了不同的坐标系），则一定能找到一个非奇异矩阵P，使得A、B之间满足这样的关系：
$$ A = P^{-1} * B * P $$

那么，A, B互为相似矩阵。即，相似矩阵是对同一个线性变换的不同的描述矩阵。其中的矩阵P，就是A矩阵所基于的基 与B矩阵所基于的基，这两组基之间的一个变换关系。

2.2.3 对线性变换的两个视角

视角1：固定对象所处的坐标系，对象的变换等价于对象在该坐标系下的位置的变换。

　　　  同2.2.1与2.2.2所述：把矩阵看做是运动的描述，矩阵与向量相乘就是使向量（点）运动的过程。

　　　  EX1. $Ma = b ag1$ 表示：向量a经过矩阵M所描述的变换，变成了向量b。

视角2：固定对象的位置，对象的变换等价于坐标系的变换。

对于视角2：

矩阵可以看做是一组向量组成的。对于n维n阶非奇异的方阵（向量两两线性无关），那么可以将这组向量看做该线性空间的一组基，也相当于该空间的一个坐标系。

如何通过变换坐标系，实现线性变换呢？

举个例子，比如把点(1, 1)变到点(2, 3)去，点不动，变坐标系，让x轴的度量（单位向量）变成原来的1/2，让y轴的度量（单位向量）变成原先的1/3，这样点还是那个点，可是点的坐标就变成(2, 3)了。

EX2. $$Ma = b ag1$$

$$Ma = Ib ag2$$

(2)的物理意义是：有一个向量，在坐标系$M$的度量下的度量结果是$a$，那么它在坐标系 $I$ 的度量结果是向量 $b$. 这里 $I$ 表示单位矩阵。

(2) 表示，同样的向量，选择不同的坐标系，其表示方式不同。

以该视角看，矩阵乘法 $M cdot N$ 表示：声明了一个在 $M$ 坐标系中度量出的另一个坐标系 $N$, 而 $M$本身是在 $I$ 坐标系中度量出来的。

2.2.4 坐标系的变换

对于上面的例子，在M坐标系中表示为(1,1)的点，在I坐标系中表示为(2,3).

那么如果已知有一个点，在$I$坐标系中表示为(2,3)，那么该点在$M$坐标系中应该表示为什么呢？

这里需要将 $Ma = Ib ag2$ 转换为$Ia = Mb ag3$.如何实现这样的转换呢？将(2) 中的 $Ma$ 左乘 $M^{-1}$ 即M的逆矩阵。

这里，矩阵乘法表示的不是2.2.1和2.2.2中所表示的，“对向量施加变换”了，而是“对坐标系施加变换”。

那么对于矩阵乘法 $M cdot N$，

一方面可以认为是2.2.3中所述，声明了一个在 $M$ 坐标系中度量出的另一个坐标系 $N$, 而 $M$本身是在 $I$ 坐标系中度量出来的。从坐标系的角度看，可以这样理解：对N坐标系基的每一个向量，把它在I坐标系中的坐标找出来，然后汇成一个新的矩阵。

另一方面可以认为是2.2.4中所述，坐标系N在运动M下的变换结果。从变换的观点看，对坐标系N施加M变换，就是把组成坐标系N的每一个向量施加M变换。

3. 特征向量与特征值

特征向量表示：变换的方向；

特征值表示：变换的尺度。

4. 病态矩阵

4.1 病态矩阵的定义

解线性方程组Ax=b时，若对于系数矩阵A及右端项b的小扰动 δA、δb，方程组 (A+δA)χ=b+δb的解 χ 与原方程组Ax=b的解差别很大，则称矩阵A为病态矩阵。

举个例子：

4.2 条件数 -- 评价一个方程组是否为病态

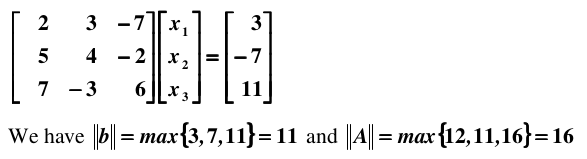
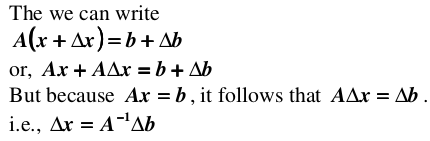
那么，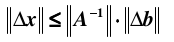

又因为，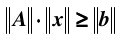

综合上面两式得，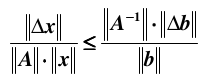

得到最终关系：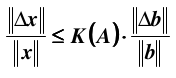

如果是矩阵A产生误差，同样可得：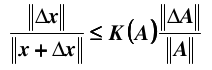

其中，条件数定义为：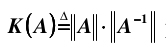

一般来说，方程组解集的精度大概是 个十进制的位的误差。 比如，IEEE 标准表示的双精度浮点数的有效位是 16 位，如果条件数是 1e+10, 那么得到的结果中只有 6 位是精确的。所以，只有当方程组是良态时，残差 R = Ax - b 才能准确指示解的精度。

4.3 病态的由来

比如线性方程组

〔1 2 [x = [4 　3.999 1] y] 7.999] 　的解是(x,y)=(2,1)

而 　〔1 2 [x = [4.001 　3.999 1] y] 7.998] 　的解是(x,y)=(-3.999,4.000)

可见b很小的扰动就引起了x很大的变化，这就是A矩阵条件数大的表现。一个极端的例子，当A奇异时，条件数为无穷，这时即使不改变b，x也可以改变。奇异的本质原因在于矩阵有0特征值，x在对应特征向量的方向上运动不改变Ax的值。如果一个特征值比其它特征值在数量级上小很多，x在对应特征向量方向上很大的移动才能产生b微小的变化，这就解释了为什么这个矩阵为什么会有大的条件数，事实上，正规阵在二范数下的条件数就可以表示成 abs(最大特征值/最小特征值)。

4.4 特征值

假设 A 的两个单位特征向量是 x1, x2, 根据特征向量的性质：

上述矩阵 A 的特征值和特征向量分别为：

对于平面上的某一个向量 b，可以分解为两个特征向量的线性组合：

把上式带入，

如果  远远大于 ， 当 b 点在 x1 方向发生移动, m 值改变， 解集 x 变化不明显， 反之， 如果在 x2 方向移动， n 值改变，解集 x 变化非常大 ！可以看到，特征值对解集起到了一个 scaling 的作用。反过来说，如果一个特征值比其它特征值在数量级上小很多，x在对应特征向量 (x2) 方向上很大的移动才能产生b微小的变化.

4.5 SVD 

SVD 分解：

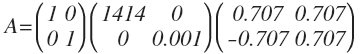
通过SVD ，将 A 分解成三个矩阵的乘积，中间的对角线矩阵也起到了 scaling 的作用。我们按照正向思维来考虑这个问题，现在来了一个解集 x 向量，左乘 A 矩阵等价与左乘 USV^T, x 向量正好等于 V^T 最后一行向量，经过 S 矩阵的 scaling 缩小之后对 b 的影响非常小。也就是说， 解集 x 在 V^T 最后一行的行向量方向自由度最大！自由度越大，越不稳定，极端情况是该方向奇异值为 0, 解集可以在该方向取任意值，这也正好对应了矩阵 A 有零特征值， Ax 在对应特征向量的方向上移动不改变 Ax 的值。

在不同的 norm 下，条件数又可以由最大奇异值与最小奇异值之间的比值，或者最大特征值和最小特征值之间比值的绝对值来表示，详情请参考维基百科

最后， A 的条件数究竟等于多少呢？ cond(A) = 2e+06

4.6 病态矩阵处理方法

真正的自由是建立在规范的基础上的。病态矩阵解集的不稳定性是由于解集空间包含了自由度过大的方向，解决这个问题的关键就是将这些方向去掉，而保留 scaling 较大的方向，从而把解集局限在一个较小的区域内。在上面的讨论中， A 矩阵的特征向量不一定正交，不适合做新基， SVD 分解正好分解出了正交基，可以选前 k 个 v^T 向量作为正交基。

比如，现在只选取前一个 (0.707, 0.707) 方向作为基，解集局限在 y = x 这条直线上。直观的解释就是， A 矩阵的两个列向量过于类似，我们就可以将它们等同看待，第一次 b = (1000, 0), 解集是(0.5, 0.5), 第二次 b = (1000, 0.001), 解集还是 (0.5, 0.5).

总结起来，解决 A 病态就是将解集限定在一组正交基空间内，即对于坐标 y， 选择 k 个正交基 Zk，解决问题：

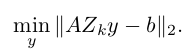
这个就是 reduce-rank model. 具体方法有 truncated SVD 和 Krylov subspace method。