Outline
使用逼近器的特点:
较少数量的参数表达复杂的函数 (计算复杂度)
对一个权重的调整可以影响到很多的点 (泛化能力)
多种特征表示和逼近器结构 (多样性)
激活函数
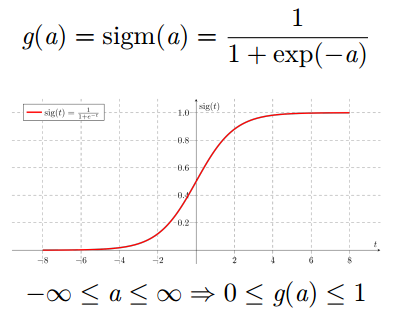
Sigmoid 激活函数
将神经元的输出压缩在 0 和 1 之间
永远都是正数
有界
严格递增
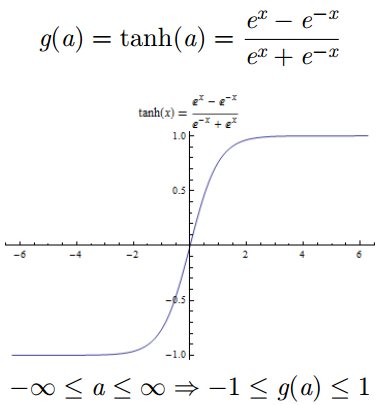
tanh 双曲正切函数
将神经元的输出压缩在
-1 和 1 之间
有正有负
有界
严格递增
线性整流 (Rectified Linear Unit, ReLU) 激活函数
以 0 作为下界 (永远都是非负的)
容易让神经元产生稀疏的激活行为
无上界
严格递增
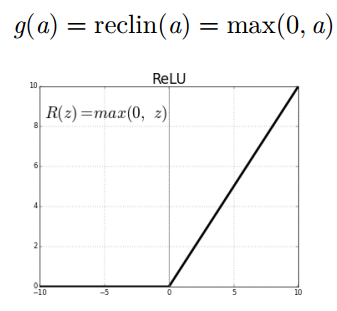
通用近似定理 (Hornik, 1991)
“如果一个前馈神经网络具有线性输出层和至少一层隐藏层, 只要给予网络足够数量的神经元,便可以实现以足够高精度来逼近任意一个在 Rn 的紧子集 (Compact subset) 上的连续函数。 ”
定理适用于 sigmoid, tanh, 和其它激活函数
但是定理并不代表一定存在某个学习算法, 能够找到具有满足近似性能的参数
置信风险: 分类器对 未知样本进行分类,得到的误差。
经验风险: 训练好的分类器,对训练样本重新分类得到的误差。即样本误差
结构风险:置信风险 + 经验风险
小批量 Mini-batch 梯度下降
更新是基于一组小批量的样本 {(x(i:i+b); y(i:i+b))}(不再是单 一样本)
梯度对应于正则化损失在小批量样本上的平均
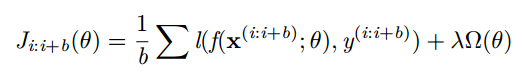
可以得到对梯度更加精确的估计
可以使用矩阵运算, 计算效率更高

在训练集 Dtrain上训练你的模型
在验证集 Dvalid上选择模型
-----包括选择超参; 隐含层尺寸; 学习率; 迭代/训练次数; 等等
在测试集 Dtext上评估泛化能力
泛化的含义是模型在未见过的样本上的表现
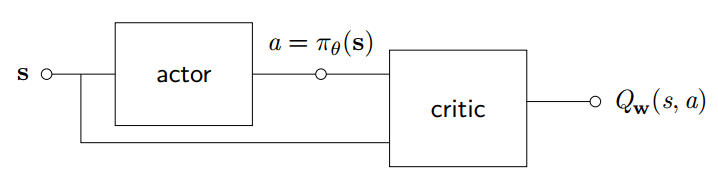
确定性 Actor-Critic
对于确定性策略, 可以使用神经网络逼近器构建 actor, 直接输出策略确定性的动作

设计另一个神经网络构造 Critic 用于逼近 Q 函数
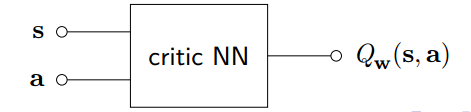
对 Critic NN 可以使用例如 TD 学习算法训练网络权重
对 Actor NN 希望能够输出最优动作使得 Q 函数最大化
![]()
