AUC(Area under curve)是机器学习常用的二分类评测手段,直接含义是ROC曲线下的面积, 对于二分类模型,还有很多其他评价指标,比如 logloss,accuracy,precision。如果你经常关注数据挖掘比赛,比如 kaggle,那你会发现 AUC 和 logloss 基本是最常见的模型评价指标。
-
AUC = 1,是完美分类器;
-
AUC = [0.85, 0.95], 效果很好;
-
AUC = [0.7, 0.85], 效果一般;
-
AUC = [0.5, 0.7], 效果较低,但用于预测股票已经很不错了;
-
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值;
-
AUC < 0.5,比随机猜测还差。
为什么 AUC 和 logloss 比 accuracy 更常用呢?
因为很多机器学习的模型对分类问题的预测结果都是概率,如果要计算 accuracy,需要先把概率转化成类别,这就需要手动设置一个阈值,如果对一个样本的预测概率高于这个预测,就把这个样本放进一个类别里面,低于这个阈值,放进另一个类别里面。
所以这个阈值很大程度上影响了 accuracy 的计算。使用 AUC 或者 logloss 可以避免把预测概率转换成类别。
如何计算
ROC曲线下面积:
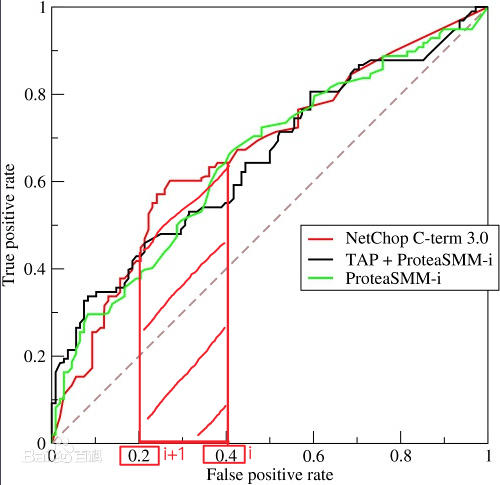
横坐标正是 FPR (False Positive Rate),纵坐标是 TPR (True Positive Rate),计算公式:
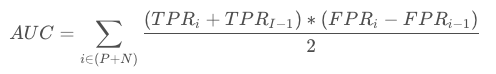
(梯形面积计算:上底+下底的合 * 高 /2,例如上图中的某个i下对应的面积)
由此引出True Positive Rate(真阳率)、False Positive(伪阳率)两个概念:
- TPRate的意义是所有真实类别为1的样本中,预测类别为1的比例。
- FPRate的意义是所有真实类别为0的样本中,预测类别为1的比例。
相关指标:
实际1,预测1:真正类(tp)
实际1,预测0:假负类(fn)
实际0,预测1:假正类(fp)
实际0,预测0:真负类(tn)
真实负样本总数=n=fp+tn
真实正样本总数=p=tp+fn
概率角度:
AUC 考虑的是样本的排序质量,它与排序误差有密切关系,在此,AUC可以在一定程度上理解为正样本排在负样本前面的概率,可得到计算公式:
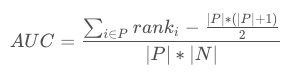
其中,rank 为样本排序位置从 1 开始,∣P∣ 为正样本数,∣N∣ 为负样本数。
对该公式的解释:
举个例子:这里,我们将所有样本得到的值从小到大排列(这个不必特别强调升序降序,主要看rank怎么定义==> 小的probs具有小的rank值),rank我们定义为样本在这个排序序列中的index。
| probs | rank | label |
| 0.1 | 1 | 0 |
| 0.2 | 2 | 0 |
| 0.5 | 3 | 0 |
| 0.6 | 4 | 1 |
| 0.7 | 5 | 0 |
| 0.8 | 6 |
1 |
| 0.9 | 7 | 1 |
这里,probs为预测得到的概率,P(正例个数,即原本label=1的样本个数) 为3,N(负例个数,即原本label=0的样本个数)为4。
我们要求的是AUC正例的rank比负例的rank大的概率,即P(rank正>rank负)。对于P个正例、N个负例,共有P*N(12)对(正例,负例)的组合对,我们要求AUC,需要求的是在所有组合对中,Rank正例大于Rank负例的比例是多少
我们看上表标红的正例:
对于rank为7的正例,共有rank-P个 rank正大于rank负的组合对:
rank7: (7, 7) (7,6) (7,5) (7,4) (7,3) (7,2) (7,1) : rank7 - P = 4
以此类推:
rank6:rank6-P+1 = 6-3+1 = 4
rank4:rank4-P+2 = 4-3+2 = 3
最后求得AUC = 正例rank大于负例的组合对/所有组合对 = 4 + 4 + 3 / 12 = 0.9167
观察可得,我们把ranki的部分加和加和就得到了公式中的![]() ,把后面减去的1, 2.....P(等差数列)加和就得到了公式中的
,把后面减去的1, 2.....P(等差数列)加和就得到了公式中的![]() 。
。
AUC的优点
它不受类别不平衡问题的影响,不同的样本比例不会影响AUC的评测结果。
- 例如在反欺诈场景,设欺诈类样本为正例,正例占比很少(假设0.1%),如果使用准确率评估,把所有的样本预测为负例,便可以获得99.9%的准确率。
- 但是如果使用AUC,把所有样本预测为负例,TPRate和FPRate同时为0(没有Positive),(0,0) 与 (1,1)连接,得出AUC仅为0.5,成功规避了样本不均匀带来的问题。
在训练时,可以直接使用AUC作为损失函数。
AUC指标本身和模型预测 score 绝对值无关,只关注排序效果,因此特别适合排序业务。
在python中,可直接调用sklearn中计算auc的方法~