条件:
1.每个顶点出现且只出现一次。
2.若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
一般用有向边指示顺序关系,运用于顺序关系。
例如,下面这个图:
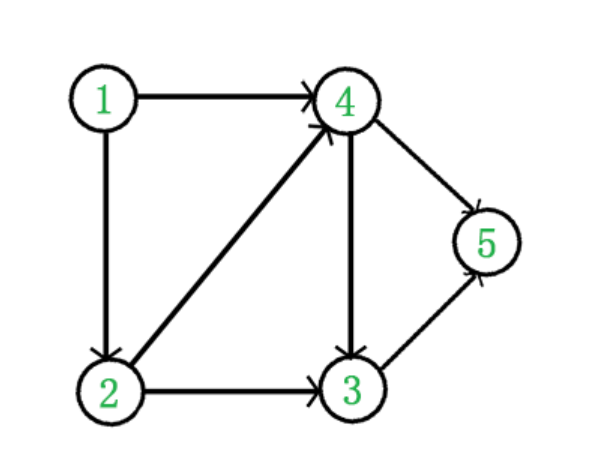
显然是一个DAG图,1→4表示4的入度+1,4是1的邻接点,
代码表示:前者deg[4]++;后者用vector[1].push(4)
如何写出拓扑排序代码?
1.首先将边与边的关系确定,建立好入度表和邻接表。
2.从入度为0的点开始删除,如上图显然是1的入度为0,先删除。
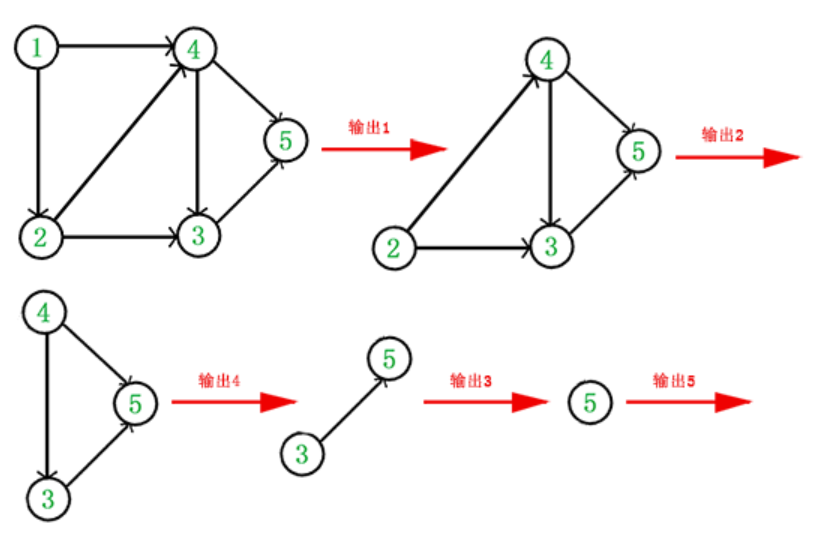
3.于是,得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。通常,一个有向无环图可以有一个或多个拓扑排序序列。因为同一入度级别的点可以有不同的排序方式。
4.拓扑排序可以判断图中有无环,如下图
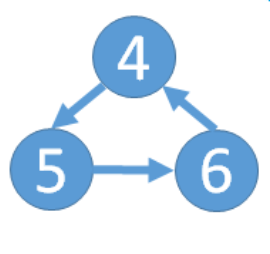
显然4,5,6入度都是1,不存在入度为0的点,无法进行删除操作。判断有无环的方法,对入度数组遍历,如果有的点入度不为0,则表明有环。
例题+代码
拓扑排序(一)-Hiho-Coder1174
描述
由于今天上课的老师讲的特别无聊,小Hi和小Ho偷偷地聊了起来。
小Ho:小Hi,你这学期有选什么课么?
小Hi:挺多的,比如XXX1,XXX2还有XXX3。本来想选YYY2的,但是好像没有先选过YYY1,不能选YYY2。
小Ho:先修课程真是个麻烦的东西呢。
小Hi:没错呢。好多课程都有先修课程,每次选课之前都得先查查有没有先修。教务公布的先修课程记录都是好多年前的,不但有重复的信息,好像很多都不正确了。
小Ho:课程太多了,教务也没法整理吧。他们也没法一个一个确认有没有写错。
小Hi:这不正是轮到小Ho你出马的时候了么!
小Ho:哎??
我们都知道大学的课程是可以自己选择的,每一个学期可以自由选择打算学习的课程。唯一限制我们选课是一些课程之间的顺序关系:有的难度很大的课程可能会有一些前置课程的要求。比如课程A是课程B的前置课程,则要求先学习完A课程,才可以选择B课程。大学的教务收集了所有课程的顺序关系,但由于系统故障,可能有一些信息出现了错误。现在小Ho把信息都告诉你,请你帮小Ho判断一下这些信息是否有误。错误的信息主要是指出现了"课程A是课程B的前置课程,同时课程B也是课程A的前置课程"这样的情况。当然"课程A是课程B的前置课程,课程B是课程C的前置课程,课程C是课程A的前置课程"这类也是错误的。
输入
第1行:1个整数T,表示数据的组数T(1 <= T <= 5)
接下来T组数据按照以下格式:
第1行:2个整数,N,M。N表示课程总数量,课程编号为1..N。M表示顺序关系的数量。1 <= N <= 100,000. 1 <= M <= 500,000
第2..M+1行:每行2个整数,A,B。表示课程A是课程B的前置课程。
输出
第1..T行:每行1个字符串,若该组信息无误,输出"Correct",若该组信息有误,输出"Wrong"。
Sample Input
2 2 2 1 2 2 1 3 2 1 2 1 3
Sample Output
Wrong Correct
#include<stdio.h> #include<algorithm> #include<iostream> #include<vector> #include<stack> #include<queue> #include<cstring> using namespace std; const int maxa=100100; vector<int>vec[maxa]; queue<int>q; int rudu[maxa]; int t,n,m,x,y,now; bool tuopu(){ int cnt=0; while(!q.empty()) q.pop(); for(int i=1;i<=n;i++) if(rudu[i]==0) q.push(i); while(!q.empty()){ now=q.front(); cnt++; q.pop(); for(size_t i=0;i<vec[now].size();i++) if(--rudu[vec[now][i]]==0) q.push(vec[now][i]); } if(cnt==n) return true; else return false; } int main(){ cin>>t; while(t--) { cin>>n>>m; memset(rudu,0,sizeof(rudu)); for(int i=1;i<=n;i++) vec[i].clear(); while(m--) { cin>>x>>y; vec[x].push_back(y); rudu[y]++;//入度+1 } if(tuopu()) cout<<"Correct"<<endl; else cout<<"Wrong"<<endl; } return 0; }