线性回归算法的衡量标准
- 均方误差(Mean Squared Error)
[frac{1}{m}sum_{i=1}^{m}(y_{test}^{(i)}- hat y{_{test}^{(i)}})^2
]
- 均方根误差(Root Mean Squared Error)
[sqrt{frac{1}{m}sum_{i=1}^{m}(y_{test}^{(i)}- hat y{_{test}^{(i)}})^2}
]
- 平均绝对误差(Mean Absolute Error)
[frac{1}{m}sum_{i=1}^{m} left | (y_{test}^{(i)}- hat y{_{test}^{(i)}})
ight|
]
加载波士顿房产数据
import numpy
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
# 打印此数据集的描述
print(boston.DESCR)

x = boston.data[:,5] #只取房间数量这个特征

plt.scatter(x,y)
plt.show()
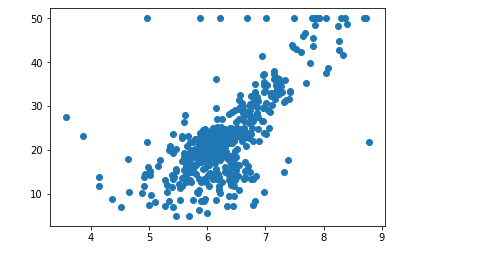
存在边缘极值点,用numpy中的"fancy index"去除数据中的上限值
x = x[y<50]
y = y[y<50]
plt.scatter(x,y)
plt.show()

from mylib.model_selection import train_test_split
from mylib.SimpleLineRegression import SimpleLineRegression
x_train,x_test,y_train,y_test = train_test_split(x,y,seed =666)
reg = SimpleLineRegression()
reg.fit(x_train,y_train)
y_predict = reg.predict(x_test)
通过训练,得到了a,b两个参数,从而确定了线性方程
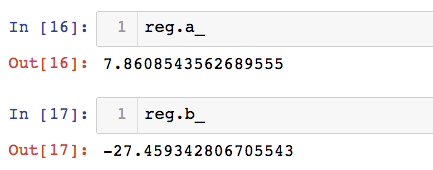
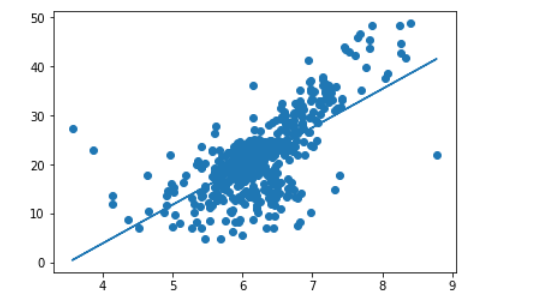
plt.scatter(x,y)
plt.plot(x,reg.predict(x))
plt.show()
MSE 均方误差
mse_test = numpy.sum((y_predict-y_test)**2) / len(x_test)
RMSE 均方根误差
import math
mse_test = numpy.sum((y_predict-y_test)**2) / len(x_test)
rmse_test = math.sqrt(mse_test)
MAE 平均绝对误差
mae_test = numpy.sum(numpy.absolute(y_predict-y_test)) / len(x_test) #absolute 求绝对值
上述算法指标封装为库:
metrics文件:
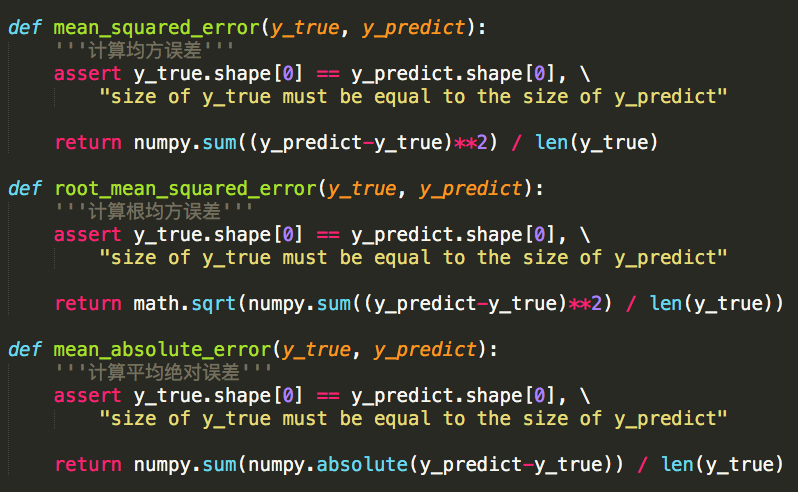
调用封装的算法度量库:
from mylib.metrics import mean_squared_error,root_mean_squared_error,mean_absolute_error
mean_squared_error(y_predict,y_test)
root_mean_squared_error(y_predict,y_test)
mean_absolute_error(y_predict,y_test)
sk-learn 中的MSE和MAE调用:###
from sklearn.metrics import mean_squared_error,mean_absolute_error
mean_squared_error(y_predict,y_test)
mean_absolute_error(y_predict,y_test)
R Squared
**表达式为: $ R^2 = 1 - frac{Sigma(hat{y}^{(i)} - y{(i)})2}{Sigma(overline{y}^{(i)} - y{(i)})2 } = 1 - frac{MSE(hat{y},y)}{Var(y)} $ **
- $ Sigma(hat{y}^{(i)} - y{(i)})2 = SS_{residual} $ 使用得到的模型预测产生的错误
- $ Sigma(overline{y}^{(i)} - y{(i)})2 = SS_{total} $ 使用(y=hat{y})预测产生的错误(baseline Model)

# var求方差
R2 = 1 - mean_squared_error(y_test,y_predict)/numpy.var(y_test)
封装到mylib中的metrics库中
from mylib.metrics import r2_score
r2_score(y_test,y_predict)
# 在线性回归类中封装score方法
reg.score(x_test,y_test)