scikit-learn中的逻辑回归
构造数据集
import numpy
import matplotlib.pyplot as plt
numpy.random.seed(666)
X = numpy.random.normal(0,1,size=(200,2))
# 决策边界为二次函数
y = numpy.array(X[:,0]**2 + X[:,1] < 1.5,dtype='int')
# 随机改变20个点,目的是添加噪点
for _ in range(20):
y[numpy.random.randint(200)] = 1
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

用scikit-learn中的逻辑回归:
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly',PolynomialFeatures(degree=degree)),
('stand_scalor',StandardScaler()),
('log_reg',LogisticRegression())
])
x_train,x_test,y_train,y_test = train_test_split(X,y)
当多项式为2阶时
poly_log_reg = PolynomialLogisticRegression(2)
poly_log_reg.fit(x_train,y_train)
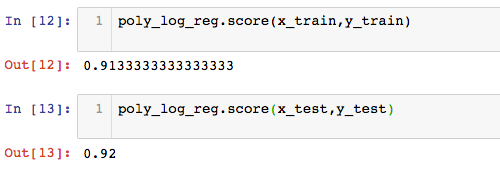
算法准确率为92%
绘制决策边界(决策边界绘制方法见上篇):

当多项式为20阶时:
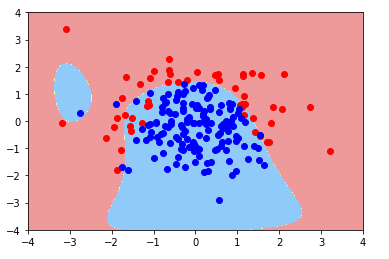
可以看出,随着多项式项的增加,模型变得过拟合了
改变模型正则化的参数
scikit-learn中使用正则化的方称为:(Ccdot J( heta )+L1/L2),其中默认系数C为1,正则化项为L2
- 减小系数C,增大正则化项的比例
def PolynomialLogisticRegression(degree,penalty='l2',C=1):
return Pipeline([
('poly',PolynomialFeatures(degree=degree)),
('stand_scalor',StandardScaler()),
('log_reg',LogisticRegression(penalty=penalty,C=C))
])
poly_log_reg2 = PolynomialLogisticRegression(20,penalty='l2',C=0.1)
poly_log_reg2.fit(x_train,y_train)

- 改变正则项L2为L1
poly_log_reg3 = PolynomialLogisticRegression(20,penalty='l1',C=0.1)
poly_log_reg3.fit(x_train,y_train)
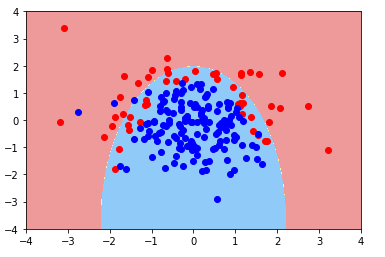
注:scikit-learn中的逻辑回归中,损失函数系数C,多项式阶数,正则化项等都是算法的超参数,在具体的应用中,需要使用网格搜索,得到最合适的参数组合。