题目大意
(i)和(j)是树上不同的两个点,计算下面公式的值
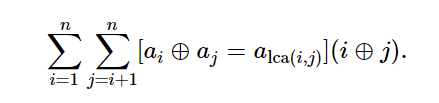
解题思路1(点分治)
如果用点分治的话,很容易想到可以把重心当(lca)来计算子树间的贡献。因为题目是有根树,所以在点分治的过程中,可能会有某个子树的父子关系是颠倒的,不过对于点分治以重心(u)为根的子树来说,这种子树只会有一个,那么对于其他子树来说就正常计数,而对于深度比(u)小的那个点(v)来说,其子树中深度比(v)大的点和(u)的(lca)就是(v),而深度比(v)更小的点就和(u)与(v)的关系是类似的,递归求解即可。
因为计算的是节点编号之和,不好直接处理,所以可以采用拆位的方式,将每个编号的二进制位拆开,用(cnt[val[u]][20])来表示值为(val[u])的所有编号的每个二进制位一共有多少1,计数的时候因为我们的(lca)已经事先知道了,所以对于每个子树的节点来说其对应的另一个值就是(val[lca] xor val[u]),用其对应的二进制位0和1的数量来计算就行了。
const int maxn = 2e6+10;
const int maxm = 1e6+10;
vector<int> e[maxn];
int sz[maxn], mx[maxn], cnt[maxn][20];
int rt, val[maxn], vis[maxn], tsz[maxn];
vector<int> res, tmp;
ll ans = 0;
int d[maxn];
void get_dis(int u, int p) {
for (auto v : e[u]) {
if (v==p) continue;
d[v] = d[u]+1;
get_dis(v, u);
}
}
void get_rt(int u, int p, int szr) {
sz[u] = 1, mx[u] = 0;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
get_rt(v, u, szr);
sz[u] += sz[v];
if (sz[v]>mx[u]) mx[u] = sz[u];
}
if (szr-sz[u]>mx[u]) mx[u] = szr-sz[u];
if (!rt || mx[u]<mx[rt]) rt = u;
}
void solve1(int u, int p, int x) {
res.push_back(val[u]);
tmp.push_back(u);
for (int i = 0; i<20; ++i) {
int t = u>>i&1;
if (t) ans += (1LL<<i)*(tsz[val[u]^x]-cnt[val[u]^x][i]);
else ans += (1LL<<i)*cnt[val[u]^x][i];
}
//cout << u << ' ' << ans << endl;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
solve1(v, u, x);
}
}
void solve2(int u, int p, int x) {
int t = -1;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
if (d[v]<d[u]) {
t = v;
continue;
}
solve1(v, u, x);
}
if (t!=-1) solve2(t, u, val[t]);
}
void calc(int u) {
int t = -1;
for (auto v : e[u]) {
if (vis[v]) continue;
if (d[v]<d[u]) {
t = v;
continue;
}
solve1(v, u, val[u]);
for (auto num : tmp) {
++tsz[val[num]];
for (int i = 0; i<20; ++i)
if (num>>i&1) ++cnt[val[num]][i];
}
tmp.clear();
}
if (t!=-1) {
++tsz[val[u]];
res.push_back(val[u]);
for (int i = 0; i<20; ++i)
if (u>>i&1) {
++cnt[val[u]][i];
}
solve2(t, u, val[t]);
}
for (auto v : res)
for (int i = 0; i<20; ++i) cnt[v][i] = 0, tsz[v] = 0;
tmp.clear();
res.clear();
}
void div(int u) {
//cout << u << endl;
vis[u] = 1;
calc(u);
for (auto v : e[u]) {
if (vis[v]) continue;
rt = 0; sz[rt] = INF;
int t = sz[v];
get_rt(v, -1, t);
get_rt(rt, -1, t);
div(rt);
}
}
int main() {
IOS;
int n; cin >> n;
for (int i = 1; i<=n; ++i) cin >> val[i];
for (int i = 1; i<n; ++i) {
int a, b; cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
rt = 0, sz[rt] = INF;
d[1] = 1;
get_dis(1, 0);
get_rt(1, -1, n);
get_rt(rt, -1, n);
div(rt);
cout << ans << endl;
return 0;
}
解题思路2(dsu on tree)
很容易想到(n^2)的做法,在dfs过程中,每个节点(u)的不同子树之间的(lca)就是(u)自己,所以可以写一个(n^2)的暴力每到一个点就计算一下不同子树之间的贡献,计算方法还是之前拆位的思路。
如何优化呢?之前的做法每回溯到一个新的点就需要对子树信息清空,然后再重新计算子树贡献,但是我们可以发现,对于(u)来说,他的第一个儿子的信息是可以保留的,这时候如果我们保留的是一个重儿子,然后再把其他的轻儿子的子树信息合并到重儿子上,就能把时间复杂度优化到(nlog(n))了(类似树剖)。
const int maxn = 2e5+10;
const int maxm = 2e6+10;
int n, val[maxn];
vector<int> e[maxn];
int sz[maxn], mx[maxn];
void dfs(int u, int p) {
sz[u] = 1; //求重儿子
for (auto v : e[u]) {
if (v==p) continue;
dfs(v, u);
sz[u] += sz[v];
if (sz[mx[u]]<sz[v]) mx[u] = v;
}
}
int flag, cnt[maxm][20], num[maxm]; ll ans;
void count(int u, int p, int x, int f) {
if (f==0) { //f = 0,计算贡献
for (int i = 0; i<20; ++i) {
if (u>>i&1) ans += (1LL<<i)*(num[x^val[u]]-cnt[x^val[u]][i]);
else ans += (1LL<<i)*cnt[x^val[u]][i];
}
}
else { //f = 1 or -1,加上or删除贡献
num[val[u]] += f;
for (int i = 0; i<20; ++i)
if (u>>i&1) cnt[val[u]][i] += f;
}
for (auto v : e[u]) {
if (v==p || v==flag) continue; //之前计算的重儿子信息保留了,不再计算
count(v, u, x, f);
}
}
void dsu(int u, int p, bool keep) {
for (auto v : e[u]) {
if (v==p || v==mx[u]) continue;
dsu(v, u, 0); //先计算轻儿子
}
if (mx[u]) { //有重儿子就计算并保留信息
dsu(mx[u], u, 1);
flag = mx[u];
}
++num[val[u]]; //加上当前节点的信息,因为没有$u$是$v$的$lca%,俩值异或还等于$u$自己的情况(没有为0的值)
for (int i = 0; i<20; ++i)
if (u>>i&1) ++cnt[val[u]][i];
for (auto v : e[u]) {
if (v==p || v==flag) continue;
count(v, u, val[u], 0);
count(v, u, val[u], 1);
}
flag = 0;
if (!keep) count(u, p, val[u], -1); //如果当前节点不是父亲节点的重儿子,删除贡献
}
int main() {
IOS;
cin >> n;
for (int i = 1; i<=n; ++i) cin >> val[i];
for (int i = 1; i<n; ++i) {
int a, b; cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dfs(1, 0);
dsu(1, 0, 0);
cout << ans << endl;
return 0;
}