这里是学了两遍LCT,又忘了两遍的shzr。
今天让我们再来学一遍LCT;这次我写了笔记,以后忘了就看看笔记,不用花那么多时间了。
首先来稍微复习一下LCT的一些基本知识:
·LCT用来维护森林;
·一棵LCT由多棵Splay组成,每棵Splay里的点是树上的一段路径。具体来说,是树上一段"祖先-子孙"路径。同时,每个树上的点会且只会出现在一个Splay中;
·中序遍历每个Splay,得到的点的深度序列是递增的;
·森林中的边被分为两类:虚边和实边;这两类边在LCT中不一定真的出现,但是都会有体现:对于按照Splay中序遍历得到的点序列,相邻两点间的边就是实边;每个Splay还有一个总的"祖先",从这个Splay中深度最小的点到这个"祖先"之间存在一条虚边;不要错误的以为成Splay的根到那个"祖先"的边,因为Splay的根是随意的;
接着来学习各种基本操作:
$ m Access(x)$
值得注意的是,虚实边的划分并没有什么原理,其实是可以随便划分的;
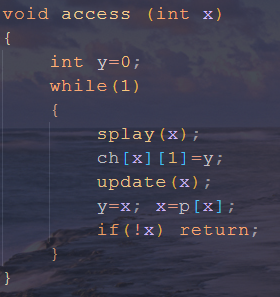
$assess(x)$ 这个操作就是指:将森林中 $x$ 到树根的这条链全部变实,同时 $x$ 变为这条实链中深度最大的点(不再有实儿子);
其实方法是很简单的...首先将 $x$ 旋转到所在Splay的根,然后断掉 $x$ 的右儿子,连上上一次循环时的 $x$(因为 $x$ 应该是深度最大的),不停地重复这三步,直到 $x$ 和根到达同一个Splay里,就完成了,是不是很简单呀~
不过Splay一般是要维护一些信息的,所以在断右儿子,改右儿子的时候都不要忘了 $ m pushup$ 呀;
什么?你说 $ m pushdown$ 怎么处理?事实上不用管,因为在改儿子的时候显然不会还有标记;
$ m Makeroot(x)$
就是把 $x$ 换到根上啦~
其实这利用了一个性质:将 $x$ 变成新根前后,父亲/儿子出现变化的点只会是 $x$ 到原根路径上的那些点;所以,我们首先 $ m Access(x)$ ,然后 $ m Splay(x)$,这样以后 $x$ 就会没有右儿子,在这里打一个翻转标记,翻转这条链就好啦~

$ m Findroot(x)$
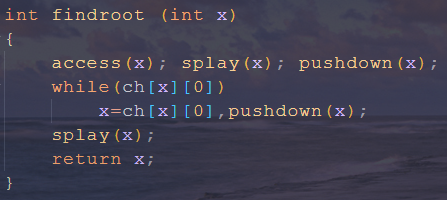
就是找到 $x$ 所在的根啦。首先 $ m Makeroot(x)$,然后一路往左走就找到了~
$ m Split(x,y)$
这个操作的意思是把 $x,y$ 弄到一条链上。方法很简单,$ m Makeroot(x)+Access(y)+Splay(y)$ 就OK了;
$ m Link(x,y)$
就是连边啦~ $ m Makeroot(x)+(f[x]=y)$ 就好啦;
$ m Cut(x,y)$
就是断边啦~ $ m split(x,y)+(f[x]=0,ch[y][0]=0)$ 就好啦;
如果断边不一定合法怎么办呢?开个Map记录有哪些边是存在的。好像很有道理的样子...还有另一种方法,这里也介绍一下吧;
首先判断两个点是否联通(显然);方法是 $ m Makeroot(x)+findroot(y)$ ;不要忘了 $ m findroot$ 里是含有 $ m access$ 的呀~
如果联通,那么现在我们就得到了一个以 $y$ 为根的Splay,此时,必须满足 $ m f[x]=y,ch[y][0]=x$ 才有可能存在这条边。为什么说可能呢?因为如果 $ m ch[x][1]!=0$,那么就说明 $ m x,y$ 间还有其他的点了。(注意Splay里的边并不能代替原树里的边啊!)
$ m Tips$:
还有一个需要注意的小细节:Splay时必须从上往下放标记,也就是在Splay以前,先访问整条根路径,放完标记再旋转;什么,你说为什么普通Splay不用这样?其实吧......普通Splay也是需要这样的,不过一般我们可能会先来一个找第K大之类的操作,等到splay时根本就没有标记可放了,所以怎么写都对...
最后说句闲话,我的IDE是不是挺好看的(逃
---shzr