树状数组
学之前感觉这是个非常非常难的数据结构,学完才发现也没有想象中那么难,但是题可以出的非常难。
这里就有一些同学坚持认为树状数组没有用,其实树状数组虽然功能少一点,却也是很有优势的。1.常数小;2.代码短;3.内存小;
翻了翻学习资料的文件夹,发现关于这两个数据结构的课件还是比较多的,难度分布也非常的广泛...
前两天强行抓着wzx讲这个,感觉在讲的过程中自己也更明白了。
很多课件对于树状数组的原理都避而不谈,自己研究一下就发现其实也没有那么复杂,明白原理之后就不用背代码了,如果考场上忘了也可以现推,还是比较好的。树状数组的常规用法:

1 void add (int x,int a) 2 { 3 while (x<=n) 4 { 5 c[x]+=a; 6 x+=lowbit(x); 7 } 8 }

1 int sum(int x) 2 { 3 int S=0; 4 while(x!=0) 5 { 6 S+=c[x]; 7 x-=lowbit(x); 8 } 9 return S; 10 }
初始化一般是一个一个的加,但是其实还有一种方法可以达到$O(N)$的复杂度,非常优越。

1 void init() 2 { 3 memset(c,0,sizeof(c)); 4 for (R i=1;i<=n;++i) 5 { 6 c[i]+=a[i]; 7 if(i+lowbit(i)<=n) 8 c[i+lowbit(i)]+=c[i]; 9 } 10 }
树状数组有一个特别好的用途就是二维树状数组,二维线段树的代码复杂度比一般线段树要大不少,但是二维树状数组只多两行而已。

1 void add(int v,int x,int y) 2 { 3 for (R i=x;i<=n;i+=lowbit(i)) 4 for (R j=y;j<=m;j+=lowbit(j)) 5 t[i][j]+=v; 6 }

1 int ask(int x,int y) 2 { 3 int ans=0; 4 for (R i=x;i;i-=lowbit(i)) 5 for (R j=y;j;j-=lowbit(j)) 6 ans+=t[i][j]; 7 return ans; 8 }
补充一个内容,二维前缀和:
$X_{1},X_{2},Y_{1},Y_{2}(X_{1}<=X_{2},Y_{1}<=Y_{2}) $区域的和:$S=a[X_2][Y_2]-a[X_1-1][Y_2]-a[X_2][Y_1-1]+a[X_1-1][Y_1-1]$
单点查询区间修改就不用说了,区间修改单点查询用的是差分。一般来说树状数组最大的弊端就是不支持区间修改区间查询。以前我也是这么认为的,后来查资料的时候发现并非如此,可以通过一些巧妙的方法来实现。
首先建立差分数组,把区间和的公式写出来:
$$sum_{i=1}^{n}a_i=c_1+c_1+c_2+c_1+c_2+c_3...$$
$$=sum_{i=1}^nc_i*(n-i+1)$$
当然这样还是不行的,因为乘的数依赖于$n$,所以没法维护,但是我们可以把它反过来;
$$=sum_{i=1}^nc_i*n-sum_{i=1}^nc_i*(i-1)$$
这样就非常棒,维护两个树状数组,一个保存$c$数组,一个保存$c_i*(i-1)$,复杂度还是$NlogN$,但是比线段树的常数要小的多。
现在就有四个操作:1.单点修改,区间查询:单次$logN$
2.区间修改,单点查询:单次$logN$
3.区间修改,区间查询:单次$logN$
4.单点修改,单点查询:单次$logN$ ... 其实还有一种更好的数据结构叫做数组呢...单次$O(1)$,果然是高级数据结构学傻了吧...
那我们就来看看这些代码:
单点修改区间查询:https://www.luogu.org/problemnew/show/P3374

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 5 using namespace std; 6 7 int c[500005]={0},n; 8 9 void add (int x,int v) 10 { 11 for (R i=x;i<=n;i+=(i&(-i))) c[i]+=v; 12 } 13 14 int ask (int x) 15 { 16 int S=0; 17 for (R i=x;i;i-=(i&(-i))) S+=c[i]; 18 return S; 19 } 20 21 int main() 22 { 23 int m,x,a,b,v; 24 scanf("%d%d",&n,&m); 25 for (R i=1;i<=n;i++) 26 { 27 scanf("%d",&v); 28 add(i,v); 29 } 30 for (R i=1;i<=m;i++) 31 { 32 scanf("%d%d%d",&x,&a,&b); 33 if(x==1) 34 add(a,b); 35 if(x==2) 36 printf("%d ",ask(b)-ask(a-1)); 37 } 38 return 0; 39 }
区间修改单点查询:https://www.luogu.org/problemnew/show/P3368

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <algorithm> 6 # include <cmath> 7 # define R register int 8 # define ll long long 9 10 using namespace std; 11 12 int n,m,x,y; 13 ll k,now,last=0; 14 ll t[500005]={0}; 15 ll S=0; 16 int xx; 17 18 void add (int x,ll y) 19 { 20 for (R i=x;i<=n;i+=(i&(-i))) t[i]+=y; 21 } 22 23 ll ask (int x) 24 { 25 ll S=0; 26 for (R i=x;i;i-=(i&(-i))) S+=t[i]; 27 return S; 28 } 29 30 int main() 31 { 32 scanf("%d%d",&n,&m); 33 for (int i=1;i<=n;i++) 34 { 35 scanf("%lld",&now); 36 add(i,now-last); 37 last=now; 38 } 39 for (int i=1;i<=m;i++) 40 { 41 scanf("%d",&xx); 42 if(xx==1) 43 { 44 scanf("%d%d",&x,&y); 45 scanf("%lld",&k); 46 add(x,k); 47 add(y+1,-k); 48 } 49 if (xx==2) 50 { 51 scanf("%d",&x); 52 printf("%lld ",ask(x)); 53 } 54 } 55 return 0; 56 }
区间修改区间查询:https://www.luogu.org/problemnew/show/P3372

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <algorithm> 6 # include <cmath> 7 # define R register int 8 # define ll long long 9 10 using namespace std; 11 12 int m,n,op,x,y,opt; 13 ll a[100004]={0},k,s1,s2; 14 ll c[100004]={0},c1[100004]={0}; 15 16 void add (ll *t,int pos,ll v) 17 { 18 for (R i=pos;i<=n;i+=(i&(-i))) 19 t[i]+=v; 20 } 21 22 ll ask (ll *t,int pos) 23 { 24 ll ans=0; 25 for (R i=pos;i;i-=(i&(-i))) 26 ans+=t[i]; 27 return ans; 28 } 29 30 int main() 31 { 32 scanf("%d%d",&n,&m); 33 for (R i=1;i<=n;++i) 34 { 35 scanf("%lld",&a[i]); 36 add(c,i,a[i]-a[i-1]); 37 add(c1,i,(i-1)*(a[i]-a[i-1])); 38 } 39 for (R i=1;i<=m;++i) 40 { 41 scanf("%d",&opt); 42 if (op==1) 43 { 44 scanf("%d%d%lld",&x,&y,&k); 45 add(c,x,k); 46 add(c,y+1,-k); 47 add(c1,x,k*(x-1)); 48 add(c1,y+1,-k*y); 49 } 50 if (op==2) 51 { 52 scanf("%d%d",&x,&y); 53 s1=(x-1)*ask(c,x-1)-ask(c1,x-1); 54 s2=y*ask(c,y)-ask(c1,y); 55 printf("%lld ",s2-s1); 56 } 57 } 58 return 0; 59 }
树状数组还有一些奇妙的应用,比如求逆序对,用到了一个很奇妙的方法:把值当做下标;还没有写过,下次有空再补;现在已经补在后面了。
计数问题:https://www.luogu.org/problemnew/show/P4054
题意概述:一个矩阵中进行涂色,支持修改,问某个子矩阵中某种颜色出现的次数(在线)。颜色数量小于$100$
既然颜色数量这么少,就可以对于每个颜色单开一个二维树状数组进行统计。

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 5 using namespace std; 6 7 int n,m,c,q,op,x,y,x_1,y_1; 8 int t[101][305][305]; 9 int g[305][305]; 10 11 int read() 12 { 13 int x=0; 14 char c=getchar(); 15 while (!isdigit(c)) 16 c=getchar(); 17 while (isdigit(c)) 18 { 19 x=(x<<3)+(x<<1)+(c^48); 20 c=getchar(); 21 } 22 return x; 23 } 24 25 int lowbit(int x) 26 { 27 return x&(-x); 28 } 29 30 void add(int v,int x,int y,int co) 31 { 32 for (R i=x;i<=n;i+=lowbit(i)) 33 for (R j=y;j<=m;j+=lowbit(j)) 34 t[co][i][j]+=v; 35 } 36 37 int ask(int x,int y,int co) 38 { 39 int ans=0; 40 for (R i=x;i;i-=lowbit(i)) 41 for (R j=y;j;j-=lowbit(j)) 42 ans+=t[co][i][j]; 43 return ans; 44 } 45 46 int main() 47 { 48 n=read(),m=read(); 49 for (R i=1;i<=n;++i) 50 for (R j=1;j<=m;++j) 51 { 52 c=read(); 53 g[i][j]=c; 54 add(1,i,j,c); 55 } 56 q=read(); 57 while (q--) 58 { 59 op=read(); 60 if(op==1) 61 { 62 x=read(),y=read(),c=read(); 63 add(-1,x,y,g[x][y]); 64 g[x][y]=c; 65 add(1,x,y,g[x][y]); 66 } 67 if(op==2) 68 { 69 x=read(),x_1=read(),y=read(),y_1=read(),c=read(); 70 printf("%d ",ask(x_1,y_1,c)-ask(x-1,y_1,c)-ask(x_1,y-1,c)+ask(x-1,y-1,c)); 71 } 72 } 73 return 0; 74 }
上帝造题的七分钟:https://www.luogu.org/problemnew/show/P4514
题意概述:矩形加,矩形求和;
听说这道题卡常,不能写二维线段树,正好我也不会......看起来是个数据结构题,事实上也得化一下式子。
首先这题肯定是要差分的,差分完了再进行修改就好改多了。
如果要在以$(a,b)$,$(c,d)$为两对角的矩形中加$v$,可以用四步完成:
$$(a,b)+v,(a,d+1)-v,(c+1,b)-v,(c+1,d+1)+v$$
一个子矩阵的总和可以用容斥算出来,所以我们现在只看矩阵的左下面积和。($c$数组为差分数组)
$$ sum _{i=1}^xsum_{j=1}^ysum_{k=1}^i sum_{h=1}^jc[k][h] $$
这个式子妙就妙在可以将$O(n^2)$就能完成的运算强行逆优化到$O(n^4)$...
但是这个式子里边依旧有非常多的重复,把它写出来:
$$sum _{i=1}^xsum_{j=1}^yc[i][j]*(x+1-i)*(y+1-j)$$
再进行一些展开:
$$=(x+1)*(y+1)*sum _{i=1}^xsum_{j=1}^yc[i][j]$$
$$ -(y+1)*sum _{i=1}^xsum_{j=1}^yc[i][j]*i$$
$$-(x+1)*sum _{i=1}^xsum_{j=1}^yc[i][j]*j$$
$$+sum _{i=1}^xsum_{j=1}^yc[i][j]*i*j$$
现在开四个树状数组,分别维护$c[i][j]$,$c[i][j]*i$,$c[i][j]*j$,$c[i][j]*i*j$
比较复杂,但也只是个板子题,洛谷评分有点过高了。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 # define lowbit(x) (x&(-x)) 6 7 using namespace std; 8 9 const int maxn=2050; 10 int a,b,c,d,n,m,s1,s2,s3,s4,v; 11 string st; 12 int c1[maxn][maxn],c2[maxn][maxn],c3[maxn][maxn],c4[maxn][maxn]; 13 14 inline int read() 15 { 16 int x=0,f=1; 17 char c=getchar(); 18 while (!isdigit(c)) 19 { 20 if(c=='-') f=-f; 21 c=getchar(); 22 } 23 while (isdigit(c)) 24 { 25 x=(x<<3)+(x<<1)+(c^48); 26 c=getchar(); 27 } 28 return x*f; 29 } 30 31 inline void add(int x,int y,int v) 32 { 33 for (R i=x;i<=n;i+=lowbit(i)) 34 for (R j=y;j<=m;j+=lowbit(j)) 35 { 36 c1[i][j]+=v; 37 c2[i][j]+=v*x; 38 c3[i][j]+=v*y; 39 c4[i][j]+=v*x*y; 40 } 41 } 42 43 inline int ask(int x,int y) 44 { 45 int ans=0; 46 for (R i=x;i;i-=lowbit(i)) 47 for (R j=y;j;j-=lowbit(j)) 48 { 49 ans+=(x+1)*(y+1)*c1[i][j]; 50 ans-=(y+1)*c2[i][j]; 51 ans-=(x+1)*c3[i][j]; 52 ans+=c4[i][j]; 53 } 54 return ans; 55 } 56 57 int main() 58 { 59 scanf("X %d %d",&n,&m); 60 while (cin>>st) 61 { 62 if(st[0]=='L') a=read(),b=read(),c=read(),d=read(),v=read(); 63 else a=read(),b=read(),c=read(),d=read(); 64 if(st[0]=='L') 65 { 66 add(a,b,v); 67 add(a,d+1,-v); 68 add(c+1,b,-v); 69 add(c+1,d+1,v); 70 } 71 else 72 printf("%d ",ask(c,d)-ask(c,b-1)-ask(a-1,d)+ask(a-1,b-1)); 73 } 74 return 0; 75 }
平衡的照片:https://www.luogu.org/problemnew/show/P3608
题意概述:给定一个数列,l[i]表示i的左边比a[i]大的数,r[i]表示右边,如果l[i],r[i]中的一个是另一个的两倍还多,这个数就是一个不平衡的数,问数列中有几个不平衡的数。
树状数组求逆序对,正反各一次。别忘了离散化。

1 // luogu-judger-enable-o2 2 # include <cstdio> 3 # include <iostream> 4 # include <cstring> 5 # include <algorithm> 6 # define R register int 7 # define lowbit(i) (i&(-i)) 8 9 using namespace std; 10 11 const int maxn=100009; 12 int ans=0,n,num[maxn],h[maxn]; 13 int l[maxn],r[maxn],c[maxn]; 14 struct nod 15 { 16 int v,rk; 17 }a[maxn]; 18 19 bool cmp(nod a,nod b) 20 { 21 return a.v<b.v; 22 } 23 24 void add(int x) 25 { 26 for (R i=x;i<=n;i+=lowbit(i)) 27 c[i]++; 28 } 29 30 int ask(int x) 31 { 32 int ans=0; 33 for (R i=x;i;i-=lowbit(i)) 34 ans+=c[i]; 35 return ans; 36 } 37 38 int main() 39 { 40 scanf("%d",&n); 41 for (R i=1;i<=n;++i) 42 scanf("%lld",&a[i].v),a[i].rk=i,h[i]=a[i].v; 43 sort(a+1,a+1+n,cmp); 44 for (R i=1;i<=n;++i) 45 num[ a[i].rk ]=i; 46 for (R i=1;i<=n;++i) 47 { 48 add(num[i]); 49 l[i]=ask(n)-ask(num[i]); 50 } 51 memset(c,0,sizeof(c)); 52 for (R i=n;i>=1;--i) 53 { 54 add(num[i]); 55 r[i]=ask(n)-ask(num[i]); 56 } 57 for (R i=1;i<=n;++i) 58 if(max(l[i],r[i])>(min(l[i],r[i])*2)) ans++; 59 printf("%d",ans); 60 return 0; 61 }
三元上升子序列:https://www.luogu.org/problemnew/show/P1637
题意概述:给定一个数列,求$i<j<k$,且$a[i]<a[j]<a[k]$的数对数量。
求出以每个数为开头的正序对数量以及以他为结尾的逆序对数量,相乘。“离散化时有没有去重...”

1 # include <cstdio> 2 # include <iostream> 3 # include <algorithm> 4 # define R register int 5 # define lowbit(i) (i&(-i)) 6 7 int n,h[30009]; 8 int b[30009],c[30009],t[30009],c_1[30009],num[30009]; 9 long long ans=0; 10 struct nod 11 { 12 int v,rk; 13 }a[30009]; 14 15 bool cmp (nod a,nod b) 16 { 17 return a.v<b.v; 18 } 19 20 void add (int *t,int x) 21 { 22 for (R i=x;i<=n;i+=lowbit(i)) 23 t[i]++; 24 } 25 26 int ask (int *t,int x) 27 { 28 int ans=0; 29 for (R i=x;i;i-=lowbit(i)) 30 ans+=t[i]; 31 return ans; 32 } 33 34 int main() 35 { 36 scanf("%d",&n); 37 for (R i=1;i<=n;++i) 38 { 39 scanf("%d",&a[i].v); 40 a[i].rk=i; 41 } 42 std::sort(a+1,a+1+n,cmp); 43 int val=1; 44 a[0].v=a[1].v; 45 for (R i=1;i<=n;++i) 46 { 47 if(a[i].v!=a[i-1].v) val++; 48 num[ a[i].rk ]=val; 49 } 50 for (R i=1;i<=n;++i) 51 { 52 add(c,num[i]); 53 b[i]=ask(c,num[i]-1); 54 } 55 for (R i=n;i>=1;--i) 56 { 57 add(c_1,num[i]); 58 ans+=(long long)b[i]*(ask(c_1,n)-ask(c_1,num[i])); 59 } 60 printf("%lld",ans); 61 return 0; 62 }
跑步:无
一道很有趣的题目。
首先一个显然的事实是修改一个数后,随之修改的必然是它右下角的矩形中的一些点。但是如果只是这样暴力就成 $n^3$ 的了。
另一个比较显然的性质是:如果一个数的正上方和左方都被修改了,那么它肯定是要修改的。又因为每一行的修改区间是连续的,所以每一行的左端点是单调的,右端点也是单调的,画出来就是这样的形状:
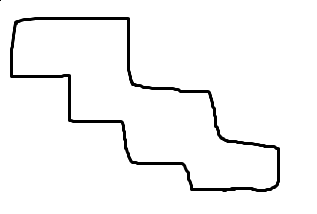
所以依据这个性质,就可以 $O(N)$ 的找到每一行的左右端点,再用树状数组修改即可。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <cmath> 5 # define R register int 6 # define ll long long 7 8 using namespace std; 9 10 const int maxn=2003; 11 int n,x,y,maxx; 12 int a[maxn][maxn]; 13 ll ans,dp[maxn][maxn],t[maxn][maxn],tl,v; 14 char c[5]; 15 16 inline int read() 17 { 18 R x=0; 19 char c=getchar(); 20 while (!isdigit(c)) c=getchar(); 21 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 22 return x; 23 } 24 25 void add (int x,int y,ll v) { for (R i=y;i<=n;i+=(i&(-i))) t[x][i]+=v; } 26 ll ask (int x,int y) 27 { 28 ll ans=0; 29 for (R i=y;i;i-=(i&(-i))) ans+=t[x][i]; 30 return ans; 31 } 32 33 int main() 34 { 35 scanf("%d",&n); 36 for (R i=1;i<=n;++i) 37 for (R j=1;j<=n;++j) 38 a[i][j]=read(); 39 for (R i=1;i<=n;++i) 40 for (R j=1;j<=n;++j) 41 { 42 dp[i][j]=max(dp[i-1][j],dp[i][j-1])+a[i][j],ans+=dp[i][j]; 43 add(i,j,dp[i][j]-dp[i][j-1]); 44 } 45 printf("%lld ",ans); 46 for (R T=1;T<=n;++T) 47 { 48 scanf("%s",c); 49 x=read(),y=read(); 50 int l=y,r=y+1; 51 if(c[0]=='U') v=1,a[x][y]++; 52 else a[x][y]--,v=-1; 53 for (R i=y+1;i<=n;++i) 54 { 55 tl=ask(x,i); 56 if(max(ask(x-1,i),ask(x,i-1)+v)+a[x][i]!=tl) r++; 57 else break; 58 } 59 add(x,l,v); if(r<=n) add(x,r,-v); 60 ans+=(r-l)*v; 61 for (R i=x+1;i<=n;++i) 62 { 63 while(l<=n) 64 { 65 tl=ask(i,l); 66 if(max(ask(i-1,l),ask(i,l-1))+a[i][l]!=tl) break; 67 else l++; 68 } 69 if(l>n) break; 70 while(r<=n) 71 { 72 tl=ask(i,r); 73 if(max(ask(i-1,r),ask(i,r-1)+((l<=r-1)?v:0))+a[i][r]!=tl) r++; 74 else break; 75 } 76 add(i,l,v); if(r<=n) add(i,r,-v); 77 ans+=(r-l)*v; 78 } 79 maxx=0; 80 printf("%lld ",ans); 81 } 82 return 0; 83 }
贪婪大陆:https://www.luogu.org/problemnew/show/P2184
[如果你看到这行字,请联系我更新].
---shzr
