题目:
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
分析:
从外向内顺时针打印每个数字,先不考虑特殊情况,实际上每打印一次外圈至多需要四步,从起始点开始从左向右打印,再从上到下,从右向左,最后再从下到上打印。而且每打印完一圈下次打印的起始坐标都是上次打印起点的右下的元素,考虑一个6*6的矩阵,先从[0,0]的位置开始打印一圈,下次开始则是从[1,1]打印,然后再从[2,2],也就是说如果知道了起始点的坐标,和要打印的矩形范围,便可顺时针打印。
不过根据矩形的大小,有时是不需要4步来打印的。例如:
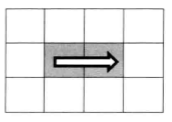
这种一行n列的矩阵,只需要从左到右打印一次即可,而且不难发现无论什么情况,都需要从左到右打印一次。
当需要第二步打印的情况如下:
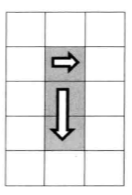
也就是行数要大于1,才需要第二步的打印。
需要第三步从右到左的打印情况如下:
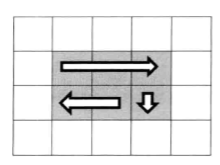
不难看出,需要矩形的列数和行数均大于1,才会需要第三步的打印。
而第四步的打印举例如下:
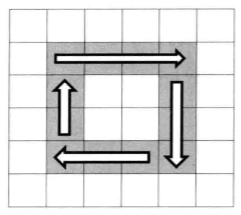
列数大于1,而行数要求大于2.才会需要第四步的打印。
在每次打印外圈数字时,都要判断是否需要2,3,4步的打印。最后还要写好循环的退出条件,也就是没有矩形再需要打印了。
程序:
C++
class Solution { public: vector<int> printMatrix(vector<vector<int> > matrix) { if(matrix.empty()) return res; int m = matrix.size()-1; int n = matrix[0].size()-1; int i = 0; while((n-i) >= 0 && (m-i) >= 0){ readHelper(matrix, i, i, m--, n--); i++; } return res; } void readHelper(vector<vector<int>> &v, int x, int y, int m, int n){ //left to right int i = x; int j = y; for(; j <= n; ++j) res.push_back(v[i][j]); //up to down if(m-x > 0){ for(i = x+1, j = n; i <= m; ++i) res.push_back(v[i][j]); } //right to left if(m-x > 0 && n - y > 0){ for(j = n-1, i = m; j >= y; --j) res.push_back(v[i][j]); } //down to up if(m-x > 1 && n - y > 0){ for(i = m-1, j = y; i > x; --i) res.push_back(v[i][j]); } } private: vector<int> res; };
Java
import java.util.ArrayList; public class Solution { public ArrayList<Integer> printMatrix(int [][] matrix) { res = new ArrayList<>(); if( matrix.length == 0) return res; int m = matrix.length-1; int n = matrix[0].length-1; int index = 0; while(m-index >= 0 && n-index >= 0){ helper(matrix, index, index, m--, n--); index++; } return res; } public void helper(int [][] matrix, int x, int y, int endX, int endY){ for(int j = y; j <= endY; ++j) res.add(matrix[x][j]); if((endX - x) > 0){ for(int i = x+1; i <= endX; ++i) res.add(matrix[i][endY]); } if((endX - x) > 0 && (endY - y) > 0){ for(int j = endY-1; j >= y; --j) res.add(matrix[endX][j]); } if((endX - x) > 1 && (endY - y) > 0){ for(int i = endX-1; i > x; --i) res.add(matrix[i][y]); } } private ArrayList<Integer> res; }