4.机器调度问题
m台机器,n个任务,每个任务时间可能不一致,求如何分配,在最短的时间完成任务?
def machine(time_list,m): time_list.sort(reverse=True) if len(time_list)<=m: return time_list[0] else: temp = time_list[0:m] for i in time_list[m:]: min_index = temp.index(min(temp)) temp[min_index]+=i return max(temp) re = machine([33,44,55,23],3) print(re)
简单解析:先排序,n个任务按时间从大到小降序,m个机器按时间长短各排好一个任务,未排上的第一个任务时间是剩下任务时间中最长的,将归属于最后一个机器,因为归属于其他机器累计时间会更长,未排上的第二个任务同理给m个机器中时间最少的那个,此时时间最少的不一定是最后的那个机器,依此类推。
5.背包问题
weight = [5, 3, 4, 2] value = [6, 4, 5, 3] max_weight = 8 def bag(weight, value, max_weight): weight.insert(0, 0) value.insert(0, 0) thing_num = len(weight) # 建立一个thing_num * (max_weight+1)的二维矩阵 5*9 dp = [] for i in range(thing_num): dp.append([0]*(max_weight+1)) for i in range(1,thing_num): for j in range(1,max_weight+1): dp[i][j] = dp[i-1][j] if j>=weight[i]: dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]) return dp[-1][-1] re = bag(weight, value, max_weight) print(re)
目标:以有限的背包容量装最大化价值物品,本例背包最大容量为8,物品有四个,对应容量和价值如上所示。
简单解析:二维矩阵动态规划分析,纵轴方向是前 i 个物品选择放入背包(以下称为状态),横轴方向是背包容量从0到8(以下称为容量),个人理解:二维表是从左至右,从上至下逐一填写记录,填写的值是包中物品的总价值,value值按右下方向是逐渐增大的,基本理论:1.如果此时物品放不下,则包中价值为上一状态同等容量的价值;2.如果此时物品能装入包中,但不能判定装此物品价值一定高于上个状态(未装此物品)的价值,所以包价值=max(上一状态同等容量的价值,上一状态减去该物品容量的价值+该物品的价值),此处不易理解,放图说明:
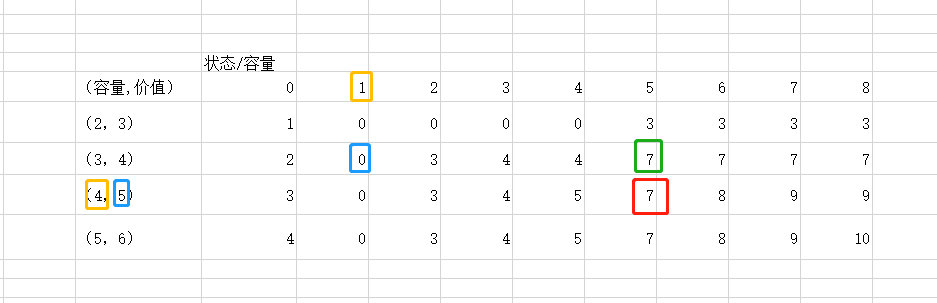
红框值指的是状态为3容量为5的价值,也就是容量为2,3,4的三种物品随机组合放入容量为5的背包中的最大价值。它怎么推出来的呢?
首先,判断状态3新加的物品容量(4)是否大于背包容量(5),所以新物品是可以装到包中的;
满足上述基本理论2,所以接下来算max括号里的东西就好了:
上一状态同等容量的价值 = 绿框的值 = 7,
上一状态减去该物品容量的价值+该物品的价值 = 蓝框的值的总和 = 0+5
(脑子直观感受就是,容量为5,装上4,价值为5,但容量只剩下1,再也装不了了,总价值为5;仍然只装2和3的话,正好装上,价值为3+4)
出现了装上新物体反而价值低的情况,所以选择上一状态的价值,保持一直递增的记录,最终得出容量为8,状态为4的最终价值。