主要解决在样本的分布没有足够的先验,也就是说我们不仅不知道分布的参数,连是什么类型的分布都不知道,这种情况下显然不能用参数估计的方法。这里从简单直观的方法——直方图法入手,引出KNN和Parzen窗两种方法。
直方图密度估计:出发点是分布函数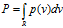 ,假设在某一个很小很小的超立方体V中是均匀分布,那么有
,假设在某一个很小很小的超立方体V中是均匀分布,那么有 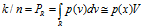
我们就可以得到关于概率密度函数p(x)的估计了 。
。
但是要有几个苛刻的条件
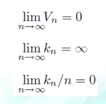
通俗的说就是,在样本数量n不断增加趋于无穷大时,要让小舱体积v尽可能小,同时小舱内有充分多的样本k,但是每个小舱内的样本数又必须是总体样本数中很小的一部分。所以小舱的选择会对估计的效果产生直接影响,那么下面就给出两种选择小舱方法。
KNN:
基本做法:固定局部区域K,体积V进行变化。
需要人为调定一个参数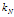 ,代表的是在总样本数量是N 的情况下我们要使得每个框中落入的样本个数。
,代表的是在总样本数量是N 的情况下我们要使得每个框中落入的样本个数。
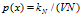 一般选取
一般选取 .
.
Parzen窗:
基本做法:固定局部区域体积V,k变化。
要给出一个窗函数:这里以方窗函数为例(通常也可以有高斯窗,可能更有普遍意义)

那么以点x为中心,体积为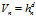 的局部区域内的样本个数为
的局部区域内的样本个数为
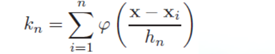
这个式子就表示了与x的距离为 的样本点会被冠以权重1,然后计入
的样本点会被冠以权重1,然后计入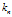 中,距离超过
中,距离超过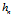 就冠以权重0计入。
就冠以权重0计入。
由 得到
得到
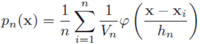
其中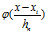 被称为是核函数,通常会有高斯核,方窗核,超球核,指数分布核(抑制噪声的效果更好一点。从分布密度的形状可以看出这一点)。他们要满足概率密度的要求(非负,积分为1)。
被称为是核函数,通常会有高斯核,方窗核,超球核,指数分布核(抑制噪声的效果更好一点。从分布密度的形状可以看出这一点)。他们要满足概率密度的要求(非负,积分为1)。
h被称为带宽,带宽越大越平滑,带宽越小越容易接近样本值也就越容易产生过拟合。
当样本量不足时要适当加大带宽以减少噪声。