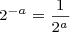2的幂可以合并，遵守幂运算规则，产生一个新的2的幂。在这些规则下，你可以进行2的幂的乘法，除法，或幂运行，得到另外一个2的幂。你可以组合这些规则来创建一个复杂的表达式，该表达式返回一个2的幂。例如，
.
幂的运算法则适用于任意进制的基数；二进制也没有不同。但因为我们对2的幂感兴趣，我们将依据2的幂来描述它们。只要我们如此解释过这些规则，你就会明白上面例子背后的数学原理。
基本的2的幂运算规则
下面是基本的2的幂的运算规则，如果你知道2的幂是何物那这些规则你应该很熟悉：
2的幂组合运算规则
下面是2的幂的乘，除，幂运算的组合运算规则：
2的幂的求积规则： 
这个规则告诉我们2的幂乘以2的幂结果还是2的幂。只是结果中的指数是乘法中两个2的幂的指数的和。
例如：
2的幂的求商规则： 
这个规则告诉我们一个2的幂除以另一个2的幂结果还是2的幂。只是，结果中2的幂的指数是被除数指数与除数指数的差。
例如:
2的幂的求幂规则: 
这条规则告诉我们2的幂的幂运算得到的还是一个2的幂。只是，结果中2的幂的指数是给出的两个指数的乘积。
例如:
2的幂的复合运算规则
除基本的幂运算规则还有两条附加规则：乘法的幂运算和除法的幂运算。对2的幂来说，这些规则变得不那么重要，因为它们能分解成上面的小规则。尽管如此，它们是合法的，在需要的时候可以化简运算。
2的幂乘积的幂运算规则： 
此规则只是2的幂的求积规则和2的幂的求幂规则的合并。
例如:
2的幂商的幂运算规则： 
此规则只是2的幂的求商运算规则和2的幂的求幂规则的合并。
例如:
2的幂的任意运算式
你可以利用上面的规则来简化复杂运算式为
的形式。回到文章开头的例子：
有多种化简方式。下面是不用任何复合规则的方式：
下面使用了复合规则:
下面是不适用复合规则的另一种更长的方式：
2的幂的转换
如果表达式中使用了2的幂的数值形式--例如，用64代替
— transform them to the form . 仍遵守上述规则。例如：
.
一个可视化例子
你将在下表看到幂运算规则的应用：
一个 4" x 4" x 4" 立方体.
有三种等价的方式求立方体的体积：
- 长 x 宽 x 高: 4 x 4 x 4 = 64 立方英寸
- 长 x 宽 x 高:
x x 
64 立方英寸 - 长的立方:
64 立方英寸
有三种等价的方式求每一面的面积：
- 长 x 宽: 4 x 4 = 16 平方英寸
- 长 x 宽:
16 平方英寸 - 体积 / 高:
16 平方英寸
