HMM学习 viterbi算法2

维特比算法

维特比算法的形式化定义

维特比算法可以形式化的概括为：
对于每一个i，i = 1，… ，n，令：Xi=(Xi1,Xi2,Xi3,Xi4...,XiT)$X_i=(X_{i1},X_{i2},X_{i3},X_{i4}...,X_{iT})$.
这一步是通过隐藏状态的初始概率和相应的观察概率之积计算了t=1时刻的局部概率。
对于t=2，…，T和i=1，…，n,令：

δt(i)=maxj(δt−1(j)ajibikt)$${\delta }_t(i)=ma{x}_j({\delta }_{t-1}(j)a_{ji}{b}_{i{k}_t})$$

ϕt(i)=argmaxj(δt−1(j)aji)$${\varphi }_t(i)=argma{x}_j({\delta }_{t-1}(j)a_{ji})$$

这样就确定了到达下一个状态的最可能路径，并对如何到达下一个状态做了记录。具体来说首先通过考察所有的转移概率与上一步获得的最大的局部概率之积，然后记录下其中最大的一个，同时也包含了上一步触发此概率的状态。
令：it=argmax(δT(i))$i_t=argmax({\delta }_T(i))$, 这就确定了系统完成时（t=T）最可能的隐藏状态。
对于t=T-1，…，1，令it=ϕt+1(it+1)$i_t={\varphi }_{t+1}(i_{t+1})$，这样就可以按最可能的状态路径在整个网格回溯。回溯完成时，对于观察序列来说，序列i1,i2,i3...iT$i_1,i_2,i_3...i_T$就是生成此观察序列的最可能的隐藏状态序列。

计算单独的δ$\delta$和ϕ$\varphi$

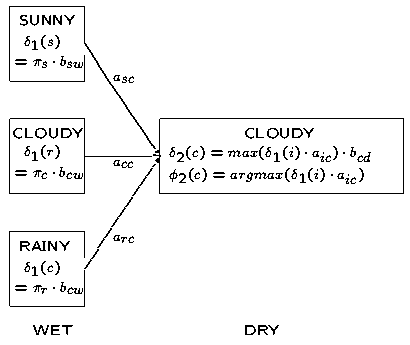
下面这幅图表显示了δ$\delta$和ϕ$\varphi$的计算细节, 在维特比算法中我们选择的是到达当前状态的最可能路径，而不是总的概率。我们在维特比算法中维护了一个“反向指针”记录了到达当前状态的最佳路径，即在计算ϕ$\varphi$时通过argmax$argmax$运算符获得。

总结

对于一个特定的隐马尔科夫模型，维特比算法被用来寻找生成一个观察序列的最可能的隐藏状态序列。我们利用概率的时间不变性，通过避免计算网格中每一条路径的概率来降低问题的复杂度。维特比算法对于每一个状态(t>1)都保存了一个反向指针(ϕ$\varphi$)，并在每一个状态中存储了一个局部概率(δ$\delta$)。
局部概率δ$\delta$是由反向指针指示的路径到达某个状态的概率。
　　当t=T时，维特比算法所到达的这些终止状态的局部概率δ$\delta$是按照最优（最可能）的路径到达该状态的概率。因此，选择其中最大的一个，并回溯找出所隐藏的状态路径，就是这个问题的最好答案。
　　关于维特比算法，需要着重强调的一点是它不是简单的对于某个给定的时间点选择最可能的隐藏状态，而是基于全局序列做决策——因此，如果在观察序列中有一个“非寻常”的事件发生，对于维特比算法的结果也影响不大。
　　这在语音处理中是特别有价值的，譬如当某个单词发音的一个中间音素出现失真或丢失的情况时，该单词也可以被识别出来。

维特比算法程序示例　

程序来自 UMDHMM C语言版本的HMM工具包中的维特比算法程序。维特比算法程序示例如下（在viterbi.c中):

void Viterbi(HMM *phmm, int T, int *O, double **delta, int **psi,int *q, double *pprob)
{
　　int i, j; /* state indices */
　　int t; /* time index */

　　int maxvalind;
　　double maxval, val;

　　/* 1. Initialization */

　　for (i = 1; i <= phmm->N; i++)
　　{
　　　　delta[1][i] = phmm->pi[i] * (phmm->B[i][O[1]]);
　　　　psi[1][i] = 0;
　　}

　　/* 2. Recursion */
　　for (t = 2; t <= T; t++) 　　{ 　　　　for (j = 1; j <= phmm->N; j++)
　　　　{
　　　　　　maxval = 0.0;
　　　　　　maxvalind = 1;
　　　　　　for (i = 1; i <= phmm->N; i++)
　　　　　　{
　　　　　　　　val = delta[t-1][i]*(phmm->A[i][j]);
　　　　　　　　if (val > maxval)
　　　　　　　　{
　　　　　　　　　　maxval = val;
　　　　　　　　　　maxvalind = i;
　　　　　　　　}
　　　　　　}

　　　　　　delta[t][j] = maxval*(phmm->B[j][O[t]]);
　　　　　　psi[t][j] = maxvalind;

　　　　}
　　}

　　/* 3. Termination */

　　*pprob = 0.0;
　　q[T] = 1;
　　for (i = 1; i <= phmm->N; i++)
　　{
　　　　if (delta[T][i] > *pprob)
　　　　{
　　　　　　*pprob = delta[T][i];
　　　　　　q[T] = i;
　　　　}
　　}

　　/* 4. Path (state sequence) backtracking */

　　for (t = T - 1; t >= 1; t--)
　　　　q[t] = psi[t+1][q[t+1]];

}

　在UMDHMM包中所生成的4个可执行程序中，testvit是用来测试维特比算法的， 对于给定的观察符号序列及HMM，利用Viterbi算法生成最可能的隐藏状态序列。这里我们利用UMDHMM包中test.hmm和test.seq来测试维特比算法，关于这两个文件，具体如下：
test.hmm

       M= 2
　　　　N= 3
　　　　A:
　　　　0.333 0.333 0.333
　　　　0.333 0.333 0.333
　　　　0.333 0.333 0.333
　　　　B:
　　　　0.5 0.5
　　　　0.75 0.25
　　　　0.25 0.75
　　　　pi:
　　　　0.333 0.333 0.333

test.seq

　　　　T= 10
　　　　1 1 1 1 2 1 2 2 2 2

对于维特比算法的测试程序testvit来说，运行：testvit test.hmm test.seq
结果如下：

　 Viterbi using direct probabilities
　　Viterbi MLE log prob = -1.387295E+01
　　Optimal state sequence:
　　T= 10
　　2 2 2 2 3 2 3 3 3 3
　　//------------------------------------
　　Viterbi using log probabilities
　　Viterbi MLE log prob = -1.387295E+01
　　Optimal state sequence:
　　T= 10
　　2 2 2 2 3 2 3 3 3 3
　　//------------------------------------
　　The two log probabilites and optimal state sequences
　　should identical (within numerical precision). 

序列“2 2 2 2 3 2 3 3 3 3”就是最终所找到的隐藏状态序列。好了，维特比算法这一章就到此为止了。

---

转自：“我爱自然语言处理”：www.52nlp.cn
链接：http://www.52nlp.cn/hmm-learn-best-practices-six-viterbi-algorithm-5
译自：http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html