-----------------siwuxie095
图的遍历
图的遍历 分为:深度优先搜索 和 广度优先搜索
不同的方式在遍历时,遍历路径是不一样的
深度优先搜索
对如下图进行深度优先搜索:
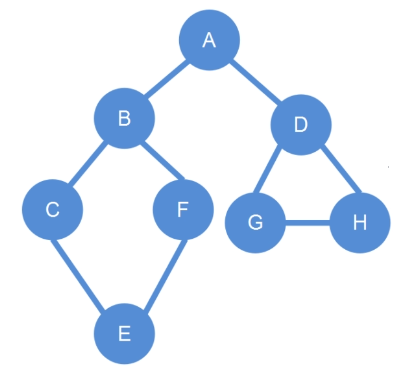
需要先选定一个点,假设选定的点为 A
先从 A 的一支开始搜索,搜索到 B,接着:
从 B 搜索到 C,从 C 搜索到 E,从 E 搜索到 F,直到
从 F 再搜索时已经形成了一个环为止
再从 A 的另一支开始搜索,搜索到 D,接着:
从 D 搜索到 G,从 G 搜索到 H,直到从 H 再搜索时
已经形成了一个环为止
通过上面的搜索过程,不难发现,这与二叉树的前序遍历的
根 - 左 - 右 模式 非常相似
其实,对于图的深度优先搜索来说, 就是前序遍历:
先搜索根,然后再搜索与根连接的每一个节点,而且需要深入
到这个节点的最终端
最后:
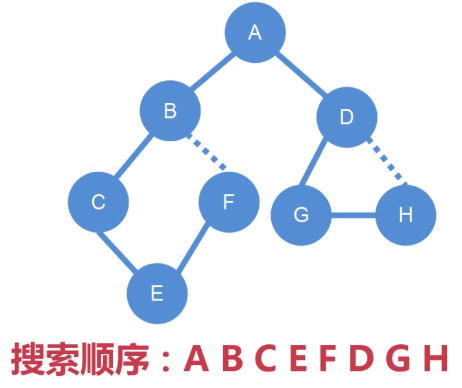
深度优先搜索的顺序:A B C E F D G H
其中:B 到 F 的边,和 D 到 H 的边,需要舍弃掉,
因为它们已经使得当前的这棵树形成了一个环
广度优先搜索
广度优先搜索 其实比 深度优先搜索 更容易理解
对如下图进行广度优先搜索:
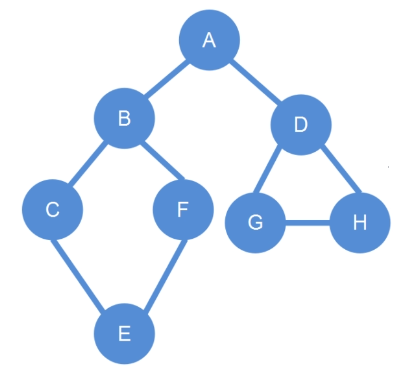
如果把这张图分成层,广度优先搜索其实就是一层一层的去搜索,
它的搜索顺序就是先搜索 A,再搜索 B、D,然后搜索 C、F、G、
H,最后搜索 E
最后:
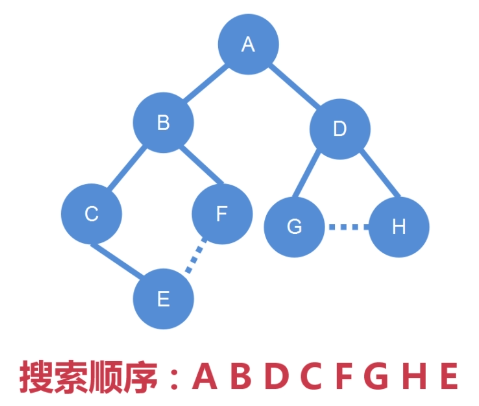
广度优先搜索的顺序:A B D C F G H E
其中:E 到 F 的边,和 G 到 H 的边,需要舍弃掉,
因为它们已经使得当前的这棵树形成了一个环
最小生成树
通过对 深度优先搜索 和 广度优先搜索 的了解,不难发现,
采用不同的搜索方式,形成的生成树是不一样的
但是这样的遍历,其实还是相对比较简单的,它并没有涉及
到权值的问题。在一张图中,顶点和顶点之间的边如果是有
权值的,它的问题将会更加复杂
这样,就涉及到 最小生成树 的问题
看如下实例:
有这样六个城市,分别叫 A、B、C、D、E、F,需要在六个城市
之间修路(可以看成是六个顶点)
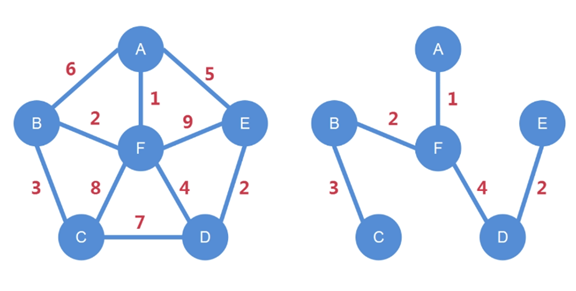
其实每两个城市之间都可以修路,但是修路的成本可能不一样,中间也许隔着山
如:从 A 市修向 B 市,如果中间隔着山,成本就会很高,假设权值为 6
那就不如先从 A 市修到 F 市,再从 F 市修到 B 市,这样,总权值才为 3
可见:如果有了权值之后,想把所有顶点全部连接起来,且使得最后连接
起来的结果最为经济,这样,就是一颗最小生成树
希望达到的结果是这样:
从 A 开始:A 修到 F,F 修到 B,B 修到 C,F 修到 D,D 修到 E
不难发现,选择的全是值比较小的边,而加起来的总成本也最小
但是,有了左图,通过它去求一棵最小生成树,从而达到右图的
效果,却是需要一套算法的
这样的算法,共有两种:

一种叫做 普里姆(Prim)算法,一种叫做 克鲁斯卡尔(Kruskal)算法
普里姆(Prim)算法
普里姆(Prim)算法的基本思想:
1)首先要有一个点集合,是指纳入到最小生成树中的点集合
2)其次要有一个边集合,是指纳入到最小生成树中的边集合
3)最后要有一个待选边集合,是指被选定点可以到达的所有边的集合
第一步:
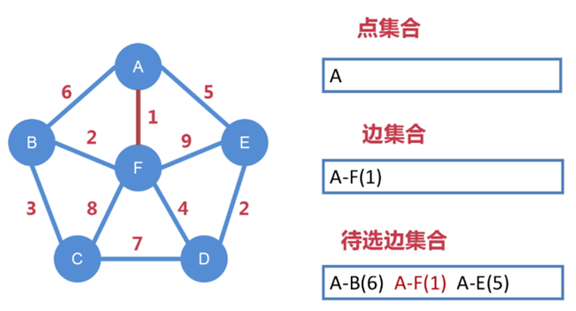
假设从 A 点开始,则 A 就是选定的第一个点,把 A 纳入到点集合中
从 A 向外延伸出去一共有三条边,分别是 A-B、A-F、A-E,把这三
条边纳入到待选边集合中
从待选边集合中找出权值最小的边,即 A-F,把 A-F 纳入到边集合中
这样,第一个点 和 第一条边 就确定下来了
第二步:
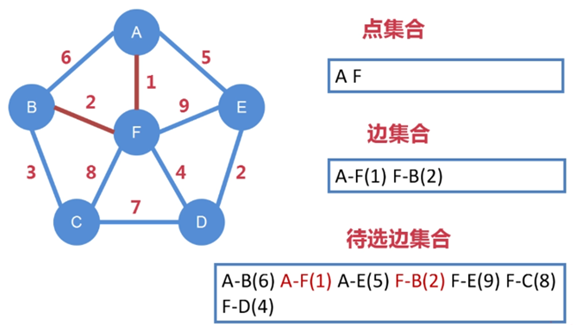
边 A-F 连接了下一个点 F,把 F 纳入到点集合中
把从 A、F 向外延伸出的所有边都纳入到待选边集合中
待选边集合进一步扩充,变成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D
「注意:同一条边,不需要重复写,如:A-F 和 F-A」
其中 A-F 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 F-B,把 F-B 纳入到边集合中
第三步:
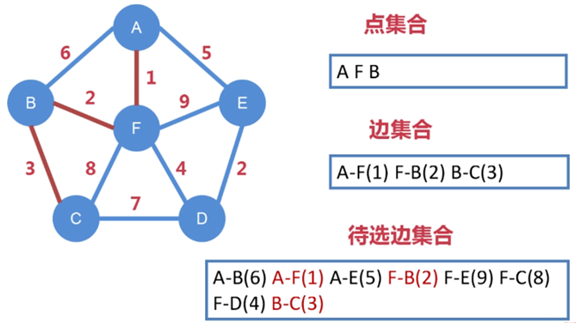
边 F-B 连接了下一个点 B,把 B 纳入到点集合中
把从 A、F、B 向外延伸出的所有边都纳入到待选边集合中
待选边集合进一步扩充,变成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D、B-C
其中 A-F、F-B 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 B-C,把 B-C 纳入到边集合中
第四步:
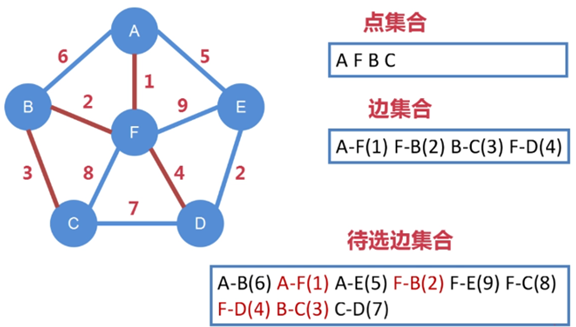
边 B-C 连接了下一个点 C,把 C 纳入到点集合中
把从 A、F、B、C 向外延伸出的所有边都纳入到待选边集合中
待选边集合进一步扩充,变成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D、B-C、C-D
其中 A-F、F-B、B-C 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 F-D,把 F-D 纳入到边集合中
第五步:
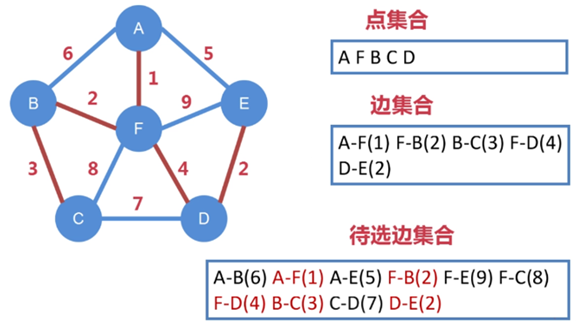
边 F-D 连接了下一个点 D,把 D 纳入到点集合中
把从 A、F、B、C、D 向外延伸出的所有边都纳入到待选边集合中
待选边集合进一步扩充,变成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D、B-C、C-D、D-E
其中 A-F、F-B、B-C、F-D 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 D-E,把 D-E 纳入到边集合中
第六步:
边 D-E 连接了下一个点 E,把 E 纳入到点集合中
此时,点集合中有 A、F、B、C、D、E,即 全部六个点都被连接
了起来,形成了一棵最小生成树
克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔(Kruskal)算法的基本思想:
1)首先要有一个待选边集合,是指一张图中所涉及的所有边的集合
1)其次要有一个已选边集合,是指纳入到最小生成树中的边集合
2)最后要有一个已涉及点集合,是指纳入到最小生成树中的点集合
第一步:
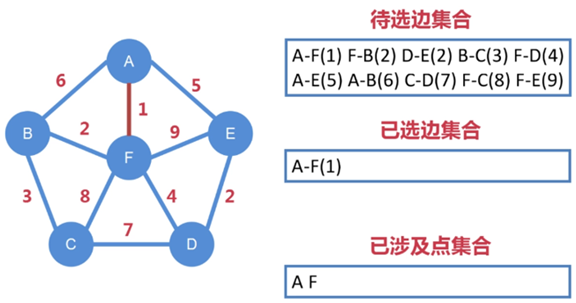
首先把这张图中所涉及的所有边都纳入到待选边集合中
从待选边集合中找出权值最小的边,即 A-F,把 A-F 纳入到已选边集合中
选定边的同时,也选定了点,把 A、F 纳入到第一个已涉及点集合中
第二步:
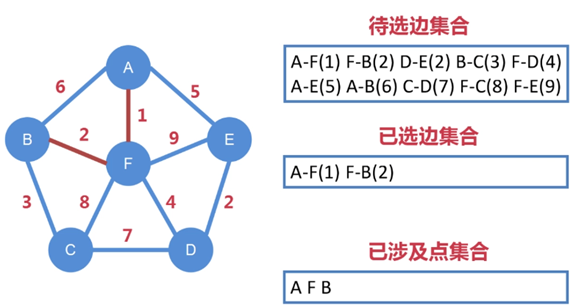
待选边集合中 A-F 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 F-B,把 F-B 纳入到已选边集合中
选定边的同时,也选定了点,把 B 纳入到第一个已涉及点集合中
其实 D-E 的权值也为 2,F-B 和 D-E 二者任选其一即可,这里先选 F-B,
F-B 选出来之后、纳入到已选边集合之前,要判断一下:
当前的 F-B 有没有与以前的 A-F 形成闭环,如果形成了闭环,就需要将
这条边抛弃掉
显然,这里没有形成闭环,于是 F-B 这条边就被纳入到已选边集合中
即 每次从待选边集合中选边时,都要做如下操作:
1)当最小权值的边有多条时,任选其一
2)如果当前选定的边与已选边集合中的边形成了闭环,
就将这条边抛弃掉,重新选择
第三步:
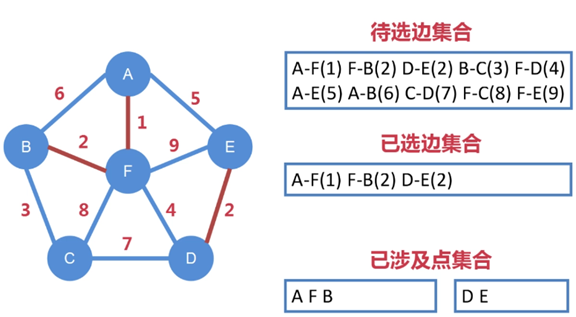
待选边集合中 A-F、F-B 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 D-E,把 D-E 纳入到已选边集合中
注意:默认在 D-E 纳入到已选边集合之前,就已经判断没有形成闭环
选定边的同时,也选定了点,把 D、E 纳入到第二个已涉及点集合中
因为通过已选定边集合无法让 A、F、B 和 D、E 相连,所以要纳入到
两个不同的已涉及点集合中
第四步:
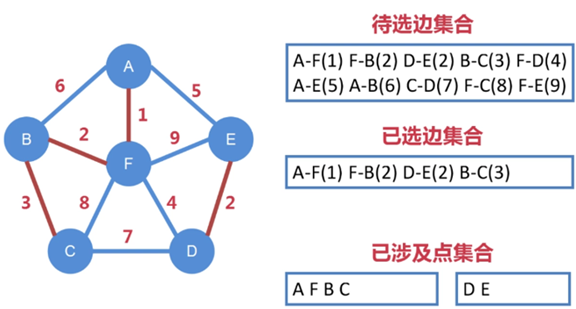
待选边集合中 A-F、F-B、D-E 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 B-C,把 B-C 纳入到已选边集合中
注意:默认在 B-C 纳入到已选边集合之前,就已经判断没有形成闭环
选定边的同时,也选定了点,把 C 纳入到第一个已涉及点集合中
因为通过已选定边集合无法让 A、F、B、C 和 D、E 相连,所以要纳入到
两个不同的已涉及点集合中
第五步:

待选边集合中 A-F、F-B、D-E、B-C 已被选走,不能再被选
从剩下待选边集合中找出权值最小的边,即 F-D,把 F-D 纳入到已选边集合中
注意:默认在 F-D 纳入到已选边集合之前,就已经判断没有形成闭环
已选定边集合中的 F-D 使得两个不同的已涉及点集合中的 F 和 D 关联了起来,
即 两个不同的已涉及点集合有了联系,融合成为一个已涉及点集合
此时,已涉及点集合中有 A、F、B、D、E、C,即 全部六个点都被连接
了起来,形成了一棵最小生成树
【made by siwuxie095】