[OI学习笔记]拓补排序

例题

　　传送门

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n1,2,…,n的 nn个火车站。每个火车站都有一个级别，最低为 11 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 xx，则始发站、终点站之间所有级别大于等于火车站xx 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点） 

例如，下表是55趟车次的运行情况。其中，前44 趟车次均满足要求，而第 55 趟车次由于停靠了 33 号火车站（22 级）却未停靠途经的 66 号火车站（亦为 22 级）而不满足要求。

现有 mm 趟车次的运行情况（全部满足要求），试推算这nn 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：

第一行包含 22 个正整数 n, mn,m，用一个空格隔开。

第 i + 1i+1 行(1 ≤ i ≤ m)(1≤i≤m)中，首先是一个正整数 s_i(2 ≤ s_i ≤ n)si​(2≤si​≤n)，表示第ii 趟车次有 s_isi​ 个停靠站；接下来有s_isi​个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

一个正整数，即 nn 个火车站最少划分的级别数。

输入输出样例

输入样例#1： 

9 2 
4 1 3 5 6 
3 3 5 6 

输出样例#1： 

2

输入样例#2： 

9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9 

输出样例#2： 

3

说明

对于20\%20%的数据，1 ≤ n, m ≤ 101≤n,m≤10；

对于 50\%50%的数据，1 ≤ n, m ≤ 1001≤n,m≤100；

对于 100\%100%的数据，1 ≤ n, m ≤ 10001≤n,m≤1000。

拓扑排序概念

    这是一道拓扑排序的题

    拓扑排序是什么呢？

    对于一个有向无环图(Diricted Acyclic Graph,DAG)，对其全部节点，生成一个序列，来表达这个图的先后关系，这就是拓扑排序。

    如图：

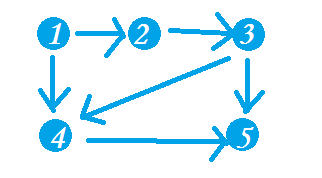
    就好像技能树或科技树一样：（顺便安利下这个环世界）

    

算法实现过程

    1）基本思想：以入度为0的点为基础，不断删边，减小其他点的入度，

    2）具体实现：

        1）初始化：把入度为0的点加入队列，并加入ans数组(记得加入ans，这是我踩过的坑)

        2）对于队列中的每个元素，广度遍历其出边：

            1）将元素取出并pop

            2）将出边连接点的入度减1

            3）如果其入度为0，则入队并加入ans数组

        3）直至队列空

代码：

#include<cstdio>
#include<queue>
#define MAX 10010
using namespace std;
struct Edge{
    int u,v,next;
}edge[MAX];
int first[MAX],n,m,cnt=0,rudu[MAX],ans[MAX];
void AddEdge(int u,int v){
    edge[++cnt].u=u;edge[cnt].v=v;edge[cnt].next=first[u];first[u]=cnt;
}
void topsort(){
    int bl=0;
    queue<int> q;
    for(int i=1;i<=n;i++)if(rudu[i]==0){q.push(i);ans[++bl]=i;}
    while(!q.empty()){
        int u=q.front();q.pop();
        int i=first[u];
        while(i!=-1){
            int v=edge[i].v;
            rudu[v]--;
            if(rudu[v]==0){
                ans[++bl]=v;
                q.push(v);
            }
            i=edge[i].next;
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)first[i]=-1;
    for(int i=1;i<=n;i++)rudu[i]=0;
    for(int i=1;i<=n;i++)ans[i]=-1;
    int X,Y;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&X,&Y);
        AddEdge(X,Y);
        rudu[Y]++;
    }
    topsort();
    for(int i=1;i<=n;i++){
        printf("%d ",ans[i]);
    }
    return 0;
}

     这样就结束了，美滋滋。