33. Search in Rotated Sorted Array

一、题目

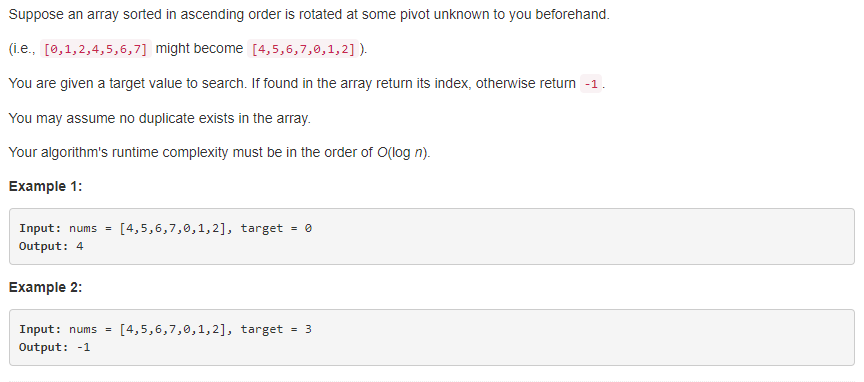
　　1、审题

　　　　

　　2、分析

　　　　给出一个有序的数组，其中循环向右移动了若干个单元，导致数组成了两个有序的模块。求 target 在数组中的下标，其中时间复杂度必须为 O（log n）.

二、解答

　　1、思路：

　　　　a、通过二分法求得数组中有序的两组数的分割开的下标；

　　　　b、通过二分法求 target 在两组有序数中的下标，若存在，则返回，否则返回-1.

class Solution {
    public int search(int[] nums, int target) {

        int len = nums.length;
        int low = 0;
        int high = len - 1;

        if(len == 0)
            return -1;

        while(low < high){  // 找到分界点， 用 low 记录
            int median = (low + high) / 2;

            if(nums[low] < nums[median])
                low = median;
            else if(nums[low] > nums[median])
                high = median;
            else {
                if(nums[low] < nums[high])
                    low = high;
                break;
            }
        }
        System.out.println("low=" + low);
        int index = binarySearch(nums, target, 0, low);
        if(index != -1)
            return index;

        index = binarySearch(nums, target, low+1, len-1);
        return index;
    }

    private  int binarySearch(int[] nums, int target, int low, int high) {
        // 二分
        int median = (high+low) / 2;
        while(low <= high) {

            if(nums[median] == target)
                return median;

            if(nums[median] > target) {
                high = median - 1;
            }
            else {
                low = median + 1;
            }
            median = (high+low) / 2;
        }
        return -1;
    }
}