tf1

来自 https://zhuanlan.zhihu.com/p/81677580

①Tensorflow——tf.placeholder

placeholder函数定义如下：

tf.placeholder(dtype, shape=None, name=None)

参数说明：

dtype：数据类型。常用的是tf.float32, tf.float64等数值类型。

shape：数据形状。默认是None，就是一维值。如果是多维的话，定义如下:[2,3], [None, 3]等。其中 [None, 3]表示列是3，行数不定。此参数可以根据提供的数据推导得到，不一定要给出。

name：名称。比如常在书中看到的x-input, y-input。

 

import tensorflow as tf
 
# 定义placeholder
input1 = tf.placeholder(tf.float32,shape=[1, 2],name="input-1")
input2 = tf.placeholder(tf.float32,shape=[2, 1],name="input-2")
 
# 定义矩阵乘法运算(注意区分matmul和multiply的区别：matmul是矩阵乘法，multiply是点乘)
output = tf.matmul(input1, input2)
 
# 通过session执行乘法运行
with tf.Session() as sess:
    # 执行时要传入placeholder的值
    print (sess.run(output, feed_dict = {input1:[1,2], input2:[3,4]}))
    # 最终执行结果 [11]

②Tensorflow——tf.reduce_mean()

求平均值：

tf.reduce_mean(input_tensor, reduction_indices=None, keep_dims=False, name=None)

• 参数1--input_tensor:待求值的tensor
• 参数2--reduction_indices:在哪一维上求解
• 参数3、4可忽略

import tensorflow as tf
sess = tf.InteractiveSession()

x = [[1., 2.], [3., 4.]]

mean1 = tf.reduce_mean(x) # 如果不指定第二个参数，那么就在所有的元素中取平均值
print(sess.run(mean1))

mean2 = tf.reduce_mean(x, 0) # 指定第二个参数为0，则第一维的元素取平均值，即每一列求平均值
print(sess.run(mean2))

mean3 = tf.reduce_mean(x, 1) # 指定第二个参数为1，则第二维的元素取平均值，即每一行求平均值
print(sess.run(mean3))

输出：

2.5
[2. 3.]
[1.5 3.5]

③Tensorflow——padding

一、图示说明

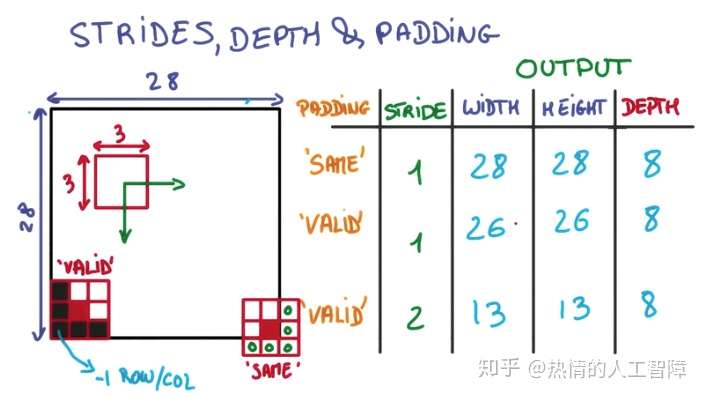
• 用一个3x3的网格在一个28x28的图像上做切片并移动
• 移动到边缘上的时候，如果不超出边缘，3x3的中心就到不了边界
• 因此得到的内容就会缺乏边界的一圈像素点，只能得到26x26的结果
• 而可以越过边界的情况下，就可以让3x3的中心到达边界的像素点
• 超出部分的矩阵补零

二、代码说明

根据tensorflow中的conv2d函数，我们先定义几个基本符号：

• 输入矩阵W×W，这里只考虑输入宽高相等的情况，如果不相等，推导方法一样，不多解释。
• filter矩阵F×F，卷积核
• stride值S，步长
• 输出宽高为new_height、new_width

在Tensorflow中对padding定义了两种取值：VALID、SAME。下面分别就这两种定义进行解释说明。

2.1 VALID

new_height = new_width = (W – F + 1) / S #结果向上取整

• 含义：new_height为输出矩阵的高度
• 说明：VALID方式不会在原有输入矩阵的基础上添加新的值，输出矩阵的大小直接按照公式计算即可

2.2 SAME

new_height = new_width = W / S #结果向上取整

• 含义：new_height为输出矩阵的高度
• 说明：对W/S的结果向上取整得到W"包含"多少个S

pad_needed_height = (new_height – 1) × S + F - W

• 含义：pad_needed_height为输入矩阵需要补充的高度
• 说明：因为new_height是向上取整的结果，所以先-1得到W可以完全包裹住S的块数，之后乘以S得到这些块数的像素点总和，再加上filer的F并减去W，即得到在高度上需要对W补充多少个像素点才能满足new_height的需求

pad_top = pad_needed_height / 2 #结果取整

• 含义：pad_top为输入矩阵上方需要添加的高度
• 说明：将上一步得到的pad_needed_height除以2作为矩阵上方需要扩充0的像素点数

pad_bottom = pad_needed_height - pad_top

• 含义：pad_bottom为输入矩阵下方需要添加的高度
• 说明：pad_needed_height减去pad_top的剩余部分补充到矩阵下方

以此类推，在宽度上需要pad的像素数和左右分别添加的像素数为：

pad_needed_width = (new_width – 1) × S + F - W

pad_left = pad_needed_width / 2 #结果取整

pad_right = pad_needed_width – pad_left

 

④Tensorflow——tf.nn.conv2d

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)

除去name参数用以指定该操作的name，与方法有关的一共五个参数：

1. input：指需要做卷积的输入图像，它要求是一个Tensor，具有[batch, in_height, in_width, in_channels]这样的shape，具体含义是[训练时一个batch的图片数量,图片高度,图片宽度,图像通道数]，注意这是一个4维的Tensor，要求类型为float32和float64其中之一；
2. filter：相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height, filter_width, in_channels, out_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，要求类型与参数input相同， 有一个地方需要注意，第三维in_channels，就是参数input的第四维；
3. 第三个参数strides：卷积时在图像每一维的移动步长，这是一个一维的向量，长度4；
4. 第四个参数padding：string类型的量，只能是"SAME","VALID"其中之一，这个值决定了不同的卷积方式（后面会介绍）；
5. 第五个参数：use_cudnn_on_gpu:bool类型，是否使用cudnn加速，默认为true。

结果返回一个Tensor，这个输出，就是我们常说的feature map。

import tensorflow as tf

#[batch, in_height, in_width, in_channels]
#[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]
input = tf.Variable(tf.random_normal([1, 4, 4, 5]))

#[filter_height, filter_width, in_channels, out_channels]
#[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]
filter = tf.Variable(tf.random_normal([3, 3, 5, 1]))

#padding的值为‘VALID’，表示边缘不填充,当其为‘SAME’时，表示填充到卷积核可以到达图像边缘
op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='SAME')
init = tf.global_variables_initializer()

with tf.Session() as sess:
     sess.run(init)
     print(sess.run(op))

 

⑤Tensorflow——sess.run()

sess.run()中的feed_dict

我们都知道feed_dict的作用是给使用placeholder创建出来的tensor赋值。其实，它的作用更加广泛：feed使用一个值临时替换一个op的输出结果。你可以提供feed数据作为run()调用的参数。feed只在调用它的方法内有效,方法结束,feed就会消失。

sess.run()

当我们构建完图后，需要在一个会话中启动图，启动的第一步是创建一个Session对象。

为了取回（Fetch）操作的输出内容，可以在使用Session对象的run()调用执行图时，传入一些tensor，这些tensor会帮助你取回结果。

在python语言中，返回的tensor是numpy ndarray对象。

在执行sess.run()时，tensorflow并不是计算了整个图，只是计算了与想要fetch的值相关的部分。

使用feed_dict字典填充

tensorflow还提供字典填充函数，使输入和输出更为简单：feed_dict = {}。

例如：需要把8和2填充到字典中，就需要占位符tensorflow.placeholder()而非变量，input1 = tf.placeholder(tf.float32)，因为是一个元素不需要矩阵相乘，只要简单的乘法即可：tensorflow.multiply()。

import tensorflow as tf
#设置两个乘数，用占位符表示
input1 = tf.placeholder(tf.float32)
input2 = tf.placeholder(tf.float32)
#设置乘积
output = tf.multiply(input1, input2)
with tf.Session() as sess:
  #用feed_dict以字典的方式填充占位
 print(sess.run(output, feed_dict={input1:[8.],input2:[2.]}))

结果是：

[ 16.]

占位符和feed_dict

import tensorflow as tf
import numpy as np

list_of_points1_ = [[1, 2], [3, 4], [5, 6], [7, 8]]
list_of_points2_ = [[15, 16], [13, 14], [11, 12], [9, 10]] 

list_of_points1 = np.array([np.array(elem).reshape(1, 2) for elem in list_of_points1_])
list_of_points2 = np.array([np.array(elem).reshape(1, 2) for elem in list_of_points2_])

graph = tf.Graph()

with graph.as_default():
#我们使用tf.placeholder()创建占位符 ，在session.run()过程中再投递数据
    point1 = tf.placeholder(tf.float32, shape=(1, 2))
    point2 = tf.placeholder(tf.float32, shape=(1, 2))

def calculate_eucledian_distance(point1, point2):
    difference = tf.subtract(point1, point2)
    power2 = tf.pow(difference, tf.constant(2.0, shape=(1, 2)))
    add = tf.reduce_sum(power2)
    eucledian_distance = tf.sqrt(add)
    return eucledian_distance

dist = calculate_eucledian_distance(point1, point2)

with tf.Session(graph=graph) as session:
    tf.global_variables_initializer().run()
    for ii in range(len(list_of_points1)):
        point1_ = list_of_points1[ii]
        point2_ = list_of_points2[ii]
        #使用feed_dict将数据投入到[dist]中
        feed_dict = {point1: point1_, point2: point2_}
        distance = session.run([dist], feed_dict=feed_dict)
        print("the distance between {} and {} -> {}".format(point1_, point2_, distance))

输出：

the distance between [[1 2]] and [[15 16]] -> [19.79899]
the distance between [[3 4]] and [[13 14]] -> [14.142136]
the distance between [[5 6]] and [[11 12]] -> [8.485281]
the distance between [[7 8]] and [[ 9 10]] -> [2.828427]

⑥Tensorflow——epochs，batch_size，iterations

batch

深度学习的优化算法，说白了就是梯度下降。每次的参数更新有两种方式。

第一种，遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍，计算量开销大，计算速度慢，不支持在线学习，这称为Batch gradient descent，批梯度下降。

另一种，每看一个数据就算一下损失函数，然后求梯度更新参数，这个称为随机梯度下降，stochastic gradient descent。这个方法速度比较快，但是收敛性能不太好，可能在最优点附近晃来晃去，hit不到最优点。两次参数的更新也有可能互相抵消掉，造成目标函数震荡的比较剧烈。

为了克服两种方法的缺点，现在一般采用的是一种折中手段，mini-batch gradient decent，小批的梯度下降，这种方法把数据分为若干个批，按批来更新参数，这样，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不是很大。

基本上现在的梯度下降都是基于mini-batch的，所以深度学习框架的函数中经常会出现batch_size，就是指这个。

iterations

iterations（迭代）：每一次迭代都是一次权重更新，每一次权重更新需要batch_size个数据进行Forward运算得到损失函数，再BP算法更新参数。1个iteration等于使用batchsize 个样本训练一次。

epochs

epochs被定义为向前和向后传播中所有批次的单次训练迭代。这意味着1个周期是整个输入数据的单次向前和向后传递。简单说，epochs指的就是训练过程中数据将被“轮”多少次，就这样。

举个例子

训练集有1000个样本，batchsize=10，那么：
训练完整个样本集需要：
100次iteration，1次epoch。

具体的计算公式为：
one epoch = numbers of iterations = N = 训练样本的数量/batch_size

注：

在LSTM中我们还会遇到一个seq_length,其实
batch_size = num_steps * seq_length

 

⑦Tensorflow——Tensorboard

1. 运行整个程序，在程序中定义的summary node就会将要记录的信息全部保存在指定的logdir路径中了，训练的记录会存一份文件，测试的记录会存一份文件。

checkpointFile = 'NewCheckpoints/Checkpoint3.ckpt'
#各种构建模型graph的操作(矩阵相乘，sigmoid等等....)
sess = tf.InteractiveSession()  # 加载它自身作为默认构建的session
saver = tf.train.Saver()  # 生成saver
sess.run(tf.initialize_all_variables())  # 先对模型初始化
#然后将数据丢入模型进行训练
#训练完以后，使用saver.save来保存
save_path = saver.save(sess, checkpointFile)

2. 进入linux命令行，运行以下代码，等号后面加上summary日志保存的路径。

tensorboard --logdir=

我的summary日志保存在NewCheckpoints。

路径为：/Users/siyuchou/PycharmProjects/DQN_PathPlanning/NewCheckpoints

执行命令之后会出现一条信息，然后打开

http://192.168.1.100:6006

就可以看到我们定义的可视化信息了。

 

⑧Tensorflow——tf.reshape

tf.reshape(tensor, shape, name=None)

函数的作用是将tensor变换为参数shape的形式。

其中shape为一个列表形式，特殊的一点是列表中可以存在-1。-1代表的含义是不用我们自己指定这一维的大小，函数会自动计算，但列表中只能存在一个-1。（当然如果存在多个-1，就是一个存在多解的方程了）

#tensor 't' is [1, 2, 3, 4, 5, 6, 7, 8, 9]
#tensor 't' has shape [9]
reshape(t, [3, 3]) ==> [[1, 2, 3],[4, 5, 6],[7, 8, 9]]

#tensor 't' is [ [[1, 1], [2, 2]] , [[3, 3], [4, 4]] ]
#tensor 't' has shape [2, 2, 2]
reshape(t, [2, 4]) ==> [[1, 1, 2, 2],[3, 3, 4, 4]]

#tensor 't' is [ [[1, 1, 1],[2, 2, 2]] , [[3, 3, 3],[4, 4, 4]] , [[5, 5, 5],[6, 6, 6]] ]
#tensor 't' has shape [3, 2, 3]
#pass '[-1]' to flatten 't'
reshape(t, [-1]) ==> [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6]
#-1 can also be used to infer the shape
#-1 is inferred to be 9:
reshape(t, [2, -1]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],[4, 4, 4, 5, 5, 5, 6, 6, 6]]
#-1 is inferred to be 2:
reshape(t, [-1, 9]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],[4, 4, 4, 5, 5, 5, 6, 6, 6]]
#-1 is inferred to be 3:
reshape(t, [2, -1, 3]) ==> [ [[1, 1, 1],[2, 2, 2],[3, 3, 3]] , [[4, 4, 4],[5, 5, 5],[6, 6, 6]] ]

#tensor 't' is [7]
#shape `[]` reshapes to a scalar
reshape(t, []) ==> 7

 

⑨Tensorflow—— tf.train.AdamOptimizer

此函数是Adam优化算法：是一个寻找全局最优点的优化算法，引入了二次方梯度校正。相比于基础SGD算法：

1. 不容易陷于局部优点
2. 速度更快，学习效果更为有效
3. 纠正其他优化技术中存在的问题，如学习率消失或是高方差的参数更新导致损失函数波动较大等问题。

Adam这个名字来源于Adaptive Moment Estimation，自适应矩估计。

概率论中矩的含义是：如果一个随机变量 服从某个分布， 的一阶矩是 ，也就是样本平均值， 的二阶矩就是 ，也就是样本平方的平均值。

Adam算法根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对于每个参数的学习速率。

 

⑩Tensorflow —— tf.train.exponential_decay

在Tensorflow中，为解决设定学习率(learning rate)问题，提供了指数衰减法来解决。

通过tf.train.exponential_decay函数实现指数衰减学习率。

1. 步骤：

• 首先使用较大学习率(目的：为快速得到一个比较优的解);
• 然后通过迭代逐步减小学习率(目的：为使模型在训练后期更加稳定);

2. 代码实现：

decayed_learning_rate=learining_rate*decay_rate^(global_step/decay_steps)

其中：

• decayed_learning_rate为每一轮优化时使用的学习率；
• learning_rate为事先设定的初始学习率；
• decay_rate为衰减系数；
• decay_steps为衰减速度。

而tf.train.exponential_decay函数则可以通过staircase(默认值为False)选择不同的衰减方式：如果staircase = True，那就表明每decay_steps次计算学习速率变化，更新原始学习速率，如果是False，那就是每一步都更新学习速率。红色表示False，绿色表示True。

global_step = tf.Variable(0)
learning_rate = tf.train.exponential_decay(0.1, global_step, 100, 0.96, staircase=True) #生成学习率
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(....., global_step=global_step)  #使用指数衰减学习率

learning_rate：0.1；

staircase = True；

则每100轮训练后要乘以0.96。

通常初始学习率，衰减系数，衰减速度的设定具有主观性(即经验设置)，而损失函数下降的速度与迭代结束之后损失的大小没有必然联系，所以神经网络的效果不能单一的通过前几轮损失函数的下降速度来比较。

 

11.Tensorflow——as_default():

 

作用：

返回一个上下文管理器，使得这个Graph对象成为当前默认的graph。当你想在一个进程里面创建多个图的时候，就应该使用这个函数。为了方便起见，一个全局的图对象被默认提供，要是你没有显式创建一个新的图的话，所有的操作(ops) 都会被添加到这个默认的图里面来。

通过with关键字和这个方法，来让这个代码块内创建的从操作(ops) 添加到这个新的图里面。

默认的是当前线程的“property”，如果你创建了一个新的线程而且想使用这个默认的图，你应该显式添加一个g.as_default():在这个线程函数里面。

下面是两种写法示例：

# 1. Using Graph.as_default():
g = tf.Graph()
with g.as_default():
    c = tf.constant(5.0)
    assert c.graph is g

# 2. Constructing and making default:
with tf.Graph().as_default() as g:
    c = tf.constant(5.0)
    assert c.graph is g

 

12.Tensorflow——tf.reduce_sum()

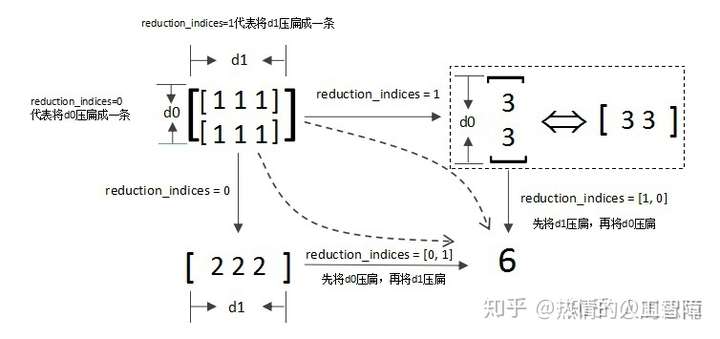
调用reduce_sum(arg1, arg2)时，参数arg1即为要求和的数据，arg2有两个取值分别为0和1，通常用reduction_indices=[0]或reduction_indices=[1]来传递参数。

• 当arg2 = 0时，是纵向对矩阵求和，原来矩阵有几列就得到几个值；
• 当arg2 = 1时，是横向对矩阵求和；
• 当省略arg2参数时，默认对矩阵所有元素进行求和。

看到这里，函数名的前缀为什么是reduce其实也就很容易理解了，reduce就是“对矩阵降维”的含义，下划线后面的部分就是降维的方式，在reduce_sum()中就是按照求和的方式对矩阵降维。那么其他reduce前缀的函数也举一反三了，比如reduce_mean()就是按照某个维度求平均值，等等。

 

13.Tensorflow——tf.global_variables_initializer()

global_variables_initializer返回一个用来初始化计算图中所有global variable的op。

这个op到底是啥，还不清楚。

函数中调用了variable_initializer()和global_variables()

global_variables()返回一个Variable list，里面保存的是gloabal variables。

variable_initializer()将Variable list中的所有Variable取出来，将其variable.initializer属性做成一个op group。

然后看Variable类的源码可以发现， variable.initializer就是一个assign op。

所以： sess.run(tf.global_variables_initializer()) 就是run了所有global Variable的assign op，这就是初始化参数的本来面目。

 

14.Tensorflow——tf.train.Saver()

https://blog.csdn.net/qiqiaiairen/article/details/53184216​blog.csdn.net

15.Unsuccessful TensorSliceReader constructor

https://blog.csdn.net/u014283248/article/details/64440019​blog.csdn.net

16.Tensorflow——tf.concat()

https://blog.csdn.net/mao_xiao_feng/article/details/53366163​blog.csdn.net

17.TensorLow:FailedPreconditionError

https://blog.csdn.net/shaozhulei555/article/details/78469883​blog.csdn.net

18.TensorFlow可视化卷积层

11 使用Tensorboard显示图片​www.cnblogs.com用TensorFlow可视化卷积层的方法​nooverfit.comhttps://blog.csdn.net/u014038273/article/details/78618500​blog.csdn.netTool request: Deep Visualization Toolbox for TensorFlow · Issue #842 · tensorflow/tensorflow​github.com

19.Tensorflow——Softmax函数

神经网络解决多分类问题最常用的方法是设置 个输出节点，其中 为类别的个数。对于每一个样例，神经网络可以得到一个 维数组作为输出结果。数组中的每一个维度（也就是每一个输出节点）对应一个类别，通过前向传播算法得到的输出层每个维度值代表属于这个类别的可能性大小。

也就是说，任意事件发生的概率都在0和1之间，且总有某一个事件发生（概率的和为1）。如果将分类问题中“一个样例属于某一个类别”看成一个概率事件，那么训练数据的正确答案就符合一个概率分布。如何将神经网络前向传播得到的结果也变成概率分布呢？Softmax回归就是一个非常常用的方法。

Softmax回归本身可以作为一个学习算法来优化分类结果，它只是神经网络中的一层额外的处理层，将神经网络的输出变成了一个概率分布，下图展示了加上了Softmax回归的神经网络结构图。

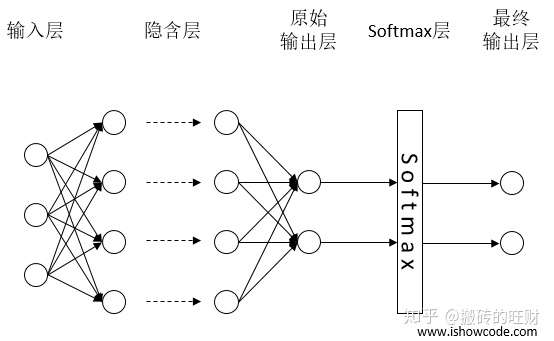通过softmax层将神经网络输出变成一个概率分布

假设原始的神经网络输出为 , , …, ,那么经过Softmax回归处理之后的输出为：

从以上公式中可以看出，原始神经网络的输出被用作置信度来生成新的输出，而新的输出满足概率分布的所有要求。这个新的输出可以理解为经过神经网络的推导，一个样例为不同类别的概率分别是多大。这样就把神经网络的输出也变成了一个概率分布，从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了。

下面我们通过一个浅层神经网络来描述此过程，如下图所示：

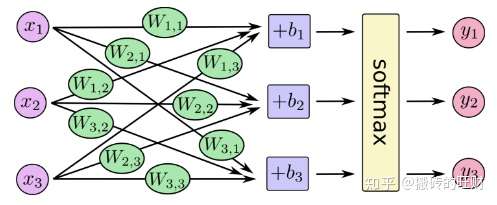
我们可以将此过程写成一个等式：

我们可以将上述过程向量化，将其转成矩阵相乘和向量相加，这样有助于提高运算效率。

发布于 2019-09-08