一,欧拉函数
定义:不超过n的且与n互质的正整数的个数。
1.如果n为素数,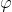 (n)=n-1;
(n)=n-1;
因为素数p的质因数只有1和它本身,p和p不为互质,所以φ(p)=p-1;
2.如果n为某一个素数p的幂次,那么φ(p^a)=(p-1)*p^(a-1);
因为比p^a小的数有p^a-1个,那么有p^(a-1)-1个数能被p所整除(因为把1~p^a-1的p的倍数都筛去了)
所以φ(p)=p^a-1-(p^(a-1)-1)=(p-1)*p^(a-1);
3.如果n为任意两个数a和b的积,那么φ(a*b)=φ(a)*φ(b)
欧拉函数为乘性函数(积性函数)
定义1:如果函数对任意两个互质的正整数n,m,均有
.就称
为乘性函数(积性函数);
定义2:如果函数对任意两个正整数n,m,均有
.就称
为完全乘性函数(完全积性函数);
因为比a*b小的数有a*b-1个,条件是a与b互质
那么可以知道,只有那些既满足a与其互质且既满足b与其互质的数满足条件。
根据乘法原理,这样的数可以互相组合,那么就有φ(a)*φ(b)个
所以可以得知φ(a*b)=φ(a)*φ(b) (注意条件必须满足a和b互质)
4.设n=(p1^a1)*(p2^a2)*……*(pk^ak) (为N的分解式)
那么φ(n)=n*(1-1/p1)*(1-1/p2)*……*(1-1/pk)
因为各个分解完的p1、p2、……pk均为素数,所以它们均为互质的
每次再刨去它们本身,乘起来, 剩下的运用容斥原理,再根据引理2和引理3就可以得出
二,欧拉定理:
a^(φ(m)) ≡1(mod m) (a与m互质)
三【欧拉函数的通式】
φ(n)=n*(1-1/p1)*(1-1/p2)*(1-1/p3)*(1-1/p4)…..(1-1/pn)
通式求欧拉函数
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll oula(ll n){
ll ans=n;
for(int i=2;i*i<=n;i++){
if(n%i==0) {
ans=ans-ans/i;//欧拉函数通式
while(n%i==0){//消除i因子
n/=i;
}
}
}
cout<<n<<endl;
if(n>1) ans=ans-ans/n;//n>1,说明存在一个素因子没除,例如46;
return ans;
}
int main()
{
ll n;
scanf("%lld",&n);
ll ans=oula(n);
cout<<ans<<endl;
return 0;
}
一种筛选方法
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
ll phi[maxn];
void getoula(ll n){
for(int i=2;i<=n;i++){
phi[i]=0;
}
phi[1]=1;
for(int i=2;i<=n;i++){
if(!phi[i]){
for(int j=i;j<=n;j+=i){
if(!phi[i]) phi[j]=j;
phi[j]=phi[j]/i*(i-1);
}
}
}
}
int main()
{
ll n;
scanf("%lld",&n);
ll ans=oula(n);
cout<<ans<<endl;
return 0;
}欧拉函数的线性筛法
大家都知道素数的线性筛法吧,欧拉函数也有线性筛法,可以在线性时间内求出1~N的所有φ
有以下三条性质:
①:φ(p)=p-1
②:φ(p*i)=p*φ(i) (当p%i==0时)
③:φ(p*i)=(p-1)*φ(i) (当p%i!=0时)
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
ll phi[maxn];
ll prime[maxn];
bool v[maxn];
int x;
void getphi(int n){
phi[1]=1;
for(int i=2;i<=n;i++){
if(!v[i]){
prime[x++]=i;
phi[i]=i-1;
}
for(int j=0;j<x;j++){
if(i*prime[j]>n){
break;
}
v[i*prime[j]]=true;
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else {
phi[i*prime[j]]=phi[i]*phi[prime[j]];
}
}
}
}
int main()
{
ll n;
scanf("%lld",&n);
getphi(n);
for(int i=1;i<=n;i++){
cout<<phi[i]<<endl;
}
return 0;
}