1161 Maximum Level Sum of a Binary Tree 最大层内元素和
描述
给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
请你找出层内元素之和 最大 的那几层(可能只有一层)的层号,并返回其中 最小 的那个。
- 示例:
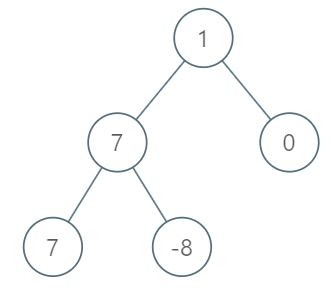
输入:[1,7,0,7,-8,null,null]
输出:2
解释:
第 1 层各元素之和为 1,
第 2 层各元素之和为 7 + 0 = 7,
第 3 层各元素之和为 7 + -8 = -1,
所以我们返回第 2 层的层号,它的层内元素之和最大。
- 提示:
- 树中的节点数介于 1 和 10^4 之间
-10^5 <= node.val <= 10^5
思路
-
读题
- 层内元素和 返回层内元素和最大的那层层号 root节点为第1层
如果最大元素和有多个 返回最小层号
- 层内元素和 返回层内元素和最大的那层层号 root节点为第1层
-
这是一个
二叉树BFS问题
需要计算每一层的节点
注意: 这也可以是二叉树DFS问题, 只要给DFS加上深度标号即可 -
可以使用队列Queue来交替存储父节点和子节点 从而实现按层遍历
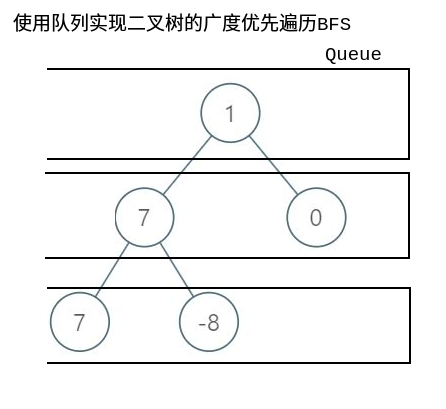
代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxLevelSum(TreeNode root) {
if (null == root) return -1;
// q 父节点队列 存储当前遍历节点
Queue<TreeNode> q = new LinkedList<>();
// t 子节点队列 存储当前遍历节点的子节点
Queue<TreeNode> t = new LinkedList<>();
// 队列压入根节点
q.offer(root);
// maxSum 最大层内元素和
int maxSum = 0;
// maxLevel 最大层内元素和的层号
int maxLevel = 0;
// cur 当前层内元素和
int cur = 0;
// level 当前层号
int level = 0;
while (!q.isEmpty()) {
TreeNode curnode = q.poll();
cur += curnode.val;
if (curnode.left != null) t.offer(curnode.left);
if (curnode.right != null) t.offer(curnode.right);
// 当该层遍历完
if (q.isEmpty()) {
// 层号+1
level++;
// 当前层内元素和 > 最大层内元素和 ?
if (maxSum < cur) {maxSum = cur; maxLevel = level;}
// 遍历的队列交替
cur = 0; q = t; t = new LinkedList<>();
}
}
return maxLevel;
}
}