引言
KMP算法应该是看了一次又一次,比赛的时候字符串不是我负责,所以学到的东西又还给网上的博客了……
退役后再翻开看,看到模板,心想这不是(O(n^2))的复杂度吗?
有两个循环也不能看做是(O(n^2))的,这要用到摊还分析.
模板
这里用到的模板是算竞上的
calc_next()
Next[1] = 0;
for (int i = 2, j = 0; i <= n; ++i) {
while (j > 0 && a[i] != a[j + 1]) j = Next[j];
if (a[i] == a[j + 1]) ++j;
Next[i] = j;
}
kmp()
for (int i = 1, j = 0; i <= m; ++i) {
while (j > 0 && (j == n || b[i] != a[j + 1]))j = Next[j];
if (b[i] == a[j + 1])++j;
f[i] = j;
}
可以发现上下两个函数挺像的,Next[i]含义就是模式串以(i)结尾的子串([1..i]的后缀)与模式串的前缀能匹配的最长长度
证明
观察发现有两个操作:
- 匹配成功:
j++,这个代价是1 - 匹配失败:
j=Next[j]还要经过while循环,这个代价未知
根据记账法,假设每个平摊代价是2,对于每个匹配成功的操作,其中1元用来j++,另1元就存起来,给后面匹配失败时用:
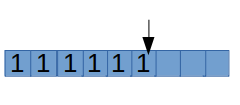
而当失配的时候,就会用到银行存款,最坏的情况当然就是用光了所有存款,但可以发现每个匹配的操作分配两个时间代价是完全足够的
换句话说,你使用存款肯定得要求银行有存款,而每次j++操作都会存1元,在当前j前面必然每个位置都是有大于等于1的存款
所以复杂度就是j++次数的两倍,也就是匹配串的长度 (2n)
根据平摊分析要求(check c_i ge c_i),平摊代价设置为(2)是完全满足的
综上所述:KMP算法两个函数的总体运算次数为(2n+2m),复杂度是(O(n+m))
总结
也不知道这样分析对不对,如果只是感性理解的话足够了.
也有势能法的做法,但是这样的话就要定义势能函数,我觉得记账法还是好理解一点.