图形是怎么生成的?
视频控制器通过访问帧缓存来刷新屏幕
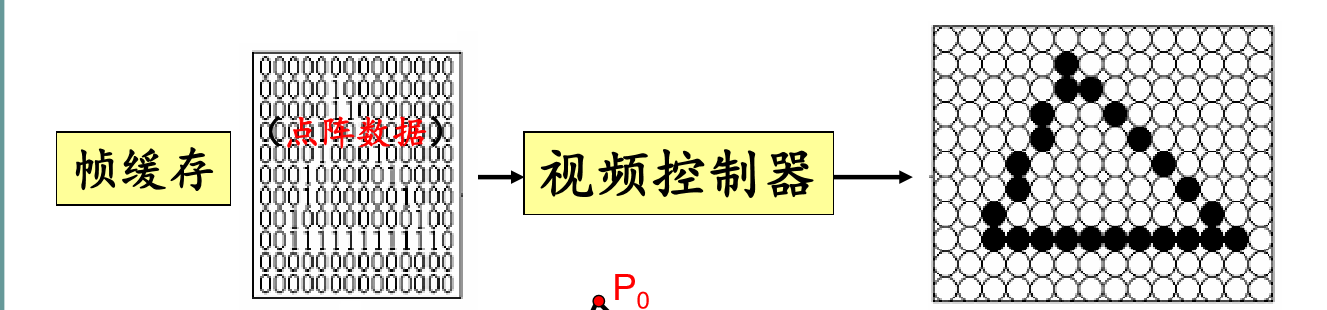
帧缓存中的保存的是点阵数据,而我们将要讨论的是
如何将图形的几何参数来得到点阵数据,本文主要介绍最简单的直线生成算法
通过两个点(p_0),(p_1),如何转化成帧缓存中的点阵数据
图元的生成
-
概念:图元的参数表示形式到点阵表示形式的转换
-
参数表示形式由不同种类图形的性质决定
-
点阵表示形式是光栅显示系统刷新时所需的表示形式。
在光栅显示器的荧光屏上生成一个对象,实质上是往帧暂存寄存器的相应单元中填入数据
-
像素操作函数:最基本的绘图函数,等同于写读帧缓存
- 写像素:
SetPixel ( int x, int y, int color ) - 读像素:
int GetPixel ( int x, int y)
- 写像素:
-
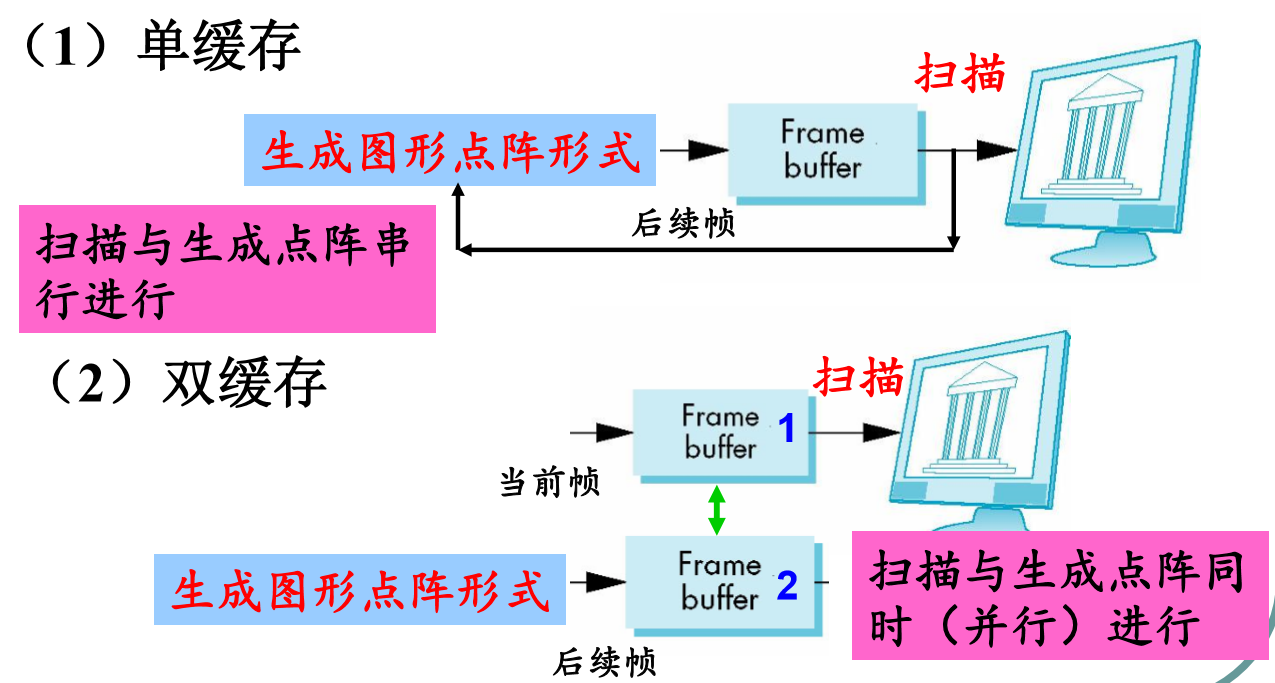
单缓存与双缓存:
直线生成的基本思路
画一条从(p_0)到$p_1 $的直线,实质上是一个发现最佳逼近直线的像素序列、并填入色彩数据的过程,这个过程也称为直线光栅化。
- 概念:求与直线段充分接近的像素集,并以此像素集替代原连续直线段在屏幕上显示。
说到直线,肯定想到最基础的直线方程(y=kx+b)。如果用这种方法,会用到乘法,加法,还有取整。最简单的找到充分接近的像素的方法就是取整。
这在计算机中效率是比较低的。
我们做一次改进:变乘法为加法
又因为(y_i=kx_i+b),所以
这样我们就可以通过递推式的方法解决问题。
基本增量算法(DDA)
-
基本思想:舍入法求解最佳逼近;利用微分思想,即每一个点坐标都可以由前一个坐标变化一个增量得到。
-
乘法用加法实现,每一个点坐标都可以由前一个坐标变化一个增量得到。
[x_{i+1}=x_i+Delta x ][y_{i+1}=y_i+Delta y ][Delta=t_{i+1}-t_i ] -
该算法在x或y变化比较大的方向的增量绝对值为1,而另一方向上的增量绝对值小于等于1。
-
为了方便,我们设置:(Delta x=1,Delta y=0.5)
-
实现代码,下面代码有多处错误:
//k在0到1之间
void LineDDA(int x0,int y0,int x1,int y1,int color){
int x, dx, dy, y; float k;
dx = x1 - x0; dy = y1 - y0; k = dy / dx; y = y0;
for(x = x0; x <= x1; x++) {
y = (int)(y + 0.5); SetPixel(x, y, color); y += k;
}
}
- 改错:
//k在0到1之间
void LineDDA(int x0,int y0,int x1,int y1,int color){
int x, dx, dy;
//y应该是浮点型
float k,y;
dx = x1 - x0; dy = y1 - y0;
//需要强制转换
k =(float)dy / dx;
y = y0;
for(x = x0; x <= x1; x++) {
// y = (int)(y + 0.5); SetPixel(x, y, color);
// 不应该先取整,这样会有很大误差。
SetPixel(x, (int)(y + 0.5), color);
y += k;
}
}
中点算法
-
目标:消除DDA算法中的浮点运算,浮点数取整运算,不利于硬件实现; DDA算法效率低。会不会有另外一种递推的方法?
-
直线隐式方程
[F(x,y)=ax+by+c=0 ]其中: (a = y_0-y_1= -Delta y, b = x_1-x_0= Delta x, c = x_0*y_1- x_1*y_0)
-
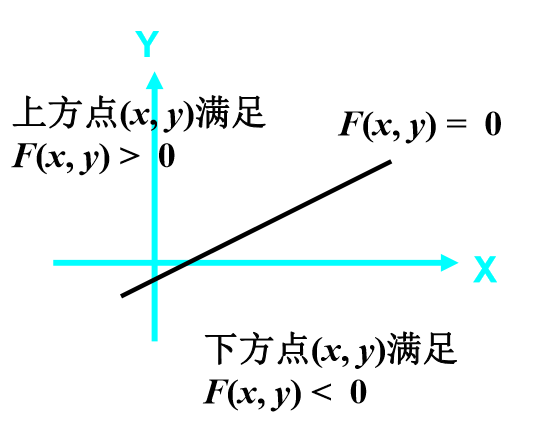
直线的正负划分性
- 直线上方的点:(F(x, y) >0)
- 直线下方的点:(F(x, y) <0)
- 直线上的点: (F(x, y) =0)
-
设:(y_i) 为实际坐标; (y_{i, r}) 表示取整后的坐标; (M)是中点
一、已计算出像素((x_i , y_{i,r}))如何判断距直线最近的下一个像素点
答案是根据可能所取点间的中点(M)与直线的位置
如果(M)在直线下方,那就选择像素点(NE),否则选择(E)
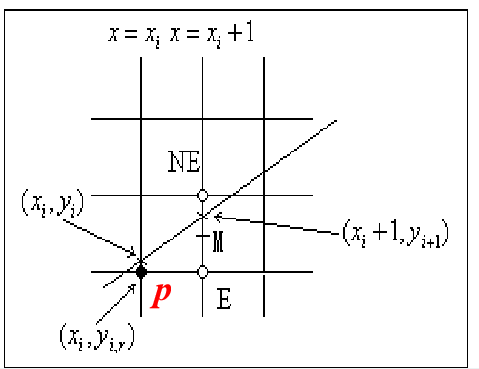
通过构造判别式:(d = F(M) = F(x_{i}+1, y_{i,r}+0.5)) 由(d) 的正和负可判定下一个像素
二、如何判定再下一个像素((x_i+2,??))
- 若(d≥0),取正右方像素(E),则判定再下一个像素的(d)为 (d_1= F(x_i+2, y_{i,r}+0.5) = a(x_i+2) + b(y_{i,r}+0.5) + c = d + a), (d)的增量是(a)(即(-Delta y))
- 若(d<0),取右上方像素(E),则判定再下一个像素的(d)为 (d_2= F(x_i+2, y_{i,r}+1.5) = d + a+b) , (d)的增量为(a+b) (即(-(Delta y-Delta x)))
三、增量(d_0)的初始值:
但是(F(x_0,y_0)=0),所以:
四、增量(d)的递推公式
五、优化:增量都是整数,只有初始值包含小数,可以用(2d)代替 (d), (2a)改写成(a + a)
/*x0<x1,y0<y1,0<=k<=1*/
void MidpointLine(int x0,int y0, int x1,int y1, int color){
int a,b,d1,d2,d,x,y;
a = y0 - y1;
b = x1 - x0;
d = a + a + b;
d1 = a + a;
d2 = (a + b) + (a + b);
x = x0;
y = y0;
SetPixel(x, y, color);
while (x<x1){
if (d<0){
y++;
d += d2;
}
else
d += d1;
x++ ;
SetPixel(x,y, color);
}
}
我们可以直接通过(d=F(M))的增量来构造递推式,从而:
1、不必计算直线之斜率,因此不做除法;
2、不用浮点数,只用整数;
3、只做整数加减法和乘2运算,而乘2运算可以用硬件移位实现。
其他情况
上文的递推式子只是当(0 leq m leq 1) 的时候会满足
这是因为(x)每次的变化量比(y)大,所以(y)每次最多增加(1)
例如:(p_0(0,0))和(p_1(6,12)),如果按照上面的递推式,得到的结果如下图绿线是:
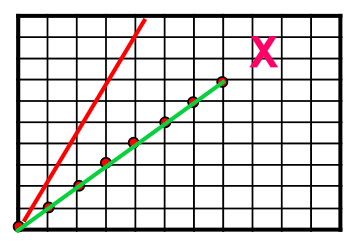
红线才应该是正确的。
- 当(0 leq m leq 1) :
(d_i < 0) 时(y)增加(1)
- 当(mgeq 1):
(d_i > 0) 时(x)增加(1)
- 当(-1 leq m leq 0):
(d_i>0)时(y)减少(1)
- 当(mleq 0):
(d_i<0)时(x)增加1
记住了第一个,其他都是同理
参考
[1] https://www.cnblogs.com/wkfvawl/p/11621653.html
[2] 老师课件