在测量转速时，我们经常会看到在方波脉冲的转折处信号出现明显的振荡，如图1所示。另外在进行锤击试验时，有的时候力脉冲也会在脉冲的末端位置出现振荡，如图2所示。我们已经知道力脉冲出现振荡现象称之为“振铃现象”。那么，为什么会在信号的转折处出现振铃现象呢？在回答这个问题之前，我们仔细观察一下这两个信号的时域特征，可以看出这两个信号在转折处都存在阶跃突变。
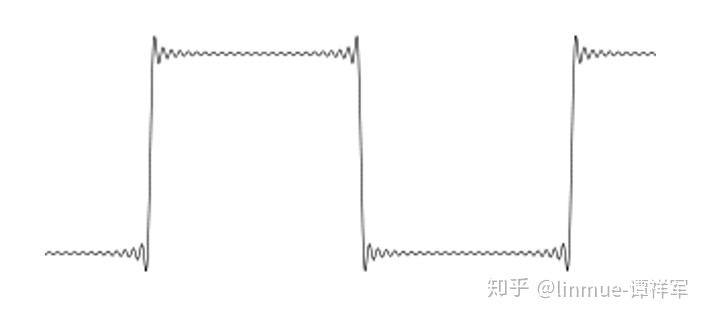图1 方波信号在转折处出现振荡(图片来自维基百科)
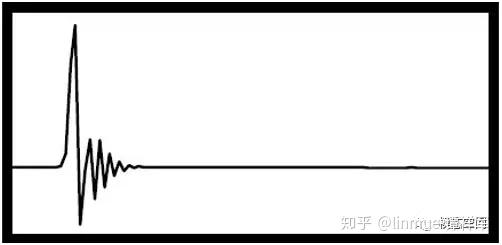图2 力脉冲在末端处出现振荡
1 背景
在《什么是泄漏？》一文中，我们讲到对信号进行FFT处理时，需要做截断，而截断又分为周期截断和非周期截断。假设原始信号是单频正弦波，如果截断的时间长度刚好是信号周期的整数倍，那么，截断后的每帧数据仍是周期信号，可重构得到原始的周期信号，如图3所示。此时，信号的频谱为单一频率的线状谱，如图4所示。
图3 周期截断
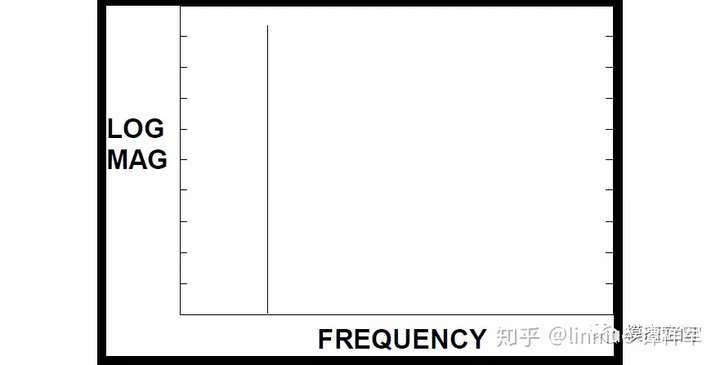图4 正弦信号正确的频谱
倘若信号截断的时间长度不为原始正弦信号周期的整数倍，那么，截断后的信号则不为周期信号。对同一个正弦信号进行非周期截断，如图5所示，截断后的信号起始时刻和结束时刻的幅值明显不等，将这个信号再进行重构，在连接处信号的幅值不连续，出现阶跃，如图5中黑色圆圈区域所示。对这个信号进行FFT分析，得到的频谱如图6所示，不再是正确的线状谱了，而是出现了明显的频率拖尾效应，频率成分分布在整个频带上了。
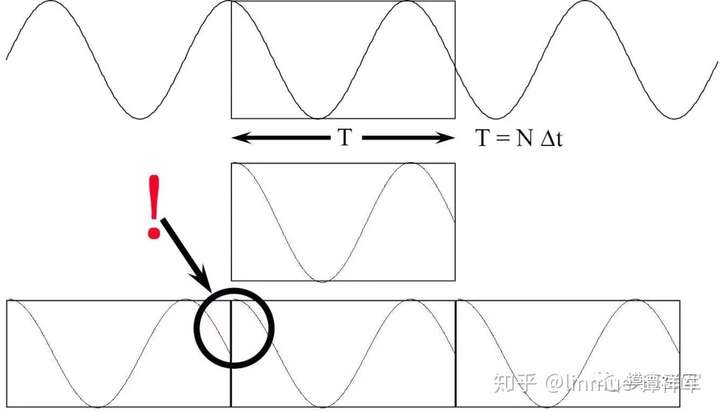图5 非周期截断
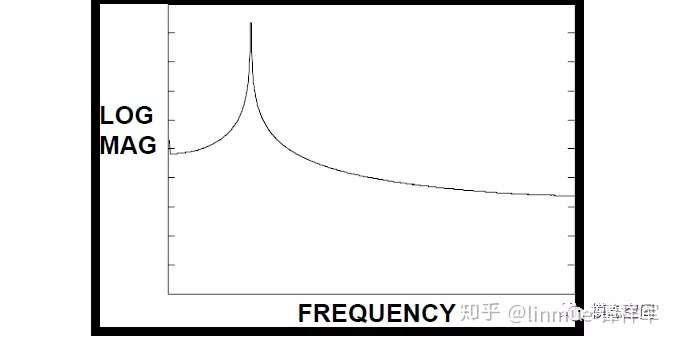图6 非周期截断导致频谱拖尾
根据傅里叶变换理论，任何一个信号都可认为是一系列正弦波之和。对于一个单频正弦波而言，使用傅里叶级数中的一项就可以描述了，形如Asinωt。但是对于一些信号，比如矩形脉冲信号，傅里叶级数要包含很多项，才能近似这个信号，这是因为矩形脉冲信号不连续，不像平滑的正弦波。因此，需要多个傅里叶展开项（多条谱线）去近似明显不连续的信号。现实世界中，一些常见的信号实例如图7所示。
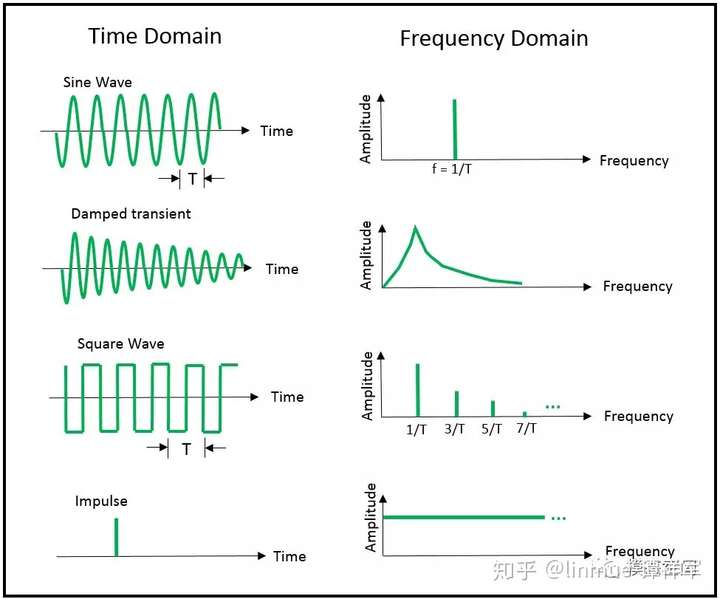图7 各种不同的时域信号（左）和它对应的频率成分（右）
对于图7所示的信号，注意到方波和脉冲信号具有无穷的频率成分。这两个信号都有存在不连续或突然阶跃的情况。对于这种突然瞬间改变的信号，它具有无穷的频率成分，使用有限频率带宽的数据采集系统是很难重现它们的。这就给测量系统增加了出现吉布斯现象的风险。接下来，我们讲讲什么是吉布斯现象。
2 吉布斯现象
在时域描述一个不连续的信号要求信号有无穷的频率成分。但实际情况是不可能采集到无穷的频率成分。信号采集系统只能采集一定频率范围内的信号，这将导致出现频率截断，频率截断会引起时域信号产生“振铃效应”，这个现象称之为吉布斯现象，如图1和图2所示。
任何突然不连续或阶跃信号总是会存在出现吉布斯现象，在这，我们使用一个方波信号来说明。现实世界中可能展示出吉布斯现象的信号包括汽车驶过坑时产生的冲击、力脉冲、爆炸声或者高尔夫球杆击球时产生的振动等等。
Josiah Willard Gibbs(1839-1903)是美国耶鲁大学的科学家，1899年，他在《自然》杂志上发表了关于一个阶跃函数的傅里叶级数中的过冲与下冲，这就是后来知名的“吉布斯现象”。后来发现到这个现象其实已经被英国数学家Henry Wilbraham在1848发现了。尽管这样，这个现象还是以吉布斯的名字命名。吉布斯是美国第一位工程学博士，他专攻数学物理学，他的工作影响了从化学热力学到物理光学等多个领域。
图8 Josiah Willard Gibbs
吉布斯现象体现在测量的时域信号的阶跃/转折位置出现振铃效应，如图9所示。
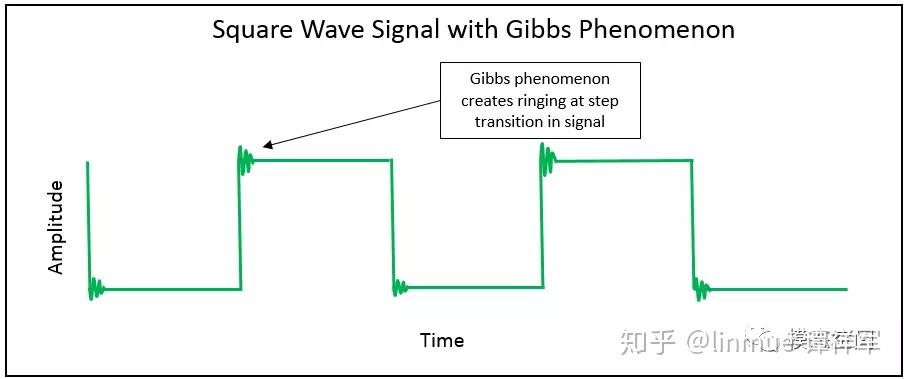图9 方波中的吉布斯现象
在数字信号采集系统中，在信号的每一个阶跃处，振铃使得信号出现不一致。信号的幅值出现变化或者完全不变化，这依赖于信号的瞬变时刻与数据采样点数的相对关系。
当使用少于合适数目的频率成分来描述信号时，就会产生振铃效应。图10用不同数量的正弦波来描述方波信号，可以看出，随着正弦波数量的增加，叠加后的信号越来越接近方波信号，振铃现象越来越弱，振荡的幅值越来越小，持续时间越来越短，信号的斜率越来越陡峭。
图10 随着正弦波数据的增加，吉布斯现象在减弱(图片来自维基百科)
现实中，经常有一些情况会少于理想数目的频率成分。
- 频率截断：测量系统不可能测量无穷的频率带宽。譬如，一个方波信号应包含无穷的谐波频率成分，当测量一个方波信号时，是不可能测量到无穷的谐波频率成分，信号总会出现频率截断。
- 滤波器形状：滤波器（如抗混叠滤波器）是测量系统经常要用的工具，它能引入与滤波器锐度相关的振铃效应。
在时域信号的每一个不连续处或阶跃处，围绕原始信号会出现过冲与下冲振铃。从幅值角度来看，时域信号的振铃并不总是想要的，会导致测量得到的幅值与实际信号的幅值存在差异。
3 吉布斯现象产生的原因与控制
从两个方面来描述吉布斯现象产生的振铃效应：
- 幅值：原始信号中有多大的过冲与下冲；
- 持续时间：振铃现象持续多长的时间。
这两个量说明如图11所示。
图11 吉布斯现象的振铃效应的幅值与持续时间
振铃现象的持续时间受用于描述信号的频率成分数量的控制，而幅值受使用的滤波器的类型影响。接下来将使用具有无穷频率成分的方波来说明吉布斯现象。
振铃的持续时间：谐波截断
方波信号包含奇数的谐波成分，如图12所示。如果移除一些谐波（如截断），那么，方波的时域描述将不精确。
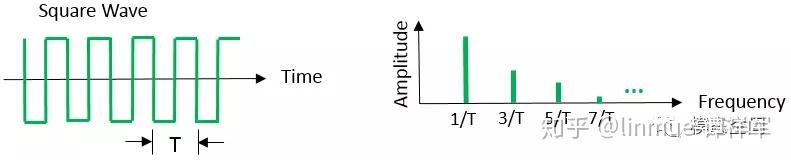图12 方波是一个具有无穷奇数谐波的信号
移除这些谐波，将引入吉布斯现象。在方波波形的转折处将产生振铃效应。在图13中，显示了同一个方波不同的情况：具有所有的谐波（蓝色）、谐波截断到2000Hz（红色）和谐波截断到750Hz（绿色），这是通过使用低通滤波器实现的。图13顶部显示同一方波的不同频谱：原始方波（蓝色）、低通2000Hz（红色）和低通750Hz（绿色）；底部显示与顶部相对应的时域波形。图13的下部分的时域信号表明，移除的谐波成分越多，振铃效应的持续时间越长。另外，包含的谐波成分越少，方波的阶跃或不连续过渡越平滑。在图13中，绿色曲线的斜率不如蓝色和红色陡峭。
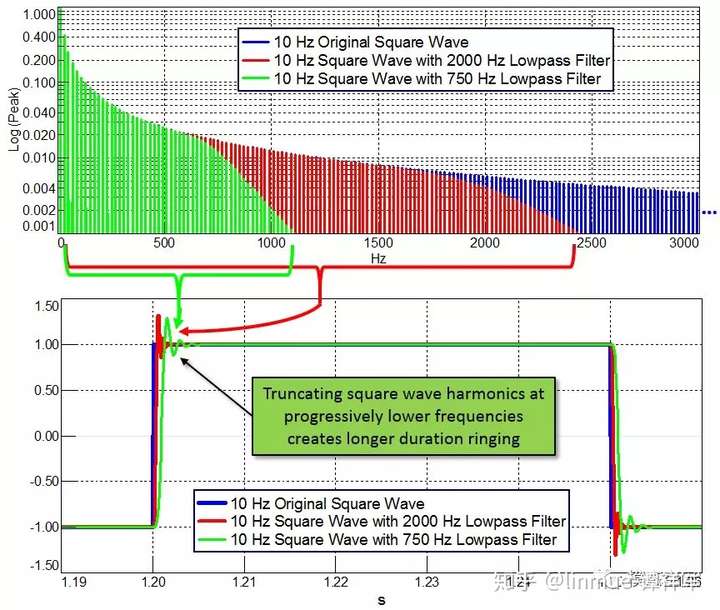图13 不同频率成分的方波的频谱（上）和时域波形（下）
测量信号过程中在决定是否出现吉布斯现象起到了重要的作用。如果信号不出现频率截断，那么，吉布斯现象将不会出现。例如，对一个单频正弦波施加低通滤波，那么，将不会出现振铃效应，如图14所示。对这个正弦波应用与图13相同频率设置的低通滤波，由于信号频率远低于低通滤波的截止频率，将不会影响单频正弦波，因为没有频率截断，从而不会出现吉布斯现象。因此，信号的类型也会影响吉布斯现象的出现。
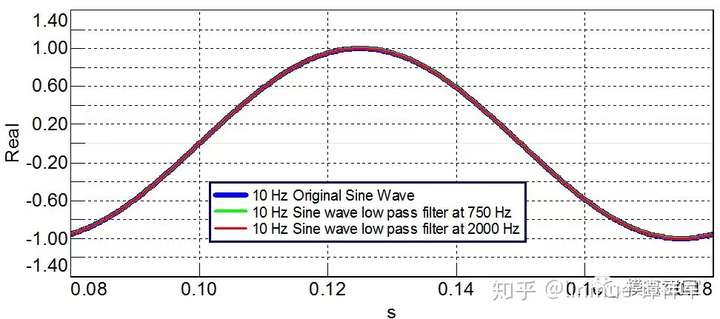图14 对正弦波设置不同的低通滤波频率，不出现吉布斯现象
当吉布斯效应出现时，振铃的幅值也部分受采集过程中的抗混叠低通滤波器形状的影响。
振铃的幅值：滤波器形状
信号测量经常使用抗混叠滤波器，这个低通抗混叠滤波器的形状对决定吉布斯现象中的振铃效应的幅值来说，是非常重要的。滤波器的锐度越大，振铃的幅值越大。
图15中重叠显示了两种不同类型的滤波器：一种是贝塞尔滤波器，一种是巴特沃斯滤波器。相比巴特沃斯滤波器，贝塞尔滤波器衰减更平坦，锐度更小。贝塞尔滤波器和巴特沃斯滤波器有相同的-3dB截止点（是它们的交点），但贝塞尔滤波器衰减更平坦。
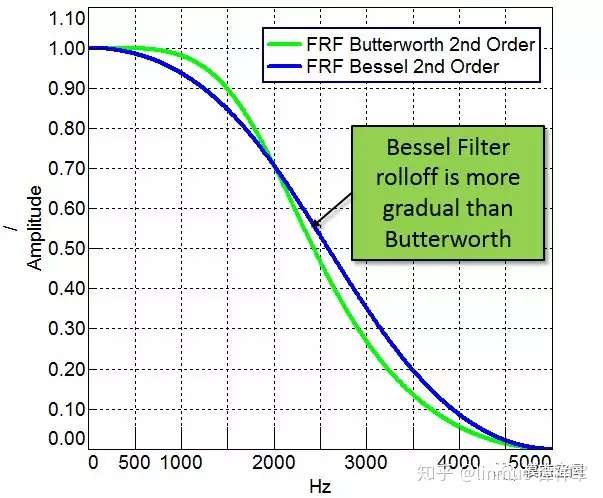图15 对比2阶，低通截止2000Hz的贝塞尔滤波器与巴特沃斯滤波器
在图16中，贝塞尔滤波后的方波的振铃效应的幅值低于相同的方波经巴特沃斯滤波后的振铃幅值。实际上，设计的巴特沃斯滤波器具有固定的过冲。从图16中可以看出，更平坦的贝塞尔滤波不会引入时域的振铃效应，不像更锐的巴特沃斯滤波。
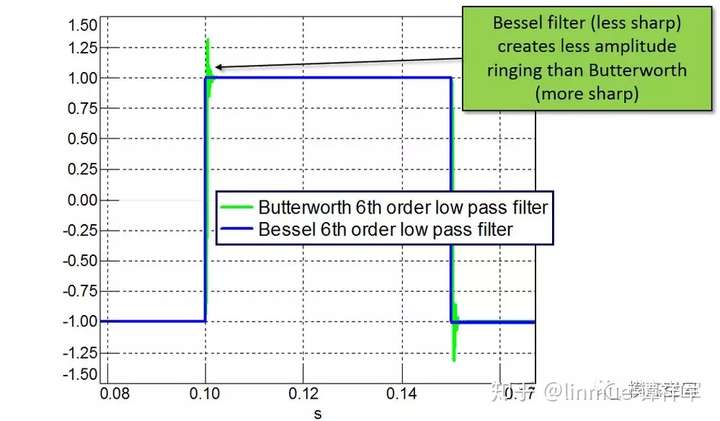图16 经贝塞尔滤波器与巴特沃斯滤波器低通截断后的方波
滤波器的形状越尖锐，时域数据出现吉布斯现象的可能性更大。为什么会这样呢？本质上，它与滤波器的时域形状相关。
当对频域的滤波器形状进行傅里叶逆变换时，结果称之为“脉冲”或“时间阶跃函数”。滤波器的频域带宽越宽，时域脉冲持续时间越短。随着脉冲持续时间的变短，振铃现象越占主导。这就是为什么更陡峭的巴特沃斯滤波产生了振铃，而更平坦的贝塞尔滤波器却没有。
4 吉布斯现象实例
在文章的起始部分，我们讲到转速测量时，方波信号会出现吉布斯现象。通过上面的分析，想必你已经清楚原因：方波具有无穷的频率成分，但由于采样时只能按一定的采样率进行，因此，必将出现频率截断，从而导致出现吉布斯现象。
另外，我们还讲到锤击法测试时的力脉冲有时也会出现振铃现象，这也是吉布斯现象。在文章《05.08：为什么力脉冲会出现振铃现象？》中，我们讲到设置不同的频率带宽对观测到的振铃效应的影响。使用四种不同硬度的锤头，设置两组不同的频率范围。四种锤头分别为非常软的红色气囊锤头、中等硬度的蓝色塑料锤头、较硬的白色塑料锤头和金属锤头。每种情况下，锤头锤击结构便获得一条时域力脉冲波形。在一组测试中，设置频率带宽为400Hz，另一组测试中，设置频率带宽为1600Hz。图17和图18中显示了这两组不同带宽、不同锤头锤击得到的力脉冲时域波形。两图从顶部到底部，分别对应的锤头由最软到最硬。
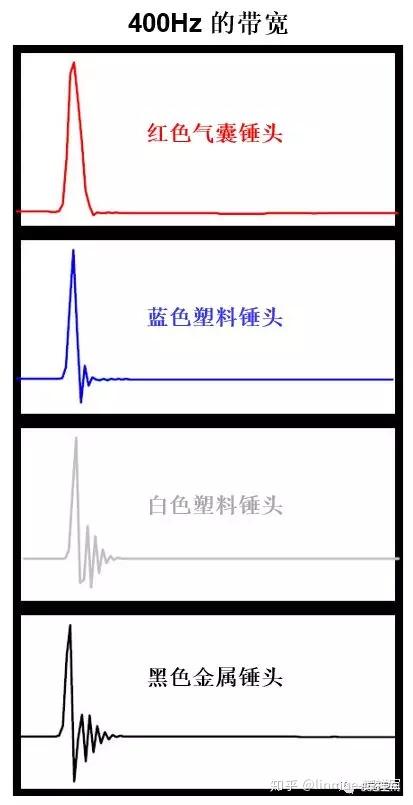图17 锤击设置400Hz的带宽
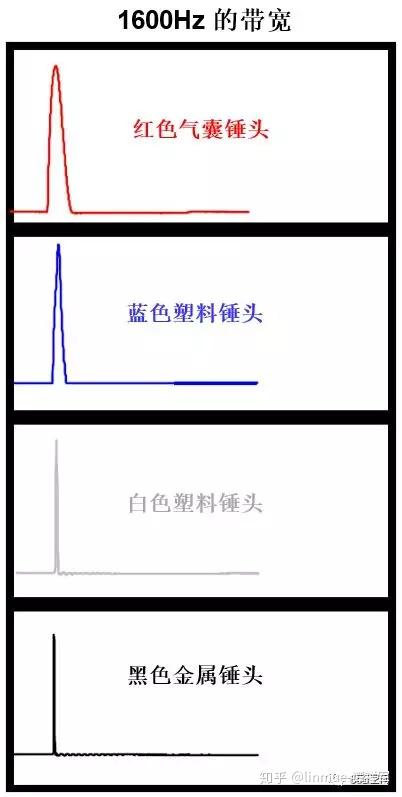图18 锤击设置1600Hz的带宽
注意到400Hz带宽内，随着锤头由软到硬，力脉冲振铃现象越来越明显。比较400Hz和1600Hz的带宽，力脉冲振铃效应有明显的变化：1600Hz带宽几乎没有明显振铃现象：前面两个锤头根本看不出振铃现象，后面两个锤头有很轻微的振铃现象。二者唯一不同之处是选择的带宽不同。
这是因为越硬的锤头，力脉冲作用时间越短，越能激起更宽的频率范围，或者说描述更短的力脉冲，需要更多数目的频率成分。随着锤头由软到硬，能激起的频率范围越来越宽，那么，400Hz以上的频率成分越来越多，当带宽设置为400Hz时，移除的频率成分会越来越多，即频率截断越严重，原理同图13，这样导致振铃效应越来越明显。而当带宽设置为1600Hz时，这个带宽内的频率成分用来描述前面两个软锤头的力脉冲是合适的，因此，不会出现吉布斯现象。但当采用白色塑料头和金属头时，力脉冲的作用时间更短，能激起更宽的频率范围，这在一定程度上超出了1600Hz，因而造成了频率截断，故，这两个锤头也出现了很轻微的振铃现象。
5 结论
采样过程中，由于数据采集系统只能采集到一定频率范围之内的信号，如果信号的频率成分没有越出数据采集设备采样时的带宽，那么将不会出现吉布斯现象；如果信号的频率成分超出了数据采集设备采样时的带宽，那么，将会出现吉布斯现象。但是可通过使用合适的抗混叠低通滤波器，吉布斯现象对测量的时域信号的影响可以很大程度上减小或消除。以下方法应时刻记住：
- 可通过在数据采集过程中使用合适的抗混叠低通滤波器避免产生不可预测的过冲的振铃效应的吉布斯现象。滤波器的频率截断和形状影响着吉布斯现象的幅值和持续时间。
- 在包含阶跃或不连续的瞬态信号中，也可观察到吉布斯现象。正弦信号不会出现吉布斯现象。在数据采集过程中，只有当移除了信号的部分频率成分时，才会出现吉布斯现象。
- 吉布斯现象主要影响时域，不影响频域。
参考：
- 维基百科；
- 部分图文来自内部文档；
- Peter Avitabile 《Modal Space》
-------转载知乎。-------