#include<bits/stdc++.h> #define int long long using namespace std; const int N=10005,mod=340610; int a[N],ans=1,n; signed main() { scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); for(int i=1;i<=n;i++) if(a[i]==a[i-1]) continue; else if(a[i]-a[i-1]==1) ans=(ans%mod*(2*i-1-2*a[i-1])%mod)%mod; else if(a[i]-a[i-1]==2) ans=(ans%mod*(i-1-a[i-1])*(i-1-a[i-1])%mod)%mod; else { ans=0; break; } printf("%lld",ans); return 0; }
http://noip.ybtoj.com.cn/contest/9/problem/4
这道题看了题解才做出来。。。。
我们把一个排列看成一个二维矩阵g,行坐标表示这个排列中数的下标,列坐标表示第几个数,g[i][j]==1就表示这个排列中的第i个数是j。
(接下来抄题解)
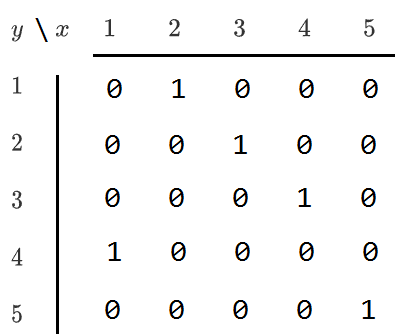
对于排列23415我们可以得到上图的矩阵。
满足a数组的排列需要满足的条件就是 在1~i个数中,小于等于i的数正好有a[i]个,对应到矩阵中,即 以(1,1)为左上角,以(i,i)为右下角的矩阵中,正好有a[i]个1。
然后我们考虑从内向外来填这个矩阵(有后效性,所以要从里往外) 显然,每一行,每一列都只能有1个1.(可以解释前面的选择对后面选择数量的影响)
然后就是方案的计算:
 最后, 当n=1时是不用特判的。
最后, 当n=1时是不用特判的。