week 5: ;Lasso regression & coordinate descent

笔记。

岭回归, 计算回归系数时使（ RSS(w)+λ||w||²) 最小

　　岭回归的结果会是所有的特征的weight都较小，但大多数又不完全为零。

　　而实际情况中，有的特征的确与输出值相关程度很高，weight本就应该取一个较大的值，

而有的特征与输出结果几乎毫无关系，取一个很小的值不如直接取零。

　　岭回归的结果，一方面使“非常有用的”特征权值取不到一个较大的值，"有用"的特征无法很好表达，

另一方面又不能有效的筛掉“无用”的特征，很累赘。在特征很少时，这个缺陷可能没什么影响，但当

特征很多时，岭回归的缺陷较为明显。后续计算复杂度显著提高（很多非零的weight实际上很小）。

　　一个解决方法是在合理的范围里提高结果 （weights）的稀疏度（sparsity），尽量只留下“有用”的

特征的权值，其他相关度低的特征权值直接取零。这样后续计算只需要关注非零的权值,复杂度大大降低。

如何筛选出部分”有用“的特征？

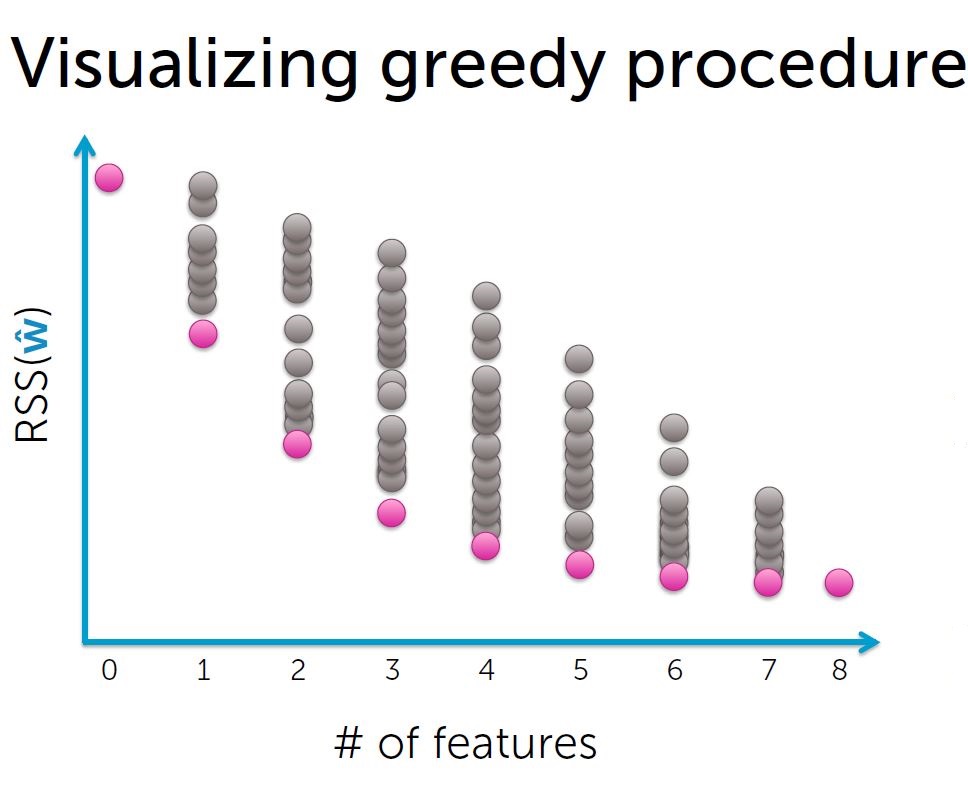
一个方法是使用贪婪算法。

过程：

　　1. 特征集合F初始为空集；

　　2.用特征集合F拟合模型，得到weights, 计算training error;

　　3.选择下一个最佳特征 f:

　　　使用{F+f}作为特征集合可以使training error达到新低；

　　4. F <-- F+ f

　　5.递归

　　　

　　

Lasso 回归： minimize （RSS(w)+λ||w||₁）

||w||₁为L1 范数，系数绝对值之和 |w|

|w|导数？

直接解方程 或 梯度下降 方法都不适用。

可以用subgradient 方法。

Coordinate descent:

用于解决一类最小值问题。适用于 直接求全局最小值很困难， 但单个坐标求最小值很容易 的函数。

求解过程：

　　　　

　　1. 初始化

　　2. 循环，单个坐标一个个更新到最小值

　　3. 计算每一步的步长（步长应越来越小），当最大步长 < ε 停止，否则循环

　　　　

　　　　　　

def lasso_coordinate_descent_step(i, feature_matrix, output, weights, l1_penalty):
    # compute prediction
    prediction = predict_output(feature_matrix, weights)
    # compute ro[i] = SUM[ [feature_i]*(output - prediction + weight[i]*[feature_i]) ]
    ro_i = np.dot(feature_matrix[:,i],(output - prediction + weights[i]*feature_matrix[:,i]))
    
    if i == 0: # intercept -- do not regularize
        new_weight_i = ro_i 
    elif ro_i < -l1_penalty/2.:
        weight_i = ro_i + l1_penalty/2.
    elif ro_i > l1_penalty/2.:
        new_weight_i = ro_i - l1_penalty/2.
    else:
        new_weight_i = 0.
    
    return new_weight_i



def lasso_cyclical_coordinate_descent(feature_matrix, output, weights, l1_penalty, tolerance):
    
    converged = False
    
    while converged == False:
        coordinate = []
        for i in xrange(len(weights)):
            old_weights_i = weights[i] # remember old value of weight[i], as it will be overwritten
            # the following line uses new values for weight[0], weight[1], ..., weight[i-1]
            #     and old values for weight[i], ..., weight[d-1]
            weights[i] = lasso_coordinate_descent_step(i, feature_matrix, output, weights, l1_penalty)

            # use old_weights_i to compute change in coordinate
            coordinate.append(abs(weights[i] - old_weights_i))
            if max(coordinate) < tolerance:
                converged = True
                
    return weights