华盛顿大学 机器学习 笔记。
k-means的局限性
k-means 是一种硬分类（hard assignment）方法，例如对于文档分类问题，k-means会精确地指定某一文档归类到某一个主题，但很多时候硬分类并不能完全描述这个文档的性质，这个文档的主题是混合的，这时候需要软分类（soft assignment）模型。
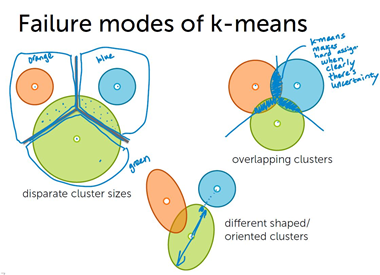
k-means 缺陷：（1）只关注聚类中心的表现。（2）聚类区域形状必须为对称圆形／球形，轴平行。
对于聚类区域大小不一、轴不平行、聚类空间重叠等情况，k-means 缺陷显著。
混合模型的优点：
1.软分类（例如，主题 54%“世界新闻”，45% “科学”， 1% “体育”）
2.关注聚类区域形状而不只是中心
3.每个聚类的权重（weights）可学习
高斯混合模型(GMM)
(1) 高斯函数描述聚类分布
高斯混合模型假定每个聚类可以用一个高斯分布函数N(x|μ ,Σ)描述，如图
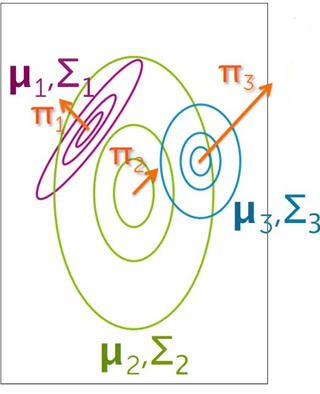
描述聚类的参数有三个， { π, μ , Σ }，其中，π 为聚类 的权重（weight），μ为 聚类的平均值（mean），Σ 为聚类的协方差（covariance）.
高斯混合模型概率分布:
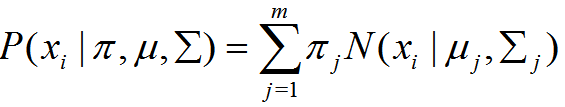
如何理这个解概率分布模型，以计算点xi属于聚类k的概率为例。
（2）如何计算点 xi 属于聚类k 的概率？
贝叶斯公式：
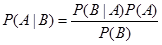
假设从数据集中随机抽取一个数据点，考虑以下几种情况：
A = 抽到的点属于聚类k
B = 抽到点xi
B|A = 已知抽取的点属于聚类k 中, 抽到点xi
A|B = 已知抽到点xi, 抽取的点属于聚类k
P(A|B)其实等价于”点xi属于聚类k”的概率。
接下来求P(A)、P(B)、P(B|A)，通过贝叶斯公式可求P(A|B)。
A = 抽到的点属于聚类k
P(A)：从数据集中随机抽取一个点，恰好抽到聚类k中的点的概率。
（其中，所有聚类权重之和为1，即 
，m为聚类数量)
即
B|A = 已知抽取的点属于聚类k,中, 抽到点xi
P(B|A)：转换为从聚类k中随机抽一个点，恰好抽到点xi的概率。
GMM模型假设每个聚类中数据点服从高斯分布：
即
B = 抽到点xi
P(B)：从数据集中随机抽取一个点，恰好抽到点xi的概率。
这种情况下，抽到的点归属于哪个/些聚类未知，考虑到：
如果已知抽到的点属于哪些聚类，这个概率可以按照P(B|A)的公式算。
从数据集中随机抽点，抽到的点属于某个聚类的概率，可以按照P(A)的公式计算。
使用用条件概率公式计算：
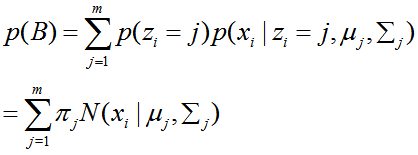
这就是就是GMM模型的概率分布模型。
点xi属于聚类k的概率，即后验概率为：
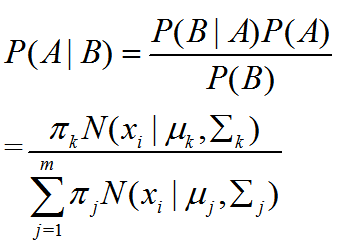
即
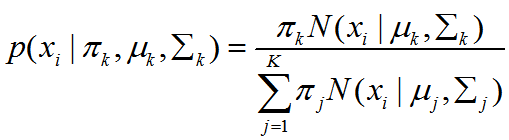
（3）评估GMM模型优劣的方法——似然性
首先明确隐变量：
假设整个数据集是从符合这个GMM模型的大样本中随机抽取点构成的，每次抽取的数据记为 xi（i = 1,2,…,N， 数据集中一共N个点）,对于第i次抽取的点，此时xi是已知的，而 xi属于哪个聚类未知，以隐变量γ表示，其中
γ为随机变量。则变量的完全数据为
似然函数表示的是，在当前GMM模型的参数下，以上述方法形成的数据集，恰好构成了原本的数据集的概率。
似然函数计算式：
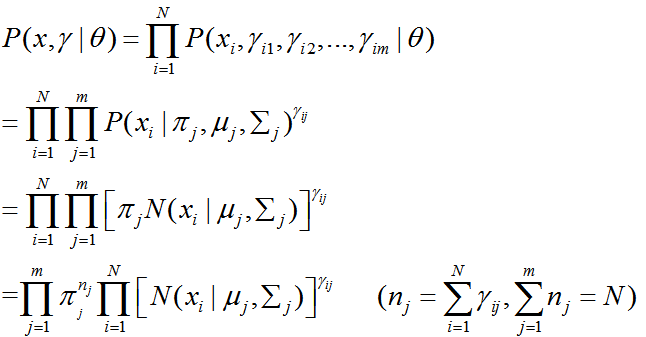
其中多维高斯分布函数（维数为dim）：
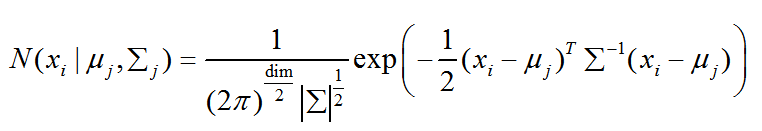
实际应用中常常使用对数似然函数：
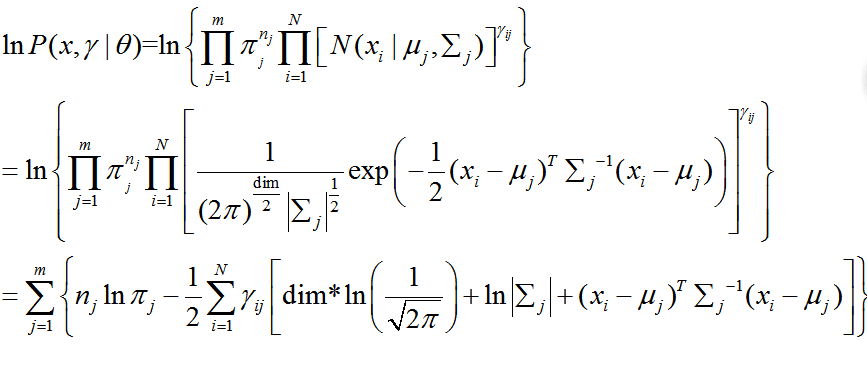
EM算法
EM算法（expectation maximization, 期望最大化），计算GMM模型分两步：
1. E- step： 根据当前GMM模型的参数，计算（estimate）对数似然性的期望值。
2. M-step： 求使似然性(likelihood)期望最大的新的模型参数。
E-step：
对数似然性表达式：
求期望要先明确一件事，随机变量是什么？
隐变量γ
即
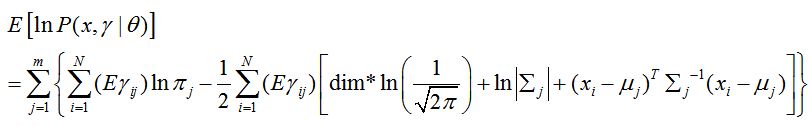
隐变量
的期望称为聚类k对xi的响应度（responsibility）。记为
考虑到表示的意义是，xi是否属于聚类k。因此的期望就是在当前模型参数下，xi属于聚类k的概率，即
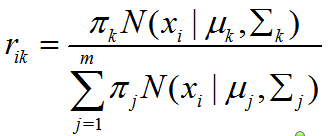
带入原式得：
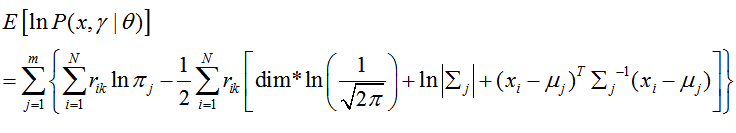
def log_sum_exp(Z):
""" Compute log(sum_i exp(Z_i)) for some array Z."""
return np.max(Z) + np.log(np.sum(np.exp(Z - np.max(Z))))
def loglikelihood(data, weights, means, covs):
""" Compute the loglikelihood of the data for a Gaussian mixture model. """
num_clusters = len(means)
num_dim = len(data[0])
num_data = len(data)
resp = compute_responsibilities(data, weights, means, covs)
log_likelihood = 0
for k in range(num_clusters):
Z = np.zeros(num_clusters)
for i in range(num_data):
# Compute (x-mu)^T * Sigma^{-1} * (x-mu)
delta = np.array(data[i]) - means[k]
exponent_term = np.dot(delta.T, np.dot(np.linalg.inv(covs[k]), delta))
Z[k] += np.log(weights[k])
Z[k] -= 1/2. * (num_dim * np.log(2*np.pi) + np.log(np.linalg.det(covs[k])) + exponent_term)
Z[k] = resp[i][k]* Z[k]
log_likelihood += log_sum_exp(Z)
return log_likelihood
M-step:
求使似然性期望最大的新的模型参数。似然性期望的公式：
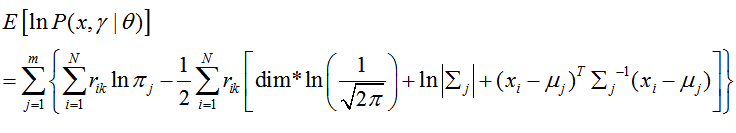
用这个式子分别对 { π, μ , Σ }这几个参数求偏导数，并令偏导数为0，即可得到新的模型参数。
聚类k的新参数计算：
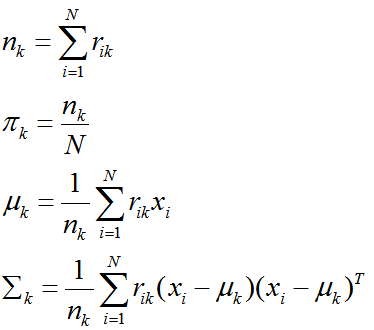
EM是一种 坐标上升(coordinate-ascent)算法，多次迭代直到对数似然函数的值不再有明显变化，得到局部最优解。
def EM(data, init_means, init_covariances, init_weights, maxiter=1000, thresh=1e-4):
# Initialize
means = init_means[:]
covariances = init_covariances[:]
weights = init_weights[:]
num_data = len(data)
num_dim = len(data[0])
num_clusters = len(means)
resp = np.zeros((num_data, num_clusters))
log_likelihood = loglikelihood(data, weights, means, covariances)
ll_trace = [log_likelihood]
for it in range(maxiter):
# E-step:
resp = compute_responsibilities(data, weights, means, covariances)
# M-step:
# 更新 n(k),weight(k),mean(k),covariances(k)
counts = compute_counts(resp)
weights = compute_weights(counts)
means = compute_means(data, resp, counts)
covariances = compute_covariances(data, resp, counts, means)
# 计算此次迭代之后的log likelihood
ll_latest = loglikelihood(data, weights, means, covariances)
ll_trace.append(ll_latest)
# 收敛？
if (ll_latest - log_likelihood) < thresh and ll_latest > -np.inf:
break
log_likelihood = ll_latest
model = {'weights': weights, 'means': means, 'covs': covariances, 'loglik': ll_trace, 'resp': resp}
return model