一、概述
1.状态压缩
状态压缩就是使用某种方法,简明扼要地以最小代价来表示某种状态,通常是用一串01数字(二进制数)来表示各个点的状态。这就要求使用状态压缩的对象的点的状态必须只有两种,0 或 1;当然如果有三种状态用三进制来表示也未尝不可。
2.使用条件
从状态压缩的特点来看,这个算法适用的题目符合以下的条件:
解法需要保存一定的状态数据(表示一种状态的一个数据值),每个状态数据通常情况下是可以通过2进制来表示的。这就要求状态数据的每个单元只有两种状态,比如说棋盘上的格子,放棋子或者不放,或者是硬币的正反两面。这样用0或者1来表示状态数据的每个单元,而整个状态数据就是一个一串0和1组成的二进制数。
解法需要将状态数据实现为一个基本数据类型,比如int,long等等,即所谓的状态压缩。状态压缩的目的一方面是缩小了数据存储的空间,另一方面是在状态对比和状态整体处理时能够提高效率。这样就要求状态数据中的单元个数不能太大,比如用int来表示一个状态的时候,状态的单元个数不能超过32(32位的机器),所以题目一般都是至少有一维的数据范围很小。
3.状压DP
状压DP,顾名思义,就是使用状态压缩的动态规划。
动态规划问题通常有两种,一种是对递归问题的记忆化求解,另一种是把大问题看作是多阶段的决策求解。这里用的便是后一种,这带来一个需求,即存储之前的状态,再由状态及状态对应的值推演出状态转移方程最终得到最优解。
二、位运算
一般基础的状压就是将一行的状态压成一个数,这个数的二进制形式反映了这一行的情况。由于使用二进制数来保存被压缩的状态,所以要用到神奇的二进制位运算操作,将一个十进制数转成二进制进行位运算操作再转回十进制数。
| 名称 | 运算符 | Pascal样式 | 简记法则 |
|---|---|---|---|
| 按位与 | & | and | 全一为一,否则为零 |
| 按位或 | | | or | 有一位一,否则为零 |
| 按位取反 | ~ | not | 是零则一,是一则零 |
| 按位异或 | ^ | xor | 不同则一,相同则零 |
| 左移位 | << | shl | a<<k等价于a*2^k |
| 右移位 | >> | shr | a>>k等价于a/2^k |
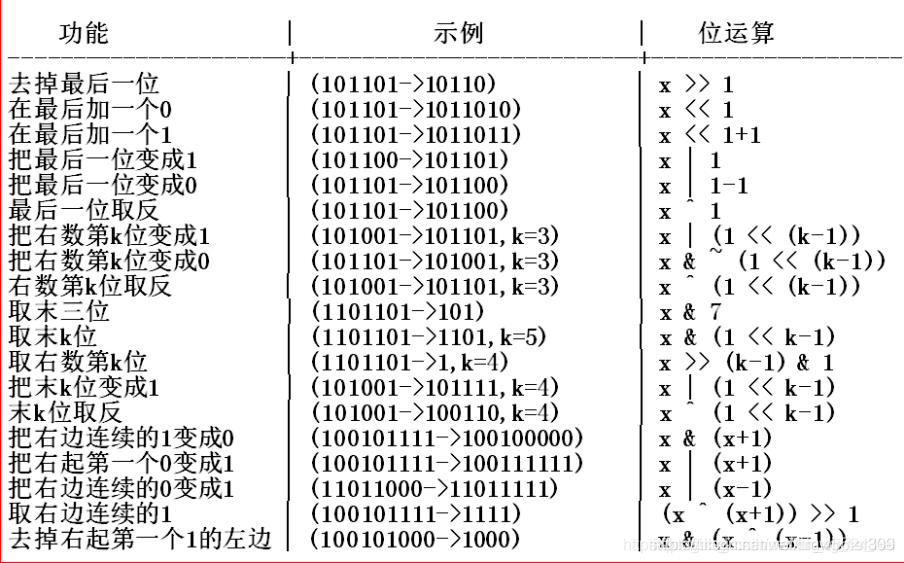
注:在涉及到位运算时,一定要注意位运算的优先级。该加的括号一定要加
定义状态(例如) 求每一种放法的背包价值,状态应该是这n件物品的放与不放的情况。
最容易想到的是开个n维数组,第i个维度的下标如果是1的话代表放第i件物品,0的话代表不放第i件物品;
但是这样很容易造成空间浪费,而且多维数组也不好开;
我们仔细观察就会发现,每件物品有放与不放两种选择;假设我们有5件物品的时候,用1和0代表放和不放
如果这5件物品都不放的话,那就是00000;
如果这5件物品都放的话, 那就是11111;
看到这,我们知道可以用二进制表示所有物品的放与不放的情况;如果这些二进制用十进制表示的话就只有一个维度了。而且这一个维度能表示所有物品放与不放的情况;这个过程就叫做状态压缩;
注:先简单写一下 回头再改一下