1、原始损失函数
- 由最小二乘法得到的损失函数为
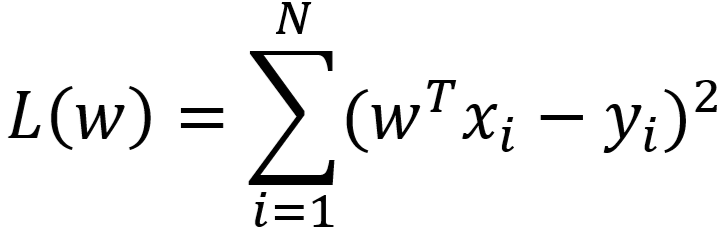
- 最小二乘法得到的参数 w 的极大似然估计值为
![]()
- 由于
 有可能是不可逆矩阵,因此
有可能是不可逆矩阵,因此  可能无法得到解析解(即方程有无数多个解,易造成过拟合)
可能无法得到解析解(即方程有无数多个解,易造成过拟合)
2、正则化框架

- L(w) 为最小二乘法得到的损失函数(Loss)
- P(w) 可理解为罚函数
- 常用 L1/L2 范数作为罚函数
- L1 范数:
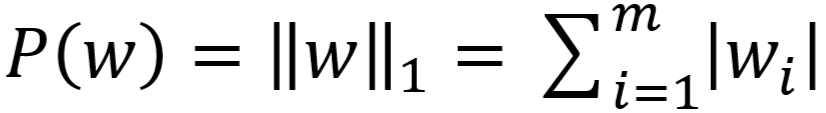
- L2 范数:
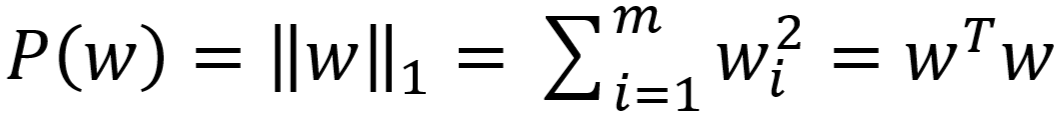
- 使用 L1 范数的正则化称作 L1正则化(Lasso回归,又叫套索回归)
- 使用 L2 范数的正则化称作 L2 正则化(Ridge 回归,又叫岭回归)
- L1 范数:
- 常用 L1/L2 范数作为罚函数
- λ 为正则化参数
- λP(w) 为正则项
3、L2 正则化原理推导
- 对于 L2 正则化,损失函数为
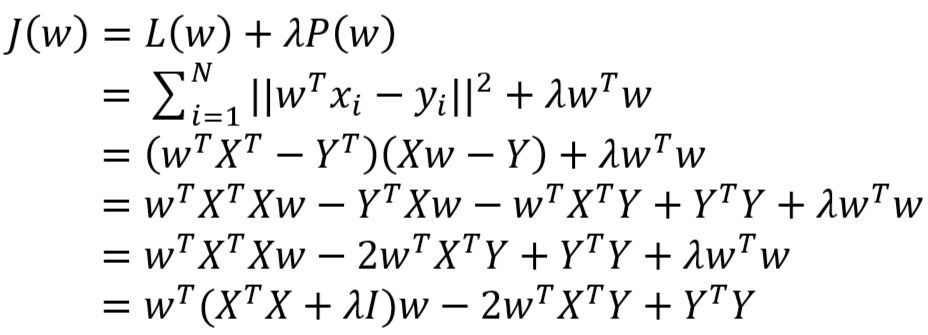
- 得到的参数 w 的极大似然估计值为:
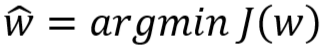
-
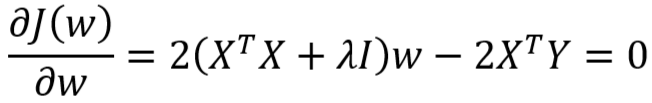
- 由上式得:
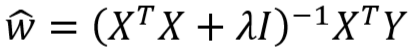
- L2 正则化的意义
- 由上推导可知,正则化前后 w 估计值如下:
- 正则化前:
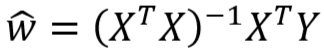
- L2 正则化后:
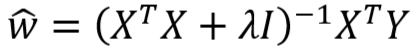
- 正则化前:
- 由 1 可知,
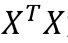 为半正定矩阵,有可能是不可逆矩阵,因此
为半正定矩阵,有可能是不可逆矩阵,因此  可能无法得到解析解
可能无法得到解析解
- 由上推导可知,正则化前后 w 估计值如下:
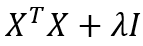 ,半正定矩阵
,半正定矩阵  加上一个对角矩阵 λI,得到的是一个正定矩阵,因此
加上一个对角矩阵 λI,得到的是一个正定矩阵,因此 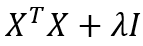 一定可逆,
一定可逆, 可以得到解析解
可以得到解析解- 综上可知,L2 正则化解决了
 可能无解析解的缺陷,因此避免了过拟合
可能无解析解的缺陷,因此避免了过拟合