zoukankan html css js c++ java

JAVA基于权重的抽奖

https://blog.csdn.net/huyuyang6688/article/details/50480687

如有4个元素A、B、C、D，权重分别为1、2、3、4，随机结果中A:B:C:D的比例要为1:2:3:4。

总体思路：累加每个元素的权重A(1)-B(3)-C(6)-D(10)，则4个元素的的权重管辖区间分别为[0,1)、[1,3)、[3,6)、[6,10)。
然后随机出一个[0,10)之间的随机数。落在哪个区间，则该区间之后的元素即为按权重命中的元素。

实现方法：
利用TreeMap，则构造出的一个树为:
B(3)
　　　 /
/
A(1) D(10)
/
/
C(6)

然后，利用treemap.tailMap().firstKey()即可找到目标元素。

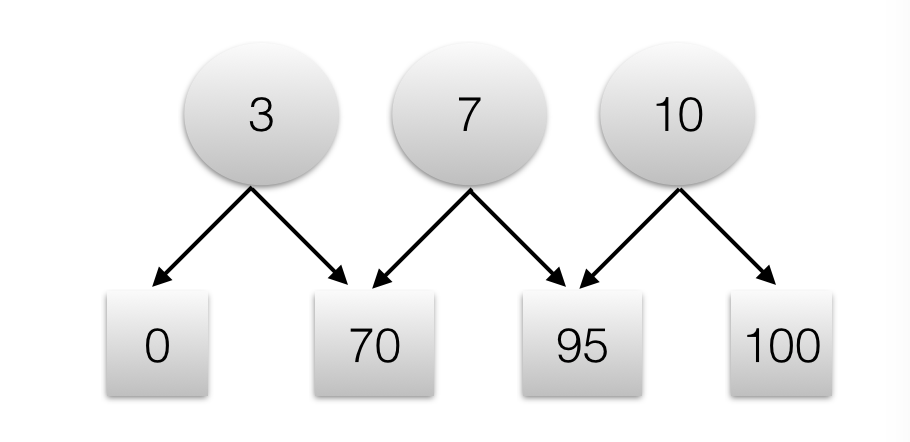(3落在70%权重，7落在70-95的权重，10落在95-100的权重)

https://www.bbsmax.com/A/LPdo4pk2z3/

三、依赖不可控的物理随机数

什么意思呢，先看个图，看完你就知道了

明白了吧，呵呵，这就是现如今灰常流行的一种抽奖算法，绝对公平、绝对透明、绝对木有暗箱（除非偷偷给你换了抽奖号码）！但是这种方法唯一的缺点是无法实时抽奖，只能事后抽奖。也就是只能拿个抽奖号等着上帝的眷顾，阿门。。。

例如游戏中打败一个boss，会掉落下面其中一个物品，而每个物品都有一定概率： 1. 靴子 20% 2. 披风 25% 3. 饰品 10% 4. 双手剑 5% 5. 金币袋 40% 现在的问题就是如何根据概率掉落一个物品给玩家。

一. 一般算法：生成一个列表，分成几个区间，例如列表长度100，1-20是靴子的区间，21-45是披风的区间等，然后随机从100取出一个数，看落在哪个区间。算法时间复杂度：预处理O(MN)，随机数生成O(1)，空间复杂度O(MN)，其中N代表物品种类，M则由最低概率决定。

二、离散算法：也就是上面的改进，竟然1-20都是靴子，21-45都是披风，那抽象成小于等于20的是靴子，大于20且小于等于45是披风，就变成几个点[20,45,55,60,100]，然后也是从1到99随机取一个数R，按顺序在这些点进行比较，知道找到第一个比R大的数的下标，比一般算法减少占用空间，还可以采用二分法找出R，这样，预处理O(N)，随机数生成O(logN)，空间复杂度O(N)。请点击查看详细：http://www.cnblogs.com/miloyip/archive/2010/04/21/1717109.html

三、Alias Method Alias Method就不太好理解，实现很巧妙，推荐先看看这篇文章：http://www.keithschwarz.com/darts-dice-coins/ 大致意思：把N种可能性拼装成一个方形（整体），分成N列，每列高度为1且最多两种可能性，可能性抽象为某种颜色，即每列最多有两种颜色，且第n列中必有第n种可能性，这里将第n种可能性称为原色。想象抛出一个硬币，会落在其中一列，并且是落在列上的一种颜色。这样就得到两个数组：一个记录落在原色的概率是多少，记为Prob数组，另一个记录列上非原色的颜色名称，记为Alias数组，若该列只有原色则记为null。

之前的例子，为了便于演示换成分数 1. 靴子 20% -> 1/4 2. 披风 25% -> 1/5 3. 饰品 10% -> 1/10 4. 双手剑 5% -> 1/20 5. 金币袋 40% -> 2/5 然后每个都乘以5（使每列高度为1），再拼凑成方形拼凑原则：每次都从大于等于1的方块分出一小块，与小于1的方块合成高度为1

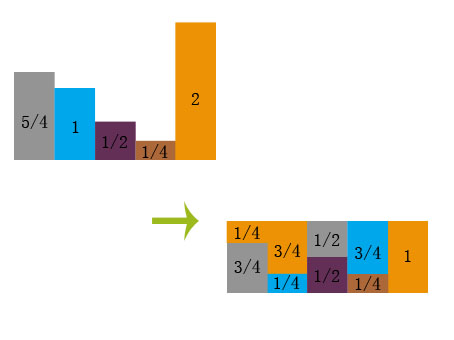
由上图方形可得到两个数组： Prob: [3/4, 1/4, 1/2, 1/4, 1] Alias: [4, 4, 0, 1, null] (记录非原色的下标)

之后就根据Prob和Alias获取其中一个物品随机产生一列C，再随机产生一个数R，通过与Prob[C]比较，R较大则返回C，反之返回Alias[C]。

Alias Method 复杂度：预处理O(NlogN)，随机数生成O(1)，空间复杂度O(2N)

https://www.cnblogs.com/younggun/p/3249772.html

简介

最近闲的无聊，将以前做的一个微信抽奖小demo拿来分享一下,以便加深印象。

效果图

1.gif

业务要求

在一个奖池中放一堆奖品，分别给它们设置不同的数量,比如一等奖A10个，二等奖B，30个，三等奖C10个，然后设置参与人数C人
条件是：
当奖品数大于参与人数，100%中奖。
当奖品A发放完是，不能被抽中。
当奖品发放完毕是，该抽奖活动自动下架。
同一个用户如果中奖了，将不能继续参与该活动。
这里只讨论下其中的核心算法的设计及一个示例函数，算法之外的系统控制暂不提及。
实现抽奖的方法应该有很多，没有仔细去考察和搜索那些非常复杂的算法，这里仅做了一个简单的假设，并在此基础上推出后面所有的控制逻辑。

实现方法

java核心抽奖代码如下:

public class LotteryUtil {
    /**
     * 
     * @param orignalRates  传人每一个奖品概率的集合,(集合的第一个参数是0.0 表示百分比中奖)
     * @return
     */
    public static int lottery(List<Double> orignalRates) {
        if (orignalRates == null || orignalRates.isEmpty()) {
            return -1;
        }
        int size = orignalRates.size();
        // 计算总概率，这样可以保证不一定总概率是1
        double sumRate = 0d;
        for (double rate : orignalRates) {
            sumRate += rate;
        }
        // 计算每个物品在总概率的基础下的概率情况
        List<Double> sortOrignalRates = new ArrayList<Double>(size);
        Double tempSumRate = 0d;
        /*遍历奖品概率的集合，计算每一个奖品的中间区间*/
        for (double rate : orignalRates) {
            tempSumRate += rate;
            sortOrignalRates.add(tempSumRate/sumRate);
        }
        // 根据区块值来获取抽取到的物品索引
        double nextDouble = Math.random();
        sortOrignalRates.add(nextDouble);
        Collections.sort(sortOrignalRates);
        return sortOrignalRates.indexOf(nextDouble);
    }
}

抽奖的业务逻辑代码如下

    /*awardItems获取奖品的一个集合*/
    if (activityUserDao.getCountByOpenId(Award.WHEEL_AWARD_TYPE, wid, open_id) <= 0) {
                                        /* awardItems获取奖品的一个集合 */
                                        List<Award> awardItems = awardDao.getByActivity(aw.getWheel_id(), Award.WHEEL_AWARD_TYPE);
                                        /* lotterys存放每一个奖品的中奖概率集合 */
                                        List<Double> lotterys = new ArrayList<Double>();
                                        /* 获取总的奖品数量 */
                                        int count = 0;
                                        for (Award a : awardItems) {
                                            count += a.getProvide_count();
                                        }
                                        if (aw.getPeople_count() <= count) {
                                            lotterys.add(0.0); // 100%中奖
                                        } else {
                                            /* 预计参与人数减去奖品数 除以参与人数 = 未中奖概率 */
                                            lotterys.add((double) (aw.getPeople_count() - count) / (double) aw.getPeople_count());
                                        }
                                        /* 遍历奖品集合，获取每一个奖品中奖概率 */
                                        for (Award a : awardItems) {
                                            if (a.getOver_count() > 0) {
                                                lotterys.add((double) a.getProvide_count() / (double) aw.getPeople_count());
                                            } else {
                                                lotterys.add(0.0);
                                            }
                                        }
                                        // 计算中奖概率
                                        int index = LotteryUtil.lottery(lotterys);
                                        if (index > 0) {// 中奖
                                            Award a = awardItems.get(index - 1);
                                            long key = Math.round(Math.random() * (999999 - 100000) + 100000); // 6位数中奖序列号
                                            // 修改商品剩余数量 + 记录序列号
                                            if (awardDao.doLowerOverCount(a.getAward_id()) > 0
                                                    && activityUserDao.doInsert(new ActivityUser(aw.getPublic_id(), Award.WHEEL_AWARD_TYPE, wid, a.getAward_id(), key + "", open_id)) > 0) {
                                                rb.setCode(index);
                                                rb.setData(key);
                                                rb.setMessage(a.getAward_name());
                                            } else {
                                                rb.setCode(0);
                                            }
                                        }
                                        // 抽奖记录
                                        activityRecordDao.doInsert(new ActivityRecord(open_id, Award.WHEEL_AWARD_TYPE, wid, request.getRemoteAddr()));

前端抽奖工具类

/**
 * 注意：本插件运用了rem屏幕适配方案，一律采用rem作为单位，若项目中不是采用这种方案的，此段代码不会影响功能使用，仅会影响控件样式
 */

(function(win, doc, $) {

    var defaultOpt = {

        rotateNum: 5, //转盘转动圈数
        body: "", //大转盘整体的选择符或zepto对象

        disabledHandler: function() {}, //禁止抽奖时回调

        clickCallback: function() {}, //点击抽奖按钮,再次回调中实现访问后台获取抽奖结果,拿到抽奖结果后显示抽奖画面

        KinerLotteryHandler: function(deg) {} //抽奖结束回调

    };

    function KinerLottery(opts) {

        this.opts = $.extend(true, {}, defaultOpt, opts);

        this.doing = false;

        this.init();

    }

    KinerLottery.prototype.setOpts = function(opts) {

        this.opts = $.extend(true, {}, defaultOpt, opts);

        this.init();

    };

    KinerLottery.prototype.init = function() {

        var self = this;

        this.defNum = this.opts.rotateNum * 360; //转盘需要转动的角度
        // console.log(this.defNum);

        // alert(this.defNum);

        //点击抽奖
        $('#box').on('click', ".KinerLotteryBtn", function() {
            if($(this).hasClass('start') && !self.doing) {
                self.opts.clickCallback.call(self);
            } else {

                var key = $(this).hasClass('no_start') ? "noStart" : $(this).hasClass('completed') ? "completed" : "illegal";

                self.opts.disabledHandler(key);

            }

        });

        $(this.opts.body).find('.KinerLotteryContent').get(0).addEventListener('webkitTransitionEnd', function() {

            self.doing = false;

            var deg = $(self.opts.body).attr('data-deg');

            if(self.opts.direction == 0) {
                $(self.opts.body).attr('data-deg', 360 - deg);
                $(self.opts.body).find('.KinerLotteryContent').css({
                    '-webkit-transition': 'none',
                    'transition': 'none',
                    '-webkit-transform': 'rotate(' + (deg) + 'deg)',
                    'transform': 'rotate(' + (deg) + 'deg)'
                });
                self.opts.KinerLotteryHandler(360 - deg);
            } else {
                $(self.opts.body).attr('data-deg', deg);
                $(self.opts.body).find('.KinerLotteryContent').css({
                    '-webkit-transition': 'none',
                    'transition': 'none',
                    '-webkit-transform': 'rotate(' + (-deg) + 'deg)',
                    'transform': 'rotate(' + (-deg) + 'deg)'
                });
                self.opts.KinerLotteryHandler(deg);
            }

        });

    };
    KinerLottery.prototype.goKinerLottery = function(_deg) {
        if(this.doing) {
            return;
        }
        var deg = _deg + this.defNum;
        var realDeg = this.opts.direction == 0 ? deg : -deg;
        this.doing = true;
        $(this.opts.body).find('.KinerLotteryBtn').addClass('doing');

        $(this.opts.body).find('.KinerLotteryContent').css({
            '-webkit-transition': 'all 5s',
            'transition': 'all 5s',
            '-webkit-transform': 'rotate(' + (realDeg) + 'deg)',
            'transform': 'rotate(' + (realDeg) + 'deg)'
        });
        $(this.opts.body).attr('data-deg', _deg);
    };
    win.KinerLottery = KinerLottery;
})(window, document, $);

前端js调用抽奖类

/**
 * @author wjb
 * @description 
 * @version 1.0.0 2017/2/11
 */
app.controller("wheelOneController", ['$scope', '$stateParams', '$neu_', 'awardService', '$filter', '$timeout', 'util.alert', 'cfg', 'wxService', function($scope, $stateParams, $neu_, awardService, $filter, $timeout, alert, cfg, wxService) {
    /*中奖开始时间*/
    $scope.wheelStatu = {
            start: true,
            noStart: false,
            completed: false
        }
        /*错误信息提示*/
    $scope.errorMsg = "";
    /*定义奖品数据变量*/
    $scope.awards = [];
    /*活动的id和活动的微信公众号ID*/
    var activity_id = $neu_.isEmpty($stateParams.activity_id) ? 1 : $stateParams.activity_id;
    var public_id = $neu_.isEmpty($stateParams.public_id) ? 1 : $stateParams.public_id;
    var open_id = $neu_.isEmpty($stateParams.open_id) ? cfg.openId : $stateParams.open_id;
    cfg.public_id = public_id;
    cfg.open_id = open_id;
    cfg.activity_id = activity_id;
    //alert(cfg.public_id+"=="+cfg.activity_id+"=="+cfg.open_id );
    /*获取活动信息*/
    wxService.setConfig();
    awardService.getWheelInfo(activity_id, public_id).then(function(res) {
        //console.dir(res)
        if(res.success) {
            $scope.wheelStatu.start = true;
        } else {
            if(res.code == 1 || res.code == 3) {
                $scope.wheelStatu.noStart = true;
            } else if(res.code == 2) {
                $scope.wheelStatu.completed = true;
            }
            $scope.errorMsg = res.msg;
        }
        $scope.wheelInfo = res.data;
    });
    awardService.getAwards(activity_id, public_id).then(function(res) {
        $scope.awards = res.data;
    });
    /*奖品预览*/
    var result = [];
    $scope.showPic = function(pic) {
            if(result.length == 0) {
                $neu_.each($scope.awards, function(item) {
                    result.push(cfg.resourcePath + item.img);
                });
            }
            wxService.previewImage(cfg.resourcePath + pic, result);
        }
        /*中奖结果集*/
    $scope.result = [];
    $scope.user = {
        user_name: '',
        phone: '',
        activity_id: activity_id,
        user_openid: open_id
    };
    /**
     * 提交中奖人信息
     */
    $scope.submit = function() {
            $(".actBody_close").click();
            $scope.isLoading = true;
            awardService.updateLotteryUser($scope.user).then(function(res) {
                    $scope.isLoading = false;
                    if(res.success) {
                        alert('您的中奖信息已备案，我们的客服人员稍后会联系您，如何领取奖品');
                    } else {
                        alert('提交失败');
                    }
                })
                //alert('哈哈上当了吧^_^_^_^')
        }
    $scope.load = function() {
        $timeout(function() {
            ActBounced();
            $("#layer").hide();
            new KinerLottery({
                rotateNum: 5, //转盘转动圈数
                body: "#box", //大转盘整体的选择符或zepto对象
                direction: 0, //0为顺时针转动,1为逆时针转动
                disabledHandler: function(key) {
                    switch(key) {
                        case "noStart":
                            $scope.$apply(function() {
                                alert($scope.errorMsg);

                            });
                            break;
                        case "completed":
                            $scope.$apply(function() {
                                alert($scope.errorMsg);
                            });
                            break;
                    }
                }, //禁止抽奖时回调
                clickCallback: function() {
                    var this_ = this;
                    //此处访问接口获取奖品
                    $scope.isLoading = true;
                    awardService.startAweel(activity_id, open_id).then(function(res) {
                        $scope.isLoading = false;
                        if(isDebug){
                            this_.goKinerLottery(0);
                        }else{
                            if(res.success) {
                            var index = cfg.isDebug ? Math.floor(Math.random() * 5) : res.code;
                            $scope.result = $filter('awardToAngle')(index, $scope.awards);
                            if(index == 0) {
                                this_.opts.disabledHandler("noStart");
                            } else {
                                this_.goKinerLottery($scope.result[1]);
                            }
                        } else {
                            alert(res.msg);
                        }
                        }
                    })
                }, //点击抽奖按钮,再次回调中实现访问后台获取抽奖结果,拿到抽奖结果后显示抽奖画面
                KinerLotteryHandler: function(deg) {
                    $("#smallActAdv").click();
                }
            });

        }, 500);
        /*分享授权的地址*/
        $timeout(function(){
        var share ={shareUrl:"weixin/oauth.html?isBase=true&type=6&a_id="+activity_id+"&p_id="+public_id+"&appid="+cfg.appId};
        wxService.onMenuShareAppMessage(share);
        },3000)
    }
}])

以上是抽奖的主要代码

作者：薪火设计
链接：https://www.jianshu.com/p/8e6c43f90faa
來源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。

一个简单抽奖算法的实现以及如何预防超中
需求

每个用户每天有3次抽奖机会；
抽奖奖池一共分为6档内容：现金红包1元，2元，3元，5元，iphone6s，谢谢参与；
支持每天调整和配置抽奖的获奖概率；

算法介绍
每种奖品都有一个权重对应一个区间若落入该区间就表示中奖调整区间大小就可改变获奖概率即调整权重值即可

奖品	权重	区间
1元	5000	[0,5000)
2元	1000	[5000,6000)
3元	500	[6000,6500)
5元	100	[6500, 6600)
iphone6s	1	[6600, 6601)
未中奖	59409	[6601,66010)	假设设定抽10次中一次, 未中奖权重 = 抽检概率导数奖品数-奖品数 = 106601-6601 = 59409

抽奖的时候先生成一个随机值

randNum = new Random().nextInt(totalWeight); // totalWeight = 上面权重列之和

判断该随机值在哪一个区间如

randNum = 8944 落在未中奖区间 未中奖 
randNum = 944 落在1元区间 中了一元

如果想增大中iphone6s的概率调整权重值即可如将权重改为1000，则区间变为[6600,7600)
同时会为每种奖品设置库存如

日期	奖品	库存
3.1	一元	5000

中奖后会减库存但假如库存只剩1个了有10个用户同时落入一元区间如何避免1-10=-9的情况呢？
解决方法

update award_stock set stock = stock - 1 where award_id = ? and stock > 0;

即是否中奖除了落入区间外还需判断减库存是否成功
如果减库存失败仍当做未中奖

一旦一种奖品库存为0 下次计算区间的时候将它排除如一元奖品库存已为0 这时各奖品的区间变化为

奖品	权重	区间
2元	1000	[0,1000)
3元	500	[1000,1500)
5元	100	[1500, 1600)
iphone6s	1	[1600, 1601)
未中奖	59409	[1601,61010)	61010/1601=38 此时中奖概率变小了相当于抽38次中一次

验证上述算法
看是否能抽完所有奖品如某天的奖品配置如下 (权重默认等于库存)

日期	奖品	权重	库存
3.1	1元	5000	5000
3.1	2元	1000	1000
3.1	3元	500	500
3.1	5元	100	100
3.1	iphone6s	1	1
3.1	未中奖	59409	59409

假设日活用户数为3万每个用户可抽3次
java代码

final Map<String, Integer> awardStockMap = new ConcurrentHashMap<>(); // 奖品 <--> 奖品库存
awardStockMap.put("1", 5000);
awardStockMap.put("2", 1000);
awardStockMap.put("3", 500);
awardStockMap.put("5", 100);
awardStockMap.put("iphone", 1);
awardStockMap.put("未中奖", 59409); //6601*10 -6601
//权重默认等于库存      
final Map<String, Integer> awardWeightMap = new ConcurrentHashMap<>(awardStockMap); // 奖品 <--> 奖品权重
 
int userNum = 30000; // 日活用户数
int drawNum = userNum * 3; // 每天抽奖次数 = 日活数*抽奖次数
Map<String, Integer> dailyWinCountMap = new ConcurrentHashMap<>(); // 每天实际中奖计数
for(int j=0; j<drawNum; j++){ // 模拟每次抽奖
    //排除掉库存为0的奖品
    Map<String, Integer> awardWeightHaveStockMap = awardWeightMap.entrySet().stream().filter(e->awardStockMap.get(e.getKey())>0).collect(Collectors.toMap(e->e.getKey(), e->e.getValue()));
    int totalWeight = (int) awardWeightHaveStockMap.values().stream().collect(Collectors.summarizingInt(i->i)).getSum();
    int randNum = new Random().nextInt(totalWeight); //生成一个随机数
    int prev = 0;
    String choosedAward = null;
    // 按照权重计算中奖区间
    for(Entry<String,Integer> e : awardWeightHaveStockMap.entrySet() ){
        if(randNum>=prev && randNum<prev+e.getValue()){
            choosedAward = e.getKey(); //落入该奖品区间
            break;
        }
        prev = prev+e.getValue();
    }
    dailyWinCountMap.compute(choosedAward, (k,v)->v==null?1:v+1); //中奖计数 
    if(!"未中奖".equals(choosedAward)){ //未中奖不用减库存 
        awardStockMap.compute(choosedAward, (k,v)->v-1); //奖品库存一
        if(awardStockMap.get(choosedAward)==0){
            System.out.printf("奖品：%s 库存为空%n",choosedAward); //记录库存为空的顺序
        }
    }
 
}
System.out.println("各奖品中奖计数: "+dailyWinCountMap); //每日各奖品中奖计数

输出

奖品：iphone 库存为空
奖品：5 库存为空
奖品：1 库存为空
奖品：2 库存为空
奖品：3 库存为空
每日各奖品中奖计数: {1=5000, 2=1000, 3=500, 5=100, iphone=1, 未中奖=83399}

可知假如该天抽奖次数能有9万次的话可以抽完所有的奖品另外因是单线程未考虑减库存
失败的情况即并发减库存的情况

抽奖算法2 存在奖品库存的前提下保证每次中奖的概率恒定如15% 抽100次有15次中奖

        final Map<String, Integer> awardStockMap = new ConcurrentHashMap<>(); 
        awardStockMap.put("1", 3000);
        awardStockMap.put("2", 2000);
        awardStockMap.put("3", 1500);
        awardStockMap.put("5", 1000);
        awardStockMap.put("10", 100);
        awardStockMap.put("20", 10);
        awardStockMap.put("50", 5);
        awardStockMap.put("100", 2);
        // 权重默认等于库存
        final Map<String, Integer> awardWeightMap = new ConcurrentHashMap<>(awardStockMap); 
        final Map<String, Integer> initAwardStockMap = new ConcurrentHashMap<>(awardStockMap); 

        int drawNum = 50780; // 理论可以抽完所有奖品所需抽奖次数 = 奖品数×中奖概率导数 = 7617*100/15
        final int threshold = 15; //中奖概率 15%
        Map<String, Integer> dailyWinCountMap = new ConcurrentHashMap<>(); // 每天实际中奖计数

        for (int j = 0; j < drawNum; j++) { // 模拟每次抽奖
            //确定是否中奖
            int randNum = new Random().nextInt(100);
            if(randNum>threshold){
                dailyWinCountMap.compute("未中奖", (k,v)->v==null?1:v+1);
                continue; //未中奖
            }
            //中奖 确定是哪个奖品
            //排除掉库存为0的奖品
            Map<String, Integer> awardWeightHaveStockMap = awardWeightMap.entrySet().stream().filter(e->awardStockMap.get(e.getKey())>0).collect(Collectors.toMap(e->e.getKey(), e->e.getValue()));
            if(awardWeightHaveStockMap.isEmpty()){ //奖池已为空
                System.out.printf("第%d次抽奖 奖品已被抽完%n",j);
                break;
            }
            int totalWeight = (int) awardWeightHaveStockMap.values().stream().collect(Collectors.summarizingInt(i->i)).getSum();
            randNum = new Random().nextInt(totalWeight); 
            int prev=0;
            String choosedAward = null;
            for(Entry<String,Integer> e : awardWeightHaveStockMap.entrySet() ){
                if(randNum>=prev && randNum<prev+e.getValue()){
                    choosedAward = e.getKey(); //落入此区间 中奖
                    dailyWinCountMap.compute(choosedAward, (k,v)->v==null?1:v+1);
                    break;
                }
                prev = prev+e.getValue();
            }
            //减小库存
            awardStockMap.compute(choosedAward, (k,v)->v-1);
        }
        System.out.println("每日各奖品中奖计数: "); // 每日各奖品中奖计数
        dailyWinCountMap.entrySet().stream().sorted((e1,e2)->e2.getValue()-e1.getValue()).forEach(System.out::println);
        awardStockMap.forEach((k,v)->{if(v>0){
            System.out.printf("奖品：%s, 总库存： %d, 剩余库存： %d%n",k,initAwardStockMap.get(k),v);
        }});

输出

第47495次抽奖 奖品已被抽完
每日各奖品中奖计数: 
未中奖=39878
1=3000
2=2000
3=1500
5=1000
10=100
20=10
50=5
100=2

可见实际不用到理论抽奖次数即可抽完所有奖品

https://segmentfault.com/a/1190000004502605

序号	奖品名称	奖品编号	抽到的概率
1	再来一次	P1	0.2
2	本站VIP一年	P2	0.1
3	谢谢参与	P3	0.4
4	50金币	P4	0.3
5	Iphone 6	P5	0.0
6	Ipad Air2	P6	-0.1
7	100元手机话费	P7	0.008

数据很简单，那么就直接看代码了

/**
 * 奖品类
 * @author:rex
 * @date:2014年10月20日
 * @version:1.0
 */
public class Gift {
	
	private int index;
	private String gitfId;
	private String giftName;
	private double probability;

	public Gift(int index, String gitfId, String giftName, double probability) {
		this.index = index;
		this.gitfId = gitfId;
		this.giftName = giftName;
		this.probability = probability;
	}

	public int getIndex() {
		return index;
	}

	public void setIndex(int index) {
		this.index = index;
	}

	public String getGitfId() {
		return gitfId;
	}

	public void setGitfId(String gitfId) {
		this.gitfId = gitfId;
	}

	public String getGiftName() {
		return giftName;
	}

	public void setGiftName(String giftName) {
		this.giftName = giftName;
	}

	public double getProbability() {
		return probability;
	}

	public void setProbability(double probability) {
		this.probability = probability;
	}

	@Override
	public String toString() {
		return "Gift [index=" + index + ", gitfId=" + gitfId + ", giftName=" + giftName + ", probability="
				+ probability + "]";
	}

}

/**
 * 不同概率抽奖工具包
 * @author:rex
 * @date:2014年10月20日
 * @version:1.0
 */
public class LotteryUtil {
	/**
	 * 抽奖
	 *
	 * @param orignalRates 原始的概率列表，保证顺序和实际物品对应
	 * @return 物品的索引
	 */
	public static int lottery(List<Double> orignalRates) {
		if (orignalRates == null || orignalRates.isEmpty()) {
			return -1;
		}

		int size = orignalRates.size();

		// 计算总概率，这样可以保证不一定总概率是1
		double sumRate = 0d;
		for (double rate : orignalRates) {
			sumRate += rate;
		}

		// 计算每个物品在总概率的基础下的概率情况
		List<Double> sortOrignalRates = new ArrayList<Double>(size);
		Double tempSumRate = 0d;
		for (double rate : orignalRates) {
			tempSumRate += rate;
			sortOrignalRates.add(tempSumRate / sumRate);
		}

		// 根据区块值来获取抽取到的物品索引
		double nextDouble = Math.random();
		sortOrignalRates.add(nextDouble);
		Collections.sort(sortOrignalRates);

		return sortOrignalRates.indexOf(nextDouble);
	}
	
	public static int getJD(List<Double> orignalRates) {
		if (orignalRates == null || orignalRates.isEmpty()) {
			return -1;
		}

		int size = orignalRates.size();

		// 计算总概率，这样可以保证不一定总概率是1
		double sumRate = 0d;
		for (double rate : orignalRates) {
			sumRate += rate;
		}

		// 计算每个物品在总概率的基础下的概率情况
		List<Double> sortOrignalRates = new ArrayList<Double>(size);
		Double tempSumRate = 0d;
		for (double rate : orignalRates) {
			tempSumRate += rate;
			sortOrignalRates.add(tempSumRate / sumRate);
		}

		// 根据区块值来获取抽取到的物品索引
		double nextDouble = Math.random();
		sortOrignalRates.add(nextDouble);
		Collections.sort(sortOrignalRates);

		return sortOrignalRates.indexOf(nextDouble);
	}
	
}

/**
 * 不同概率抽奖
 * @author:rex
 * @date:2014年10月20日
 * @version:1.0
 */
public class LotteryTest {
	public static void main(String[] args) {
		
		List<Gift> gifts = new ArrayList<Gift>();
		// 序号==物品Id==物品名称==概率
		gifts.add(new Gift(1, "P1", "物品1", 0.2d));
		gifts.add(new Gift(2, "P2", "物品2", 0.2d));
		gifts.add(new Gift(3, "P3", "物品3", 0.4d));
		gifts.add(new Gift(4, "P4", "物品4", 0.3d));
		gifts.add(new Gift(5, "P5", "物品5", 0d));
		gifts.add(new Gift(6, "P6", "物品6", -0.1d));
		gifts.add(new Gift(7, "P7", "物品7", 0.008d));

		List<Double> orignalRates = new ArrayList<Double>(gifts.size());
		for (Gift gift : gifts) {
			double probability = gift.getProbability();
			if (probability < 0) {
				probability = 0;
			}
			orignalRates.add(probability);
		}
		
		// statistics
		Map<Integer, Integer> count = new HashMap<Integer, Integer>();
		double num = 1000000;
		for (int i = 0; i < num; i++) {
			int orignalIndex = LotteryUtil.lottery(orignalRates);

			Integer value = count.get(orignalIndex);
			count.put(orignalIndex, value == null ? 1 : value + 1);
		}

		for (Entry<Integer, Integer> entry : count.entrySet()) {
			System.out.println(gifts.get(entry.getKey()) + ", count=" + entry.getValue() + ", probability="
					+ entry.getValue() / num);
		}
	}

}

输出

Gift [index=1, gitfId=P1, giftName=物品1, probability=0.2], count=180854, probability=0.180854
Gift [index=2, gitfId=P2, giftName=物品2, probability=0.2], count=180789, probability=0.180789
Gift [index=3, gitfId=P3, giftName=物品3, probability=0.4], count=361198, probability=0.361198
Gift [index=4, gitfId=P4, giftName=物品4, probability=0.3], count=269950, probability=0.26995
Gift [index=7, gitfId=P7, giftName=物品7, probability=0.008], count=7209, probability=0.007209

不同概率的抽奖原理很简单
就是把0到1的区间分块，而分块的依据就是物品占整个的比重，再根据随机数种子来产生0-1中间的某个数，来判断这个数是落在哪个区间上，而对应的就是抽到了那个物品。随机数理论上是概率均等的，产生的每个数理论上也应该概率均等，那么相应的区间所含数的多少就体现了抽奖物品概率的不同。（p.s. 当然数目是数不清楚的，具体抽象话了点）

这个实例的数据可以说明
1. 概率可以是负数和0，当然实际上中应该不会（p.s. 正常情况下可能真的有0，比如抽个iphone5，当然是抽不到的了，这个时候，构建礼物（List gifts）的时候最好就不要加这个进去），还有可以把负数的处理放到抽奖工具类(LotteryUtil)中；
2. 所有礼物加起来的概率可以不是1，可以认为这里的概率是一个权重。

转载至：http://www.blogjava.net/lishunli/archive/2012/10/17/389763.html

https://my.oschina.net/biezhi/blog/335481

java简单的抽奖方法——配置概率（100以内随机数的一个解决方案）

用户抽奖的大致思路就是，当用户点击抽奖后，后台随机算出100以内的一个随机数，然后查看该随机数是否在中奖概率范围内。

抽奖概率写死的方法：

/**
     * 抽奖概率
     *
     * @return rand
     */
    public static int randomInt() {
        int randomNum = new Random().nextInt(100) + 1;
        if (randomNum == 1) {
            return 1;
        } else if (randomNum >= 2 && randomNum <= 5) {
            return 2;
        } else if (randomNum >= 6 && randomNum <= 10) {
            return 3;
        } else if (randomNum >= 11 && randomNum <= 50) {
            return 4;
        } else {
            return 5;
        }

    }

从数据库读取概率配置（本次抽奖分五等奖）

public static int randomInt(LotteryPrizeEntry lotteryPrize) {
    //概率不能为空，至少为0
    if (lotteryPrize.getFirstPrize() + lotteryPrize.getSecondPrize()
            + lotteryPrize.getThirdPrize() + lotteryPrize.getFourthPrize() + lotteryPrize.getFifthPrize() > 100) {
        return 0;
    }
    int randomNum = new Random().nextInt(100) + 1;
    List<Integer> list = new ArrayList<Integer>();
    list.add(lotteryPrize.getFirstPrize());
    list.add(lotteryPrize.getSecondPrize());
    list.add(lotteryPrize.getThirdPrize());
    list.add(lotteryPrize.getFourthPrize());
    list.add(lotteryPrize.getFifthPrize());
    int prize = 1; //奖品级数
    int num = 0; //存中奖概率数
    int num2 = 1;//存中奖概率数
    for (Integer i : list) {
        num = +i;
        if (i >= 1) {
            if (randomNum >= num2 && randomNum <= num) {
                return prize;
            }
        }
        prize++; //奖级加一
        num2 = +i;
    }
    return prize;
中奖概率配置表：
BEGIN_TIME        DATE                开始时间
END_TIME         DATE                结束时间
LOTTERY_ISENABLE        NUMBER                 是否开启 0关闭1开启
FIRST_PRIZE        NUMBER                一等奖概率
SECOND_PRIZE         NUMBER                 二等奖概率
THIRD_PRIZE         NUMBER                三等奖概率
FOURTH_PRIZE         NUMBER                 四等奖概率
FIFTH_PRIZE         NUMBER                 五等奖概率
http://www.zui da ima.com/share/2933089644039168.htm

权重随机算法的java实现一、概述　　平时，经常会遇到权重随机算法，从不同权重的N个元素中随机选择一个，并使得总体选择结果是按照权重分布的。如广告投放、负载均衡等。
　　如有4个元素A、B、C、D，权重分别为1、2、3、4，随机结果中A:B:C:D的比例要为1:2:3:4。
　　总体思路：累加每个元素的权重A(1)-B(3)-C(6)-D(10)，则4个元素的的权重管辖区间分别为[0,1)、[1,3)、[3,6)、[6,10)。然后随机出一个[0,10)之间的随机数。落在哪个区间，则该区间之后的元素即为按权重命中的元素。
　　实现方法：
利用TreeMap，则构造出的一个树为:
　　　　B(3)
　　　 /      
        /         
     A(1)     D(10)
               /
             /
         C(6)
然后，利用treemap.tailMap().firstKey()即可找到目标元素。
当然，也可以利用数组+二分查找来实现。
二、源码



package com.xxx.utils;
 
import com.google.common.base.Preconditions;
import org.apache.commons.math3.util.Pair;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;
 
import java.util.List;
import java.util.SortedMap;
import java.util.TreeMap;
 
 
public class WeightRandom<K,V extends Number> {
    private TreeMap<Double, K> weightMap = new TreeMap<Double, K>();
    private static final Logger logger = LoggerFactory.getLogger(WeightRandom.class);
 
    public WeightRandom(List<Pair<K, V>> list) {
        Preconditions.checkNotNull(list, "list can NOT be null!");
        for (Pair<K, V> pair : list) {
            double lastWeight = this.weightMap.size() == 0 ? 0 : this.weightMap.lastKey().doubleValue();//统一转为double
            this.weightMap.put(pair.getValue().doubleValue() + lastWeight, pair.getKey());//权重累加
        }
    }
 
    public K random() {
        double randomWeight = this.weightMap.lastKey() * Math.random();
        SortedMap<Double, K> tailMap = this.weightMap.tailMap(randomWeight, false);
        return this.weightMap.get(tailMap.firstKey());
    }
 
}















　　
　　
三、性能4个元素A、B、C、D，其权重分别为1、2、3、4，运行1亿次，结果如下：


元素
命中次数
误差率





A
10004296
0.0430%





B
19991132
0.0443%





C
30000882
0.0029%





D
40003690
0.0092%









从结果，可以看出，准确率在99.95%以上。
四、另一种实现利用B+树的原理。叶子结点存放元素，非叶子结点用于索引。非叶子结点有两个属性，分别保存左右子树的累加权重。如下图：
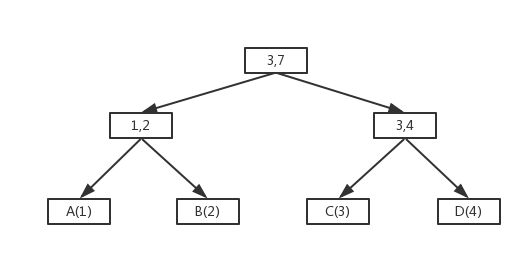
看到这个图，聪明的你应该知道怎么随机了吧。
此方法的优点是：更改一个元素，只须修改该元素到根结点那半部分的权值即可。
end
作者：水岩
出处：http://www.cnblogs.com/waterystone/
两类，第一类是常见的有等级的抽奖活动，如一等、二等、三等奖等等，废话不多说，直接贴代码：
推荐：简单抽奖用的算法
[/* 每种奖品的概率          * 总概率为333          * */         int a1 = 1;         int a4 = 200;         int a6 = 50;         int a8 = 1;         int a9
// 分别为一、二、三、四等将的奖品数量，最后一个为未中奖的数量。
    private static final Integer[] lotteryList = {5, 10, 20, 40, 100};

    private int getSum() {
        int sum = 0;
        for (int v : lotteryList) {
            sum += v;
        }
        return sum;
    }

    private int getLotteryLevel() {
        Random random = new Random(System.nanoTime());
        int sum = getSum();
        for (int i = 0; i < lotteryList.length; ++i) {
            int randNum = Math.abs(random.nextInt()) % sum;
            if (randNum <= lotteryList[i]) {
                return i;
            } else {
                sum -= lotteryList[i];
            }
        }
        return -1;
    }另一类是不分等级的抽奖活动，仅需要参与人数与奖品总数，各奖品中奖概率相等。代码如下：
//另一种抽奖算法，用于公司抽奖，即总参与人数与奖品数固定。
    private static final int lotteryNum = 75;
    private static final int total = 175;
    private static Set<Integer> lotterySet = new HashSet<Integer>();
    static {
        for (int i=1; i <= lotteryNum; ++i) {
            lotterySet.add(total*i/lotteryNum);
        }
    }
    private int getLotteryNum2() {
        Random rand = new Random(System.nanoTime());
        int randNum = Math.abs(rand.nextInt()) % total;
        if (lotterySet.contains(randNum)) {
            return randNum*lotteryNum/total;
        }
        return -1;
    }
http://www.itboth.com/d/6R3YJr/java
 

查看全文

相关阅读:
记录idea run dashboard设置（微服务项目多服务启动）
记录Java8中的字符串转数组再通过指定符号拼接
 Java 调用底层接口的几种方法
 工作两个月以后的感想
 几种开源工作流引擎的简单比较
 labin编译的另一种方式
 最近参加一个团队创业项目的感触
 gof设计模式——生成器c++实现
 gof设计模式——抽象工厂 c++实现
 几种开源网络爬虫的简单比较

原文地址：https://www.cnblogs.com/softidea/p/10002359.html

元素	命中次数	误差率
A	10004296	0.0430%
B	19991132	0.0443%
C	30000882	0.0029%
D	40003690	0.0092%

JAVA基于权重的抽奖

https://www.cnblogs.com/younggun/p/3249772.html

简介

效果图

业务要求

实现方法

抽奖的业务逻辑代码如下

前端抽奖工具类

前端js调用抽奖类

以上是抽奖的主要代码

Java抽奖概率算法

java简单的抽奖方法——配置概率（100以内随机数的一个解决方案）

权重随机算法的java实现

一、概述

二、源码

三、性能

四、另一种实现