8.20模拟赛再次观光记

T1

传教士

Description

panzhili 王国的疆土恰好是一个矩形，为了管理方便，国王 jjs 将整个疆土划分成 N＊M块大小相同的区域。由于 jjs 希望他的子民也能信教爱教（”打拳”神教），所以他想安排一些传教士到全国各地去传教。但这些传教士的传教形式非常怪异，他们只在自己据点周围特定的区域内传教且领地意识极其强烈 （即任意一个传教士的据点都不能在其他传教士的传教区域内，否则就会发生冲突）。现在我们知道传教士的传教区域为以其据点为中心的两条斜对角线上（如图）。现在 jjs 请你帮忙找出一个合理的安置方案，使得可以在全国范围内安置尽可能多的传教士而又不至于任意两个传教士会发生冲突。

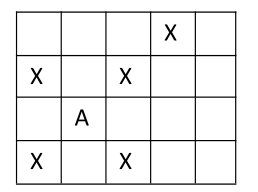
（若 A 为某传教士的据点，则其传教范围为所有标有 X 的格子。为不产生冲突，则第二个传教士的据点只能放在上图的空格中。）

Input

输入文件共一行，包含两个整数 N 和 M，代表国土的大小，n 为水平区域数，m 为垂直区域数。

Output

输出文件仅一行，包含一个整数，即最多可以安置的传教士的数目。

Sample Input

3 4

Sample Output

6

Hint

　　对于 100%的数据，1<=n,m<=9，且数据规模呈梯度上升。

woc？T1状压DP？那就设每行的状态为一个二进制数i，显然在一行内放多少个传教士都可以，O(2ⁿ)暴力扫。

如何判断两行不冲突呢？设x行的状态为i，y行的状态为j，只需要判断(i>>abs(x-y)&j)||(i<<abs(x,y)&j)就行了，相当与把两行的状态错开行数之差那么多在与起来。

冷静想了想，好像还DP不起，因为对于当前行x,要知道前x-1行的所有状态。

我还怕你吗？DP写不了，DFS还是可以的，于是我们的状压搜索就诞生了。

#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
inline int read() {
    char ch;
    bool bj=0;
    while(!isdigit(ch=getchar()))
        bj|=(ch=='-');
    int res=ch^(3<<4);
    while(isdigit(ch=getchar()))
        res=(res<<1)+(res<<3)+(ch^(3<<4));
    return bj?-res:res;
}
void printnum(int x) {
    if(x>9)printnum(x/10);
    putchar(x%10+'0');
}
inline void print(int x,char ch) {
    if(x<0) {
        putchar('-');
        x=-x;
    }
    printnum(x);
    putchar(ch);
}
int s[520],t[520],cnt;
int n,m;
int a[10];
int ans=0;
inline int lowbit(int x) {
    return x&(-x);
}
inline int count(int x) {
    int tmp=0;
    while(x) {
        x-=lowbit(x);
        tmp++;
    }
    return tmp;
}
inline bool check(int i,int pos) {
    for(int x=1; x<pos; x++)
        if(((a[x]>>(pos-x))&s[i])||((a[x]<<(pos-x))&s[i]))return 0;
    return 1;
}
void DFS(int pos,int tot) {
    if(pos==n+1) {
        ans=max(ans,tot);
        return;
    }
    for(int i=1; i<=cnt; i++)
        if(check(i,pos)) {
            a[pos]=s[i];
            DFS(pos+1,tot+t[i]);
        }
}
int main() {
    n=read();
    m=read();
    for(int i=0; i<=(1<<m)-1; i++) {
        s[++cnt]=i;
        t[cnt]=count(i);
    }
    DFS(1,0);
    cout<<ans<<" ";
    return 0;
}

这个代码肯定稳稳T掉呀，但看到如此小的数据范围，直接让它挂机打表就行了，献上AC程序。

#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
inline int read() {
    char ch;
    bool bj=0;
    while(!isdigit(ch=getchar()))
        bj|=(ch=='-');
    int res=ch^(3<<4);
    while(isdigit(ch=getchar()))
        res=(res<<1)+(res<<3)+(ch^(3<<4));
    return bj?-res:res;
}
void printnum(int x) {
    if(x>9)printnum(x/10);
    putchar(x%10+'0');
}
inline void print(int x,char ch) {
    if(x<0) {
        putchar('-');
        x=-x;
    }
    printnum(x);
    putchar(ch);
}
int ans[9][9]= {1,2,3,4,5,6,7,8,9,
                2,2,4,4,6,6,8,8,10,
                3,4,4,6,7,8,9,10,11,
                4,4,6,6,8,8,10,10,12,
                5,6,7,8,8,10,11,12,13,
                6,6,8,8,10,10,12,12,14,
                7,8,9,10,11,12,12,14,15,
                8,8,10,10,12,12,14,14,16,
                9,10,11,12,13,14,15,16,16,
               };
int n,m;
int main() {
    n=read()-1;
    m=read()-1;
    print(ans[n][m],'
');
    return 0;
}

规律？不想找，等数据范围大点再说吧……

 T2

czy把妹

Description

　　Czy 是个大丧失，非常喜欢 bm。他经常挑战 bm 的极限，同时 b 很多的 mz这一天，czy 又开始了他的极限挑战。在一个数轴上有 n 个 maze,她们都在等待着 czy 的到来。Czy 一开始站在 k 号妹子的旁边，他需要搞定所有的妹子(由于他向 fewdan 学会了绝技，所以搞定妹子的时间是无限接近于 0 的，也就是一瞬间就搞定而不用花额外的时间)。Maze 们都很没有耐心，每让她们多等 1s,她们就会增加 w[i]的不开心值。现在，czy 从 k号妹子这里出发，以 1m/s 的速度开始行动，他希望在搞定所有 maze 的情况下使得她们的不开心值总和最小，于是他找到了即将在 NOIP2019 AK 的你来帮他解决这个问题。

Input

　　输入文件的第一行包含一个整数 N，2<=N<=1000，表示 maze 的数量。
　　第二行包含一个整数 V，1<=V<=N，表示开始时 czy 站在几号 maze 的旁边.接下来的N 行中。
　　每行包含两个用空格隔开的整数 D 和 W，用来描述每个 maze，其中 0<=D<=1000，0<=W<=1000。
　　D 表示 MM 在数轴上的位置(单位: m)，W 表示每秒钟会增加的不开心值。

Output

　　一个整数，最小的不开心值。(答案不超过 10^9)

Sample Input

4
3
2 2
5 8
6 1
8 7

Sample Output

56

Hint

　　对于 40%的数据：1<=n<=7
　　对于 100%的数据：1<=n<=1000 0<=D<=1000 0<=w<=1000

40pts：把他b每个maze的顺序枚举出来，暴力算，复杂度O(n!)。

???pts：贪心，cmp函数以(cal(x,now)*a[y].w<cal(y,now)*a[x].w)排序，(cal函数算的是距离)，删数组头并用它更新now，得到的序列既是最优解序列，复杂度O(n²)

本式没有传递性，所以正确性不能保证。笔者考试写了这个，幸好没有赌那一把，实测0分。

???pts：DP，设f[i][j]为第i个选择j的最优解，g[i][j]为第i个选择j时未选mm的w累和

f[i][j]=f[i-1][k]+cal(j,k)×g[i-1][k]

g[i][j]=g[i-1][k]-w[j](k为f[i][j]最优转移的k)

初始：g[1][begin]=Σw[i] -w[begin]，f[1][begin]=1;

答案：min{f[n][i]}

笔者不知道如何判断从(i-1,k)转移的时候如何判断这个状态不含j本身，GG。

100pts：区间DP，设f[i][j]为[i,j]这段区间的mm处理完的最优解，此时czy在i，f[j][i]反之。

因为这是区间DP，DP的阶段以区间长度划分。

考虑我能从哪来？

f[i][j]可以由f[i+1][j]直接走过来，还可以由f[j-1][i]走到j再走到i。

为什么有第二种情况呢？有人觉得这样一定不比f[i+1][j]走过来优。但这样一是提防极端数据，二是保证DP的完整性。按照我个人对DP的理解，你只要有正确的初始化，全面的状态转移和如何统计答案，无论中间的过程多么匪夷所思，交给你的程序就行了(当然DP的优化另当别论)

f[j][i]同理。

设cal(x,y)为[x,y]中w[i]的和

f[i][j]=min(f[i+1][j]+(a[i+1].d-a[i].d)*(cal(1,i)+cal(j+1,n)),f[j-1][i]+(a[j].d-a[j-1].d)*(cal(1,i-1)+cal(j,n))+(a[j].d-a[i].d)*(cal(1,i-1)+cal(j+1,n)))

f[j][i]=min(f[j-1][i]+(a[j].d-a[j-1].d)*(cal(1,i-1)+cal(j,n)),f[i+1][j]+(a[i+1].d-a[i].d)*(cal(1,i)+cal(j+1,n))+(a[j].d-a[i].d)*(cal(1,i-1)+cal(j+1,n)))

看起来很复杂，理解了也大同小异。

谈谈初始化。

f[i][i]=cal(1,n)×abs(a[i].d-a[begin].d)

意思是i这个点有begin走过来所需时间。可能有人又会问了(没错，这个sb就是我)，既然你是从begin走过来的，怎么不是f[i][begin]或f[begin][i]=cal(1,n)×abs(a[i].d-a[begin].d)呢？

咳咳，我们要求的是f[i][i]，其余的东西又不管。注意定义是"[i,j]这段区间的mm处理完"，czy虽然从begin过来，我们可以认为[i+1,begin]中间的mm他一个都没理。

尽管这很奇怪，因为他一开始就站在begin却不把(近在咫尺的)mm泡了而去浪费时间，但f[i][i]定义不包括begin，我们就不必找些毒瘤来玩。

答案：min(f[1][n],f[n][1])

总结：不要相信自己的直觉，相信理性，虽然这不和常理，但它不仅有效，还正确。

#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define INF 0x3f3f3f3f
inline int read() {
    char ch;
    bool bj=0;
    while(!isdigit(ch=getchar()))
        bj|=(ch=='-');
    int res=ch^(3<<4);
    while(isdigit(ch=getchar()))
        res=(res<<1)+(res<<3)+(ch^(3<<4));
    return bj?-res:res;
}
struct node {
    int w,d,id;
    bool operator < (node x)const {
        return d<x.d;
    }
} a[1005];
int n,st,f[1005][1005],sum[1005];
inline int cal(int x,int y) {
    return sum[y]-sum[x-1];
}
signed main() {
    n=read();
    st=read();
    for(int i=1; i<=n; i++) {
        a[i].d=read();
        a[i].w=read();
        a[i].id=i;
    }
    sort(a+1,a+n+1);    
    for(int i=1; i<=n; i++)
        if(a[i].id==st) {
            st=i;
            break;
        }
    for(int i=1; i<=n; i++)sum[i]=sum[i-1]+a[i].w;
    memset(f,0x3f,sizeof(f));
    for(int i=1; i<=n; i++)f[i][i]=sum[n]*abs(a[i].d-a[st].d);
    for(int len=2; len<=n; len++)
        for(int i=1; i<=n-len+1; i++) {
            int j=i+len-1;
            f[i][j]=min(f[i+1][j]+(a[i+1].d-a[i].d)*(cal(1,i)+cal(j+1,n)),f[j-1][i]+(a[j].d-a[j-1].d)*(cal(1,i-1)+cal(j,n))+(a[j].d-a[i].d)*(cal(1,i-1)+cal(j+1,n)));
            f[j][i]=min(f[j-1][i]+(a[j].d-a[j-1].d)*(cal(1,i-1)+cal(j,n)),f[i+1][j]+(a[i+1].d-a[i].d)*(cal(1,i)+cal(j+1,n))+(a[j].d-a[i].d)*(cal(1,i-1)+cal(j+1,n)));
        }
    cout<<min(f[1][n],f[n][1])<<endl;
    return 0;
}

P.S.关于输入的D是否有序，题目未做描述，即可默认无序。虽然数据有假，但是要坚持题目原意。

 T3

 [国家集训队]跳跳棋

题目链接

Description

　　某跳跳棋游戏是在一条数轴上进行的。 棋子只能摆在整点上。 每个点不能摆超过一个棋子。
　　某一天，黄金大神和 cjy 用跳跳棋来做一个简单的游戏：棋盘上有 3 颗棋子，分别在 a，b，c 这三个位置。他们要通过最少的跳动把它们的位置移动成 x，y，z。（棋子是没有区别的）
　　跳动的规则很简单，任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过 1 颗棋子。

我们用跳跳棋来做一个简单的游戏：棋盘上有3颗棋子，分别在a，b，c这三个位置。我们要通过最少的跳动把他们的位置移动成x，y，z。（棋子是没有区别的）

跳动的规则很简单，任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。

写一个程序，首先判断是否可以完成任务。如果可以，输出最少需要的跳动次数。

Input

第一行包含三个整数，表示当前棋子的位置a b c。（互不相同）

第二行包含三个整数，表示目标位置x y z。（互不相同）

Output

如果无解，输出一行NO。

如果可以到达，第一行输出YES，第二行输出最少步数。

Sample Input

1 2 3
0 3 5

Sample Output

YES
2

Hint

　　对于 20%的数据，输入整数的绝对值均不超过 10
　　对于 40%的数据，输入整数的绝对值均不超过 10000
　　对于 100%的数据，绝对值不超过 109

 

20pts：宽搜即可

100pts：说实话，你再给我一天我都想不出来

设当前状态为{a,b,c}，只有三种移动方式

1、b以a为轴向左跳

2、b以c为轴向右跳

3、a,c中距离b较小的以b为轴跳(因为一次只能跳过一个棋子)

假设我们有一棵搜索树，当前节点是{a,b,c}，我们把情况1、2视做它的两个子节点，3视作它的父亲。

显然，若a到b的距离等于b到c的距离时，这个状态就是树根，因为它没有父亲。

问题就转化为了求树上两节点的距离，自然而然地想到了LCA

设cal(a,k)为状态a向上跳k次到达的状态，若跳k次超出了根节点，则返回根节点。解决了cal函数，就解决了这道题。

因为LCA是不停地向上爬的，所以只用考虑情况3式转移

设t1=b-a，t2=c-b，相对位置很好理解吧。

如果t1=t2，此节点是根，直接返回即可。

如果t1<t2，所以只能是a以b为轴向右跳，我们此时再算一下相对位置，t1'还是t1，唯有t2'=t2-t1。

能向上跳多少次呢？也就是t2%t1次，但如果t2=n×t1,实际上跳n-1次就到根了，我们需要完善一下，即(t2-1)%t1,大家可以手玩一下。

如果t1>t2同理。

这个问题可以分成若干个字问题，递归解决。

有了cal函数以后，就可以由求LCA一样解决了：先调整到同一高度，再二分向上的距离。

#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define int long long
inline int read() {
    char ch;
    bool bj=0;
    while(!isdigit(ch=getchar()))
        bj|=(ch=='-');
    int res=ch^(3<<4);
    while(isdigit(ch=getchar()))
        res=(res<<1)+(res<<3)+(ch^(3<<4));
    return bj?-res:res;
}
void printnum(int x) {
    if(x>9)printnum(x/10);
    putchar(x%10+'0');
}
inline void print(int x,char ch) {
    if(x<0) {
        putchar('-');
        x=-x;
    }
    printnum(x);
    putchar(ch);
}
struct node {
    int s[5];
    inline void set() {
        sort(s+1,s+4);
    }
    inline bool operator != (node x)const {
        for(int i=1; i<=3; i++)
            if(s[i]!=x.s[i])return 1;
        return 0;
    }
} st,ed;
inline node cal(node x,int k,int &depth) {
    node ans=x;
    int t1=x.s[2]-x.s[1],t2=x.s[3]-x.s[2];
    if(t1==t2)return x;
    if(t1<t2) {
        int tmp=min(k,(t2-1)/t1);
        k-=tmp;
        depth+=tmp;
        ans.s[2]+=tmp*t1;
        ans.s[1]+=tmp*t1;
    } else {
        int tmp=min(k,(t1-1)/t2);
        k-=tmp;
        depth+=tmp;
        ans.s[2]-=tmp*t2;
        ans.s[3]-=tmp*t2;
    }
    if(k)return cal(ans,k,depth);
    return ans;
}
int d1,d2,ans;
signed main() {
    st.s[1]=read();
    st.s[2]=read();
    st.s[3]=read();
    st.set();
    ed.s[1]=read();
    ed.s[2]=read();
    ed.s[3]=read();
    ed.set();
    node t1=cal(st,INF,d1);
    node t2=cal(ed,INF,d2);
    if(t1!=t2) {
        puts("NO");
        return 0;
    }
    if(d1>d2) {
        swap(d1,d2);
        swap(st,ed);
    }
    ans=d2-d1;
    int tmp1,tmp2;
    ed=cal(ed,ans,tmp1);
    int l=0,r=d1;
    while(l<=r) {
        int mid=(l+r)>>1;
        if(cal(st,mid,tmp1)!=cal(ed,mid,tmp2))l=mid+1;
        else r=mid-1;
    }
    puts("YES");
    print(ans+(l<<1),'
');
    return 0;
}

得分情况：100(100)+40(40)+5(10)=145(150)

OI尚未结束，蒟蒻仍需努力