0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
栈
| 栈的定义 |

| 栈存储结构 |
栈的顺序储存结构
定义一个top变量来指示栈顶元素在数组中的位置,它可以移动,意味着栈顶的可以变大可以变小。若存储栈的长度为StackSize,则栈顶的位置top必须小于StackSize。当栈中存在一个元素时,top = 0 ,把空栈的判定条件定为 top= -1 。
typedef struct SNode
{
int data[MAXSIZE];
int top;//栈顶指针,指向栈顶所在的位置
}SqStack;
栈的顺序储存结构之进栈
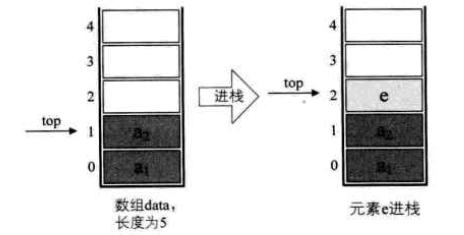
bool Push(SqStack &S,int e)
{
if(S->top == MAXSIZE - 1)
{
cout << "Stack Full" << endl; //栈满
return false;
}
S->top++;//因为空栈top为-1,所以top先增加后在该位置赋值
S->data[S->top] = e;
return true;
}
栈的顺序储存结构之出栈
bool Pop(SqStack &S,int &e)
{
if(S->top == -1)
{
cout << "Stack Empty" << endl;//栈空
return false;
}
e = S->data[S->top];
S->top--;
return true;
}
两栈共享存储空间
这个共享栈是针对于相同数据类型的栈。一个栈的栈底为数组的始端,即下标为0处,另一个栈为数组的末端,即下标为数组长度MAXSIZE-1处。这样,两个栈如果增加元素,就是两端点向中间延伸。top1和top2是栈1和栈2的栈顶指针。栈1,栈2都为空时, top1 = -1,top2 = MAXSIZE。在极端情况下,如果top1 = MAXSIZE-1时,表明栈1满了,栈2为空;top2 = 0时,表明栈2满了,栈1为空。但是更多的情况是,没有达到极限,而是top1、top2都存在移动,即判断栈满的情况则为:top1 + 1 = top2。
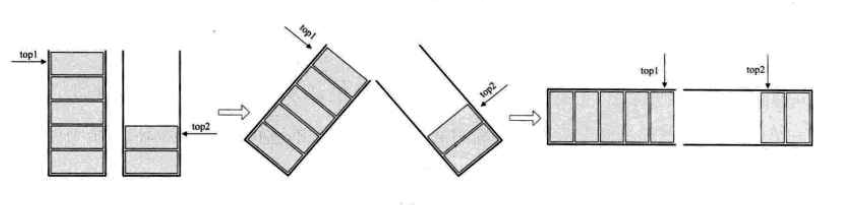
typedef struct SNode
{
int data[MAXSIZE];
int top1;
int top2;
}SqStack;
两栈共享存储空间之进栈
bool Push(SqStack &S,int e,int Number)
{
if(S->top1 + 1 == S->top2)
{
cout << "Stack FULL" << endl; //栈满
return false;
}
if(Number == 1)
{
S->top1++;
S->data[S->top1] = e;
}
if(Number == 2)
{
S->top2--;
S->data[S->top2] = e;
}
return true;
}
两栈共享存储空间之出栈
bool Pop(SqStack &S,int &e,int Number)
{
if(Number == 1)
{
if(S->top1 == -1)
{
cout << "Stack Empty" << endl; //栈1为空
return false;
}
e = S->data[S->top1];
S->top1--;
}
if(Number == 2)
{
if(s->top2 == MAXSIZE)
{
cout << "Stack Empty" << endl; //栈2为空
return false;
}
e = S->data[S->top2];
S->top2++;
}
return true;
}
栈的链式存储结构
将链栈的栈顶放在了单链表的头部 ,且已经有了栈顶在头部,所以单链表不需要头节点。对于链栈来说,不存在栈满的情况。
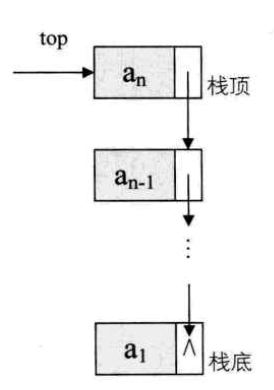
typedef struct StackNode
{
int data;
struct StackNode * next;
}StackNode, *LinkStackPtr;
typedef struct LinkStack
{
LinkStackPtr top;//栈顶指针
int count;//存放当前栈的元素个数
}LinkStack;
栈的链式存储结构之进栈
bool Push(LinkStack &S,int e)
{
LinkStackPtr temp
temp = (LinkStackPtr) malloc(sizeof(StackNode));//在插入之前应该先申请一个节点
temp->data = e;
temp->next = S->top;//将当前的栈顶元素赋值给新的直接后继
S->top = temp;//将新的栈顶元素赋值给s
S->count++;
return true;
}
栈的链式存储结构之出栈
bool Pop(LinkStack &S,int &e)
{
LinkStackPtr p;
if(StackEmpty(S))
{
cout << "Stack Empty" << endl; //栈为空
return false;
}
e = S->top->data;
p = S->top;
S->top = S->top->next;//将指针下移
free(p);
S->count--;//并将栈的元素个数减1
return true;
}
| 栈的应用 |
递归
字符串逆转
void strReverse(char s[],int len)
{
if(len==1)
printf(“%c”,s[0]);
else
{
printf(“%c”,s[len-1]);
strReverse(s,len-1);
}
}
进制转换
将输入的十进制数转化成八进制数
void conversion(int N)
{
int e;
LinkStack s;
InitStack(s);
while (N)
{
Push(s, N % 8);
N = N / 8;
}
while (!StackEmpty(s))
{
Pop(s, e);
cout << e;
}
}
符号配对
'()'、'[]'、'{}'是否正确配对
算法思想:
- 遇到左括号,将左括号逐一入栈
- 一旦碰到右括号,先判断栈顶是否为空,为空则不匹配,输出“NO”;不为空,判断是否与右括号配对,匹配成功则输出“YES”,匹配不成就输出“左括号和NO”
#include<iostream>
using namespace std;
#include<string>
#include<queue>
#include<stack>
#include<stdio.h>
int main()
{
string str;
stack<char> S;
int i;
cin >> str;
for (i = 0; str[i] != '�'; i++)
{
if (str[i] == '(' || str[i] == '[' || str[i] == '{')//只把括号类字符存入栈中
S.push(str[i]);
else if (str[i] == ')') //判断栈顶元素是否匹配
{
if (S.empty()) //如果栈顶为空则不配对
{
cout << "no";
return 0;
}
if (S.top() == '(')
S.pop();
}
else if (str[i] == ']') //判断栈顶元素是否匹配
{
if (S.empty()) //如果栈顶为空则不配对
{
cout << "no";
return 0;
}
if (S.top() == '[')
S.pop();
}
else if (str[i] == '}') //判断栈顶元素是否匹配
{
if (S.empty()) //如果栈顶为空则不配对
{
cout << "no";
return 0;
}
if (S.top() == '{')
S.pop();
}
}
if (!S.empty())
{
cout << S.top() << "
" << "no";
return 0;
}
cout << "yes"; //完成上述循坏栈空说明就是配对
return 0;
}
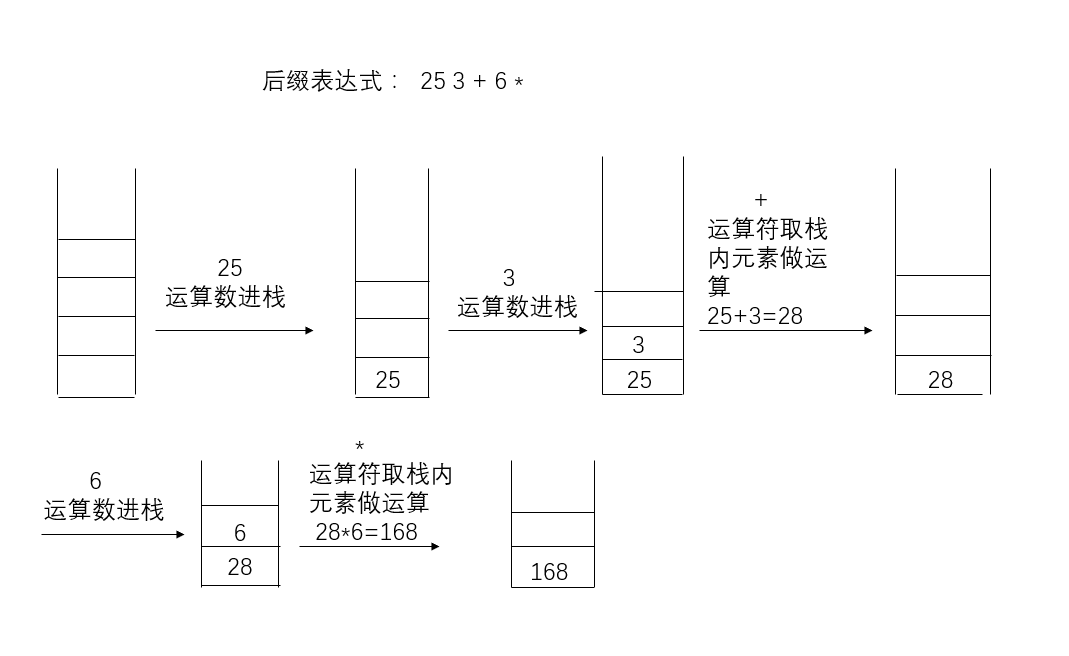
表达式求值
1、读入表达式一个字符
2、若是操作数,压入栈,
3、若是运算符,从栈中弹出2个数,将运算结果再压入栈
4、若表达式输入完毕,栈顶即表达式值;若表达式未输入完,转1
#include<iostream>
#include<stack>
#include<string>
using namespace std;
void compvalue(stack<int>& s, string postexp)
{
int i = 0, num = 0, temp1, temp2, flag, F = 0;
char ch1, ch2;
while (postexp[i])
{
ch1 = postexp[i];
if (ch1 >= '0' && ch1 <= '9')
{
num = ch1 - '0';
if (i != 0 & postexp[i - 1] >= '0' && postexp[i - 1] <= '9')
{
s.pop();
num = (postexp[i - 1] - '0') * 10 + num;
}
s.push(num);
}
if (ch1 == '+')
{
temp1 = s.top();
s.pop();
temp2 = s.top();
s.pop();
flag = temp1 + temp2;
s.push(flag);
}
if (ch1 == '-')
{
temp1 = s.top();
s.pop();
temp2 = s.top();
s.pop();
flag = temp2 - temp1;
s.push(flag);
}
if (ch1 == '*')
{
temp1 = s.top();
s.pop();
temp2 = s.top();
s.pop();
flag = temp1 * temp2;
s.push(flag);
}
if (ch1 == '/')
{
temp1 = s.top();
s.pop();
temp2 = s.top();
if (temp1 == 0)
{
cout << "divide error!";
while (!s.empty())
s.pop();
return;
}
s.pop();
flag = temp2 / temp1;
s.push(flag);
}
i++;
}
}
int main()
{
stack<int> s;
string str;
cin >> str;
compvalue(s, str);
cout << s.top();
return 0;
}
队列
| 队列的定义 |
单队列:
只允许在表的一端进行插入操作,而在另一端进行删除操作的线性表。队列是一种先进先出的线性表,简称FIFO。允许插入的一端是队尾,允许删除的一端是队头。
初始化:rear=front=-1
队满判断条件:Q->rear==MAXSIZE-1
队空判断条件:Q->rear - Q->front
队列长度计算:length=rear+1
循环队列:
头尾相接的队列的顺序存储结构。
初始化:rear=front=0
队满判断条件:(rear+1) % QueueSize = front
队空判断条件:rear=front
队列长度计算:length=(rear - front + QueueSize) % QueueSize
| 队列的存储结构 |
队列的顺序存储结构
typedef struct
{
int data[MAXSIZE];
int front;
int rear;
}SqQueue;
单队列的顺序存储结构之入队
bool EnQueue(SqQueue *Q,int e)
{
if(Q->rear==MAXSIZE-1)
{
cout << "Queue Full" << endl;
return false;
}
Q->rear++;
Q->data[Q->rear]=e;
return true;
}
单队列的顺序存储结构之出队
bool DeQueue(LinkQueue *Q,int *e)
{
if(Q->rear==Q->front)
{
cout << "Queue Empty" <<endl;
return false;
}
Q->front++;
e=Q->data[Q->front];
return true;
}
循环队列的顺序存储结构之入队
bool EnQueue(SqQueue *Q,int e)
{
if((Q->rear+1)%MAXSIZE==Q->front)
{
cout << "Queue Full" << endl;
return false;
}
Q->data[Q->rear]=e;
Q->rear=(Q->rear+1)%MAXSIZE;
return true;
}
循环队列的顺序存储结构之出队
bool DeQueue(LinkQueue *Q,int *e)
{
if(Q->rear==Q->front)
{
cout << "Queue Empty" <<endl;
return false;
}
e=Q->data[Q->front];
Q->front=(Q->front+1)%MAXSIZE;
return true;
}
队列的链式存储结构
typedef struct QNode
{
int data;
struct QNode *next;
}QNode,*QPtr;
typedef struct
{
QPtr front;
QPtr rear;
}LinkQueue;
队列的链式存储结构之入队
bool EnQueue(LinkQueue *Q,int e)
{
QPtr temp;
temp = (QPtr)malloc(sizeof(QNode));
temp->data=e;
temp->next=NULL;
Q->rear->next=temp;
Q->rear=temp;
return true;
}
队列的链式存储结构之出队
bool DeQueue(LinkQueue *Q,int *e)
{
QPtr temp;
if(Q->rear==Q->front)
{
cout<<"Queue Empty"<<endl;
return false;
}
temp=Q->front->next;
e=temp->data;
Q->front->next=temp->next;
if(Q->rear==temp)
Q->front=Q->rear;
return true;
}
| 队列的应用 |
舞伴问题
男队和女队,分别取队头配对,长度不等时,有一对多出未成功配对的舞者
int QueueLen(SqQueue Q)
{
return (Q->rear - Q->front);
}
int EnQueue(SqQueue& Q, Person e)
{
Q->data[Q->rear] = e;
Q->rear++;
return OK;
}
int QueueEmpty(SqQueue& Q)
{
if (Q->front == Q->rear)
return OK;
else
return ERROR;
}
int DeQueue(SqQueue& Q, Person& e)
{
if (QueueEmpty(Q))
return ERROR;
e = Q->data[Q->front];
Q->front++;
return OK;
}
void DancePartner(Person dancer[], int num)
{
int i;
Person temp;
for (i = 0; i < num; i++)
{
if (dancer[i].sex == 'F')
EnQueue(Fdancers, dancer[i]);
else
EnQueue(Mdancers, dancer[i]);
}
while (!QueueEmpty(Fdancers) && !QueueEmpty(Mdancers))
{
DeQueue(Fdancers, temp);
cout << temp.name << " ";
DeQueue(Mdancers, temp);
cout << temp.name << endl;
}
}
报数问题
报到该出列的人出队,不能出队的人先出队再入队
#include<iostream>
#include<queue>
using namespace std;
int main()
{
queue<int> Q;
int m, n, i, cnt = 1;
int number;
int flag = 1;
cin >> m >> n;
if (n >= m)
{
cout << "error!";
return 0;
}
for (i = 1; i <= m; i++)
Q.push(i);
while (!Q.empty())
{
if (cnt < n)
{
number = Q.front();
Q.pop();
Q.push(number);
cnt++;
}
else if (cnt == n)
{
if (flag == 1)
{
cout << Q.front();
flag = 0;
}
else
cout << " " << Q.front();
Q.pop();
cnt = 1;
}
}
return 0;
}
银行排队问题
先到的人先处理业务,如果到达时,窗口刚好出于空窗期,不用排队直接处理业务,没有窗口完成任务,就找到最先完成业务的窗口等待
#include<iostream>
using namespace std;
typedef struct
{
int arrive;
int deal;
}QUEUE;
int main()
{
QUEUE person[1005];
int windownum[11] = { 0 }, windowsum[11] = { 0 };
int N, K;
int i, j;
int flag;
int mintime, waittime, maxwait, index, lasttime;
double timesum;
cin >> N;
for (i = 0; i < N; i++)
{
cin >> person[i].arrive >> person[i].deal;
if (person[i].deal > 60)
person[i].deal = 60;
}
cin >> K;
timesum = maxwait = waittime = lasttime = 0;
for (i = 0; i < N; i++)
{
flag = index = 0;
mintime = 60000;
for (j = 0; j < K; j++)
{
if (windowsum[j] <= person[i].arrive)
{
windowsum[j] = person[i].arrive + person[i].deal;
windownum[j]++;
flag = 1;
break;
}
if (mintime > windowsum[j])
{
mintime = windowsum[j];
index = j;
}
}
if (flag == 0)
{
waittime = mintime - person[i].arrive;
if (maxwait < waittime)
maxwait = waittime;
timesum += waittime;
windowsum[index] = mintime + person[i].deal;
windownum[index]++;
}
}
for (i = 0; i < K; i++)
if (lasttime < windowsum[i])
lasttime = windowsum[i];
timesum = 1.0 * timesum / N;
printf("%.1f %d %d
", timesum, maxwait, lasttime);
for (i = 0; i < K; i++)
{
if (i == 0)
cout << windownum[0];
else
cout << " " << windownum[i];
}
return 0;
}
栈与队列的异同
| 相同 |
(1)都是线性结构。
(1)插入操作都是限定在表尾进行。
(3)都可以通过顺序结构和链式结构实现。
(4)插入与删除的时间复杂度都是O(1),在空间复杂度上两者也一样。
(5)多链栈和多链队列的管理模式可以相同。
| 不同 |
(1)队列先进先出,栈先进后出。
(2)删除数据元素的位置不同,栈的删除操作在表尾进行,队列的删除操作在表头进行。
(3)遍历数据速度不同。栈只能从头部取数据 也就最先放入的需要遍历整个栈最后才能取出来,而且在遍历数据的时候还得为数据开辟临时空间,保持数据在遍历前的一致性。队列不同,他基于地址指针进行遍历,而且可以从头或尾部开始遍历,但不能同时遍历,无需开辟临时空间,因为在遍历的过程中不影数据结构,速度要快的多。
(4)应用场景不同。常见栈的应用场景包括括号问题的求解,表达式的转换和求值,函数调用和递归实现,深度优先搜索遍历等;常见的队列的应用场景包括计算机系统中各种资源的管理,消息缓冲器的管理和广度优先搜索遍历等。
(5)顺序栈能够实现多栈空间共享,而顺序队列不能。
STL容器
STL有六大组件,但主要包含容器、迭代器和算法三个部分。
- 容器(Containers) :用来管理某类对象的集合。每一种容器都有其优点和缺点,所以,为了应付程序中的不同需求,STL 准备了七种基本容器类型。
- 迭代器(Iterators): 用来在一个对象集合的元素上进行遍历操作。这个对象集合或许是个容器,或许是容器的一部分。每一种容器都提供了自己的迭代器,而这些迭代器了解该种容器的内部结构。
- 算法(Algorithms):用来处理对象集合中的元素,比如 Sort,Search,Copy,Erase 那些元素。通过迭代器的协助,我们只需撰写一次算法,就可以将它应用于任意容器之上,这是因为所有容器的迭代器都提供一致的接口。
| 容器(Containers) |
- 序列式容器(Sequence containers),此为可序群集,其中每个元素均有固定位置—取决于插入时机和地点,和元素值无关。如果你以追加方式对一个群集插入六个元素,它们的排列次序将和插入次序一致。STL提供了三个序列式容器:向量(vector)、双端队列(deque)、列表(list)。
- 关联式容器(Associative containers),此为已序群集,元素位置取决于特定的排序准则以及元素值,和插入次序无关。如果你将六个元素置入这样的群集中,它们的位置取决于元素值,和插入次序无关。STL提供了四个关联式容器:集合(set)、多重集合(multiset)、映射(map)和多重映射(multimap)。
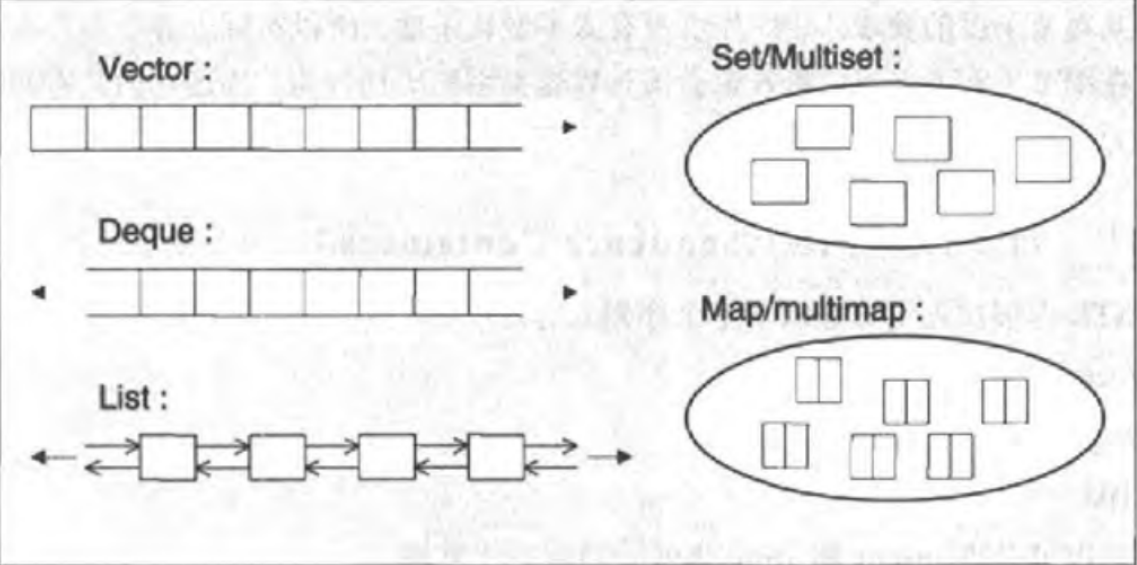
vector
它的特征是相当于可拓展的数组(动态数组),它的随机访问快,在中间插入和删除慢,但在末端插入和删除快。
创建vector对象
vector<int> v1;
vector<int> v2(10);
基本操作
v.capacity(); //容器容量
v.size(); //容器大小
v.at(int idx); //用法和[]运算符相同
v.push_back(); //尾部插入
v.pop_back(); //尾部删除
v.front(); //获取头部元素
v.back(); //获取尾部元素
v.begin(); //头元素的迭代器
v.end(); //尾部元素的迭代器
v.insert(pos,elem); //pos是vector的插入元素的位置
v.insert(pos, n, elem) //在位置pos上插入n个元素elem
v.insert(pos, begin, end);
v.erase(pos); //移除pos位置上的元素,返回下一个数据的位置
v.erase(begin, end); //移除[begin, end)区间的数据,返回下一个元素的位置
reverse(pos1, pos2); //将vector中的pos1~pos2的元素逆序存储
特点
- 拥有一段连续的内存空间,并且起始地址不变,因此它能非常好的支持随机存取,即 [] 操作符,但由于它的内存空间是连续的,所以在中间进行插入和删除会造成内存块的拷贝,另外,当该数组后的内存空间不够时,需要重新申请一块足够大的内存并进行内存的拷贝。这些都大大影响了 vector 的效率。
- 对头部和中间进行插入删除元素操作需要移动内存,如果你的元素是结构或类,那么移动的同时还会进行构造和析构操作,所以性能不高。
- 对最后元素操作最快(在后面插入删除元素最快),此时一般不需要移动内存,只有保留内存不够时才需要。
优缺点和适用场合
优点:支持随机访问,即 [] 操作和 .at(),所以查询效率高。
缺点:当向其头部或中部插入或删除元素时,为了保持原本的相对次序,插入或删除点之后的所有元素都必须移动,所以插入的效率比较低。
适用场景:适用于对象简单,变化较小,并且频繁随机访问的场景。
deque
deque(double-ended queue)是由一段一段的定量连续空间构成。一旦要在 deque 的前端和尾端增加新空间,便配置一段定量连续空间,串在整个 deque 的头端或尾端。
特点
- 按页或块来分配存储器的,每页包含固定数目的元素
- deque 是 list 和 vector 的折中方案。兼有 list 的优点,也有vector 随机线性访问效率高的优点
- 具有分段数组、索引数组, 分段数组是存储数据的,索引数组是存储每段数组的首地址
创建deque对象
deque<int> d1;
deque<int> d2(10);
基本操作
元素访问:
d[i];
d.at[i];
d.front();
d.back();
d.begin();
d.end();
添加元素:
d.push_back();
d.push_front();
d.insert(pos,elem); //pos是vector的插入元素的位置
d.insert(pos, n, elem) //在位置pos上插入n个元素elem
d.insert(pos, begin, end);
删除元素:
d.pop_back();
d.pop_front();
d.erase(pos); //移除pos位置上的元素,返回下一个数据的位置
d.erase(begin, end); //移除[begin, end)区间的数据,返回下一个元素的位置
优缺点和适用场合
优点:支持随机访问,即 [] 操作和 .at(),所以查询效率高;可在双端进行 pop,push。
缺点:不适合中间插入删除操作;占用内存多。
适用场景:适用于既要频繁随机存取,又要关心两端数据的插入与删除的场景。
list
List 由双向链表(doubly linked list)实现而成,元素也存放在堆中,每个元素都是放在一块内存中,他的内存空间可以是不连续的,通过指针来进行数据的访问,这个特点使得它的随机存取变得非常没有效率,但是由于链表的特点,它可以很有效率的支持任意地方的插入和删除操作。
特点
- 没有空间预留习惯,所以每分配一个元素都会从内存中分配,每删除一个元素都会释放它占用的内存。
- 在哪里添加删除元素性能都很高,不需要移动内存,当然也不需要对每个元素都进行构造与析构了,所以常用来做随机插入和删除操作容器。
- 访问开始和最后两个元素最快,其他元素的访问时间一样。
创建list对象
list<int> L1;
list<int> L2(10);
基本操作
元素访问:
lt.front();
lt.back();
lt.begin();
lt.end();
添加元素:
lt.push_back();
lt.push_front();
lt.insert(pos, elem);
lt.insert(pos, n , elem);
lt.insert(pos, begin, end);
lt.pop_back();
lt.pop_front();
lt.erase(begin, end);
lt.erase(elem);
sort()函数、merge()函数、splice()函数:
sort()函数就是对list中的元素进行排序;
merge()函数的功能是:将两个容器合并,合并成功后会按从小到大的顺序排列; 比如:lt1.merge(lt2); lt1容器中的元素全都合并到容器lt2中。
plice()函数的功能是:可以指定合并位置,但是不能自动排序!
优缺点和适用场合
优点:内存不连续,动态操作,可在任意位置插入或删除且效率高。
缺点:不支持随机访问。
适用场景:适用于经常进行插入和删除操作并且不经常随机访问的场景。
set和Multiset
set(集合)由红黑树实现,其内部元素依据其值自动排序,每个元素值只能出现一次,不允许重复.当 set 集合中的元素为结构体时,该结构体必须实现运算符 ‘<’ 的重载。
Multiset 和 set 相同,只不过它允许重复元素,也就是说 multiset 可包括多个数值相同的元素。
特点
- set 中的元素都是排好序的,集合中没有重复的元素;
- 如果要修改某一个元素值,必须先删除原有的元素,再插入新的元素。
- map 和 set 的插入删除效率比用其他序列容器高,因为对于关联容器来说,不需要做内存拷贝和内存移动。
创建set对象
set<T> s;
set<T, op(比较结构体)> s; //op为排序规则,默认规则是less<T>(升序排列),或者是greater<T>(降序规则)。
基本操作
s.size(); //元素的数目
s.max_size(); //可容纳的最大元素的数量
s.empty(); //判断容器是否为空
s.find(elem); //返回值是迭代器类型
s.count(elem); //elem的个数,要么是1,要么是0,multiset可以大于一
s.begin();
s.end();
s.rbegin();
s.rend();
s.insert(elem);
s.insert(pos, elem);
s.insert(begin, end);
s.erase(pos);
s.erase(begin,end);
s.erase(elem);
s.clear();//清除a中所有元素;
优缺点和适用场合
优点:使用平衡二叉树实现,便于元素查找,且保持了元素的唯一性,以及能自动排序。
缺点:每次插入值的时候,都需要调整红黑树,效率有一定影响。
适用场景:适用于经常查找一个元素是否在某群集中且需要排序的场景。
map和multmap
map 由红黑树实现,其元素都是 “键值/实值” 所形成的一个对组(key/value pairs)。每个元素有一个键,是排序准则的基础。每一个键只能出现一次,不允许重复。
map 主要用于资料一对一映射的情况,map 内部自建一颗红黑树,这颗树具有对数据自动排序的功能,所以在 map 内部所有的数据都是有序的。比如一个班级中,每个学生的学号跟他的姓名就存在着一对一映射的关系。
map为单重映射、multimap为多重映射;
map存储的是无重复键值的元素对,而multimap允许相同的键值重复出现,既一个键值可以对应多个.
特点
- 自动建立 Key - value 的对应。key 和 value 可以是任意你需要的类型。
- 根据 key 值快速查找记录,查找的复杂度基本是 O(logN),如果有 1000 个记录,二分查找最多查找 10次(1024)。
- 增加和删除节点对迭代器的影响很小,除了那个操作节点,对其他的节点都没有什么影响。
- 对于迭代器来说,可以修改实值,而不能修改 key。
- key和value一一对应的关系可以去重。
创建list对象
map<T1,T2> m;
map<T1,T2, op> m; //op为排序规则,默认规则是less<T>
基本操作
m.at(key);
m[key];
m.count(key);
m.max_size(); //求算容器最大存储量
m.size(); //容器的大小
m.begin();
m.end();
m.insert(elem);
m.insert(pos, elem);
m.insert(begin, end);
优缺点和适用场合
优点:使用平衡二叉树实现,便于元素查找,且能把一个值映射成另一个值,可以创建字典。
缺点:每次插入值的时候,都需要调整红黑树,效率有一定影响。
适用场景:适用于需要存储一个数据字典,并要求方便地根据key找value的场景。
容器配接器
除了以上七个基本容器类别,为满足特殊需求,STL还提供了一些特别的(并且预先定义好的)容器配接器,根据基本容器类别实现而成。包括:
stack
stack 容器对元素采取 LIFO(后进先出)的管理策略。
queue
queue 容器对元素采取 FIFO(先进先出)的管理策略。也就是说,它是个普通的缓冲区(buffer)。
priority_queue
priority_queue 容器中的元素可以拥有不同的优先权。所谓优先权,乃是基于程序员提供的排序准则(缺省使用 operators)而定义。Priority queue 的效果相当于这样一个 buffer:“下一元素永远是queue中优先级最高的元素”。如果同时有多个元素具备最髙优先权,则其次序无明确定义
pair类模板
主要作用是将两个数据组成一个数据,用来表示一个二元组或一个元素对,两个数据可以是同一个类型也可以是不同的类型。当需要将两个元素组合在一起时,可以选择构造pair对象。
创建pair对象
pair<int, float> p1; //调用构造函数来创建pair对象
make_pair(1,1.2); //调用make_pair()函数来创建pair对象
pair对象的使用
pair<int, float> p1(1, 1.2);
cout<< p1.first << endl;
cout<< p1.second << endl;
各容器的共性
各容器一般来说都有下列函数:默认构造函数、复制构造函数、析构函数、empty()、max_size()、size()、operator=、operator<、operator<=、operator>、operator>=、operator==、operator!=、swap()。
顺序容器和关联容器都共有下列函数:
- begin() :返回容器第一个元素的迭代器指针;
- end():返回容器最后一个元素后面一位的迭代器指针;
- rbegin():返回一个逆向迭代器指针,指向容器最后一个元素;
- rend():返回一个逆向迭代器指针,指向容器首个元素前面一位;
- clear():删除容器中的所有的元素;
- erase(it):删除迭代器指针it处元素。
各容器的时间复杂度分析器
vector 在头部和中间位置插入和删除的时间复杂度为 O(N),在尾部插入和删除的时间复杂度为 O(1),查找的时间复杂度为 O(1);
deque 在中间位置插入和删除的时间复杂度为 O(N),在头部和尾部插入和删除的时间复杂度为 O(1),查找的时间复杂度为 O(1);
list 在任意位置插入和删除的时间复杂度都为 O(1),查找的时间复杂度为 O(N);
set 和 map 都是通过红黑树实现,因此插入、删除和查找操作的时间复杂度都是 O(log N)。
| 迭代器(iterator) |
迭代器(Iterator)是一种检查容器内元素并遍历元素的数据类型。迭代器是指针的泛化,它允许程序员用相同的方式处理不同的数据结构(容器)。
迭代器类型
迭代器共分为五种,分别为: 输入迭代器(Input iterator)、输出迭代器(Output iterator)、前向迭代器(Forward iterator)、双向迭代器(Bidirectional iterator)、随机存取迭代器(Random access iterator)。
迭代器的四种定义方式
正向迭代器
容器类名::iterator 迭代器名;
常量正向迭代器
容器类名::const_iterator 迭代器名;
反向迭代器
容器类名::reverse_iterator 迭代器名;
常量反向迭代器
容器类名::const_reverse_iterator 迭代器名;
迭代器的功能
正向迭代器:假设 p 是一个正向迭代器,则 p 支持以下操作:++p,p++,*p。此外,两个正向迭代器可以互相赋值,还可以用==和!=运算符进行比较。
双向迭代器:双向迭代器具有正向迭代器的全部功能。除此之外,若 p 是一个双向迭代器,则--p和p--都是有定义的。--p使得 p 朝和++p相反的方向移动。
随机访问迭代器:随机访问迭代器具有双向迭代器的全部功能。若 p 是一个随机访问迭代器,i 是一个整型变量或常量,则 p 还支持以下操作:
- p+=i:使得 p 往后移动 i 个元素。
- p-=i:使得 p 往前移动 i 个元素。
- p+i:返回 p 后面第 i 个元素的迭代器。
- p-i:返回 p 前面第 i 个元素的迭代器。
- p[i]:返回 p 后面第 i 个元素的引用。
两个随机访问迭代器 p1、p2 还可以用 <、>、<=、>= 运算符进行比较。p1<p2的含义是:p1 经过若干次(至少一次)++操作后,就会等于 p2。其他比较方式的含义与此类似。
对于两个随机访问迭代器 p1、p2,表达式p2-p1也是有定义的,其返回值是 p2 所指向元素和 p1 所指向元素的序号之差(也可以说是 p2 和 p1 之间的元素个数减一)。
迭代器的辅助函数
使用迭代器的辅助函数需要包含头文件 algorithm。
advance(p, n):使迭代器 p 向前或向后移动 n 个元素。
distance(p, q):计算两个迭代器之间的距离,即迭代器 p 经过多少次 + + 操作后和迭代器 q 相等。如果调用时 p 已经指向 q 的后面,则这个函数会陷入死循环。
iter_swap(p, q):用于交换两个迭代器 p、q 指向的值。
迭代器用法示例
vector
#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char* argv[])
{
// Create and populate the vector
vector<int> vecTemp;
for (int i = 0; i<6; i++)
vecTemp.push_back(i);
// Display contents of vector
cout <<"Original deque: ";
vector<int>::iterator it;
for (it = vecTemp.begin(); it!=vecTemp.end(); it++)
cout <<*it <<" ";
return 0;
}
/*
输出结果:
Original deque: 0 1 2 3 4 5
*/
deque
#include <iostream>
#include <deque>
using namespace std;
int main(int argc, char* argv[])
{
// Create and populate the deque
deque<int> dequeTemp;
for (int i = 0; i<6; i++)
dequeTemp.push_back(i);
// Display contents of deque
cout <<"Original deque: ";
deque<int>::iterator it;
for (it = dequeTemp.begin(); it != dequeTemp.end(); it++)
cout <<*it <<" ";
cout <<endl;
return 0;
}
/*
输出结果:
Original deque: 0 1 2 3 4 5
*/
list
#include <iostream>
#include <list>
using namespace std;
int main(int argc, char* argv[])
{
// Create and populate the list
list<int> listTemp;
for (int i = 0; i<6; i++)
listTemp.push_back(i);
// Display contents of list
cout << "Original list: ";
list<int>::iterator it;
for (it = listTemp.begin(); it != listTemp.end(); it++)
cout << *it << " ";
cout << endl;
// Insert five 9 into the list
list<int>::iterator itStart = listTemp.begin();
listTemp.insert(itStart,5,9);
// Display the result
cout << "Result of list: ";
for (it = listTemp.begin(); it != listTemp.end(); it++)
cout << *it << " ";
cout << endl;
return 0;
}
/*
输出结果:
Original list: 0 1 2 3 4 5
Result of list: 9 9 9 9 9 0 1 2 3 4 5
*/
set
#include <iostream>
#include <set>
using namespace std;
int main(int argc, char* argv[])
{
// Create and populate the set
set<char> setTemp;
for (int i = 0; i<6; i++)
setTemp.insert('F'-i);
// Display contents of set
cout <<"Original set: ";
set<char>::iterator it;
for (it = setTemp.begin(); it != setTemp.end(); it++)
cout <<*it <<" ";
cout <<endl;
return 0;
}
/*
输出结果:
Original set: A B C D E F
*/
map
#include <iostream>
#include <map>
using namespace std;
typedef map<int, char> MyMap;
int main(int argc, char* argv[])
{
// Create and populate the map
MyMap mapTemp;
for (int i = 0; i<6; i++)
mapTemp[i] = ('F'-i);
// Display contents of map
cout <<"Original map: " <<endl;
MyMap::iterator it;
for (it = mapTemp.begin(); it != mapTemp.end(); it++)
{
cout << (*it).first << " --> ";
cout << (*it).second << std::endl;
}
cout <<endl;
return 0;
}
/*
输出结果:
Original map:
0 --> F
1 --> E
2 --> D
3 --> C
4 --> B
5 --> A
*/
1.2.谈谈你对栈和队列的认识及学习体会
- 感觉栈和队列难度很大,特别是银行排队问题还有符号配对,这真心很困难,打PTA打的特别心塞,都不会啊,而且编程量大,需要考虑的东西很多,看了很久才会懂点,好在有老师介绍的容易,通过两个头文件#include
和#include 两个头文件,接下去再进行入栈出栈入队出队操作时候会方便些,但是还是得细心些,比如top和pop的区别,一个只取栈顶不去栈顶,另一个则相反。栈是遵循“先进后出”原则,而且进出栈只能是从栈顶进行操作,队列和栈有点不一样,队列就像现实生活中的排队,从队头出队,从队尾进入,符合先进后出原则。两者都作为线性结构,有着异同点,栈和队列两者在进行插入和删除上时间复杂度都是O(1),在空间复杂度上两者也一样,插入的操作都被限制在栈顶或者队尾也就是尾部。两者不同于删除元素的位置不同,栈的删除在栈顶,队列的删除则在队头。还有应用场景的不同:栈用于括号问题还有表达式的转换和求值,深度搜索,函数的调用和递归等。而队列用于计算机系统中各种资源的管理,消息缓冲器和广度优先搜索等等..... - PTA后面几道银行排队的问题希望老师都能讲以下,真的是想了很久才很艰难的打出来,刚开始看题目的时候都看得一脸懵,写代码写的怀疑人生了真的,太难了,每次去找同学问题目的时候,都是说我要哭出来了,要绝望了,因为是真的很非常绝望啊,有的时候打着打着崩溃了就不会打了,是自己的问题,没有打好基础,想要收获是一定要付出很多的,继续加油,不能放弃...
2.PTA实验作业
2.1.题目1:7-4符号配对
2.1.1代码截图
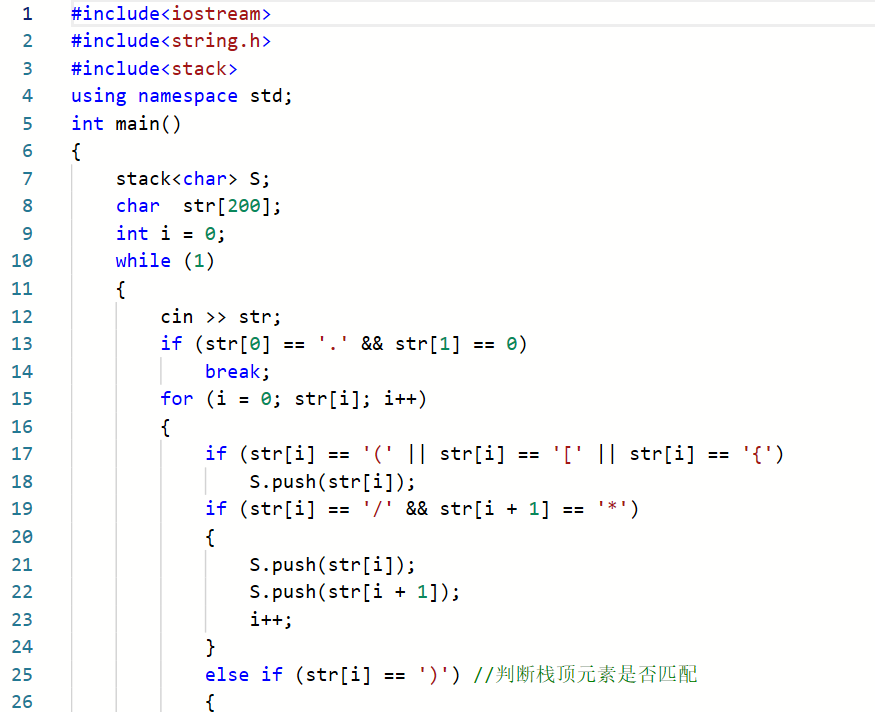





2.1.2本题PTA提交列表说明
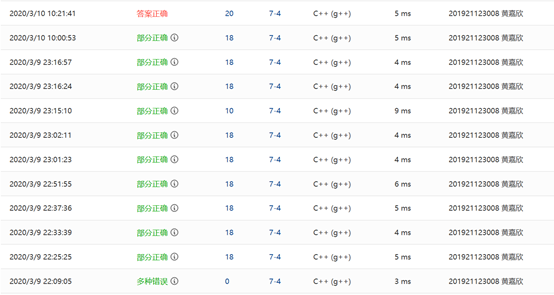
Q1:一开始有个多种错误,里面有段错误还有答案错误
A1:刚开始不会输出任何东西,检查代码的时候,忘记如果栈空的话返回的是1而栈不空返回的则是0,就用!S.empty()来判断栈空,导致了错误
Q2:样例三的匹配成功错误,把样例3复制去运行的时候摁下空格就直接输出了“YES”,没有输入结束的‘.’和换行
A2:读取整个字符串的时候,我判断是出现了‘.’就结束while循环,没有考虑到小数点也会出现’.’,样例三刚好就有小数,所以这个测试点就错了,然后我就把判断退出的条件改为了出现’.’和换行才退出
Q3:测试点3,4,5一直没过,我看匹配代码的时候一直没有什么问题,就一直在调试,也弄了很久,当时快被气的吐血了,真的很绝望...
A3:我一直在看匹配的代码,没有看整个循环结束后,有对栈空与不空的操作,然后拉到最下面的时候,才看到栈不空的时候,输出要求要输出那个“NO”,我当时的代码那里没有,导致我调试了很久出现的错误,这个真的是粗心的问题...
Q4:当出现多个不匹配的左括号,我以为是要把最开始出现的那个左括号输出,就用while循环出栈,输出第一个不匹配的左括号,可是提交的时候还是测试点没过
A4:我看我的运行结果,的确是输出了第一个左括号,一直都是不对的,然后我就去问了学长,学长就说这个是一碰到右括号,栈顶元素不匹配的时候,就是直接把栈顶元素输出的,我一口老血差点没喷在电脑上,很难受呀
Q5:18分了,就测试点4,一直卡在那里,我也不知道,这个测试点是什么意思,问了同学和学长都无果..但是我没放弃一直在造测试数据,让苍天知道我不认输
A5:最后我实在没有办法了,就去网上搜了代码,但是我看网上的代码,匹配操作和我的差不多呀,就觉得应该是一样的,然后我灵机一动,试试网上的输入代码,把测试数据,分成多个字符串输入,字符串第一个输出的为‘.’和第二个输出的是换行就退出,我改了这个输入代码去提交PTA发现过了,但是我不懂我的输入和网上的输入有什么不同,我就去问了助教,他说改了输入之后,每一行只有一个’.’和换行才会结束程序,而你的代码一行中有多个’.’和换行也是会结束程序的,这不是题目想要的,我忍住了心里的眼泪呀,猜作者的用意也太难了吧,我下次会注意看题目的........
2.2.题目2:7-5表达式转换
2.2.1代码截图

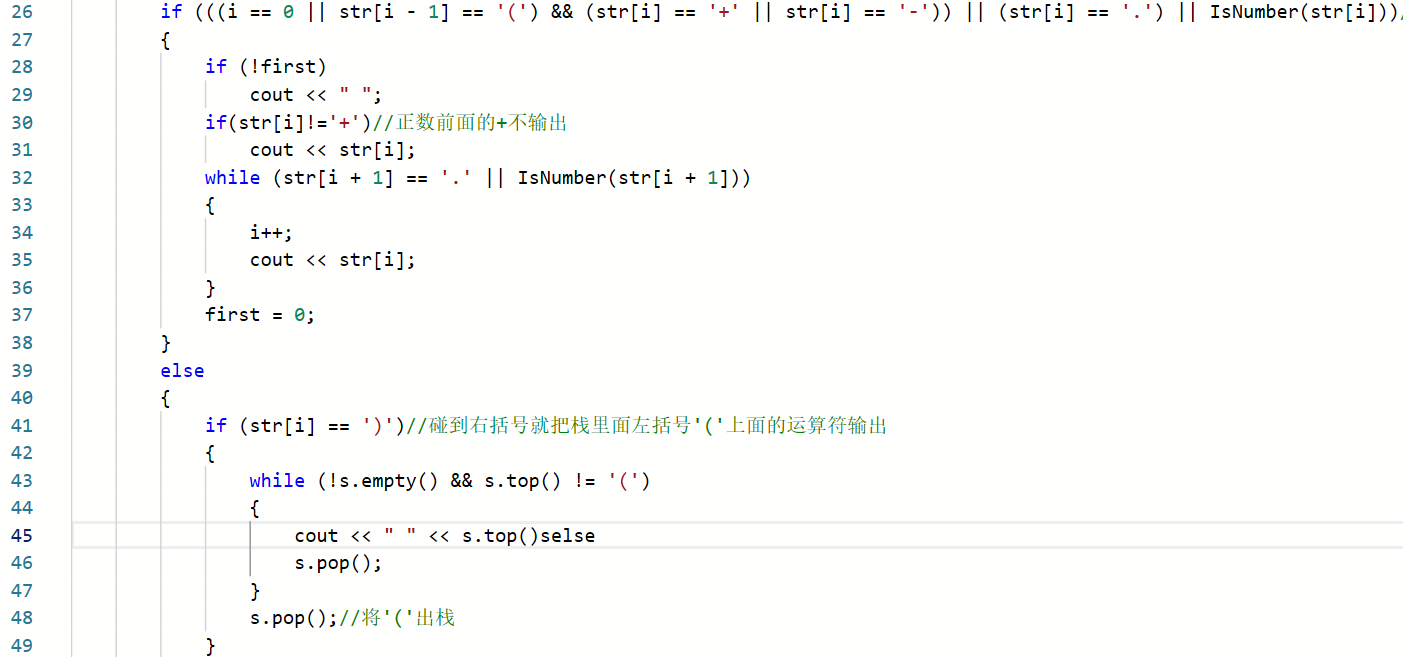


2.2.2本题PTA提交列表说明

A1:刚开始做这道题目的时候,老师就有提醒过要考虑小数和正负数的问题,然后写的时候就把各种情况都考虑出来了,就一直写写写,最后一提交就是1分
Q1:运行的时候还是发现有很多问题,小数还有正负数我都考虑到了,可是那个空格我不知道怎么处理,因为多位数的时候我的代码就是空格乱来的,然后去问了别的同学,说她在最后一个字符处输出空格,然后就是各种试,还是不行,就去问了助教,助教说第一个输出的字符就是数字,在数字那里灵活运用first就行,我就去改正了自己的代码,空格问题解决了
A2:当一个数字是大于10的负数或者是小数时,就会输出很多个空格,导致了答案错误
Q2:刚开始是定义了一个队列,把数字存到队列里面,再将队列输出,可是这样错误更多了,是我自己把问题复杂化,后面考虑到其实可以直接运用for循环里面嵌套一个while循环把数字后面是数字或者小数点的数字继续输出,并且让i++自增,让下标移动到要进行判断的下一个字符
A3:正负数那个测试点一直没过,然后我去问了过了这道题目的同学,她说正数有可能前面会有‘+’号,但是这个‘+’号是不可以输出的
Q3:改代码呀改代码,越改越错的代码,头都要秃噜皮了,想到是如果当前字符为‘+’,就让i自增,可是外层循环i会自增会跳过一个字符,后来就是想到在数字的条件判断中,加一个条件判断,当前字符不为‘+’号则输出
A4:当时写代码的时候正负数的判断是,前面’+’或‘-’号的前面是‘(’,测试点三也就卡在那里没过了,我以为题目要求我们负数要带括号输出,然后就改代码了
Q4:带括号输出,错误点更多了,说明还是不用带括号输出,想起上个学期我们做过一道题目,带符号的数可能出现在第一个,但是第一个数是没有括号括起来的,就把判断为数字的条件改了一下才过了,唉,绝望啊,终于知道自己的发际线是怎么往后移的了
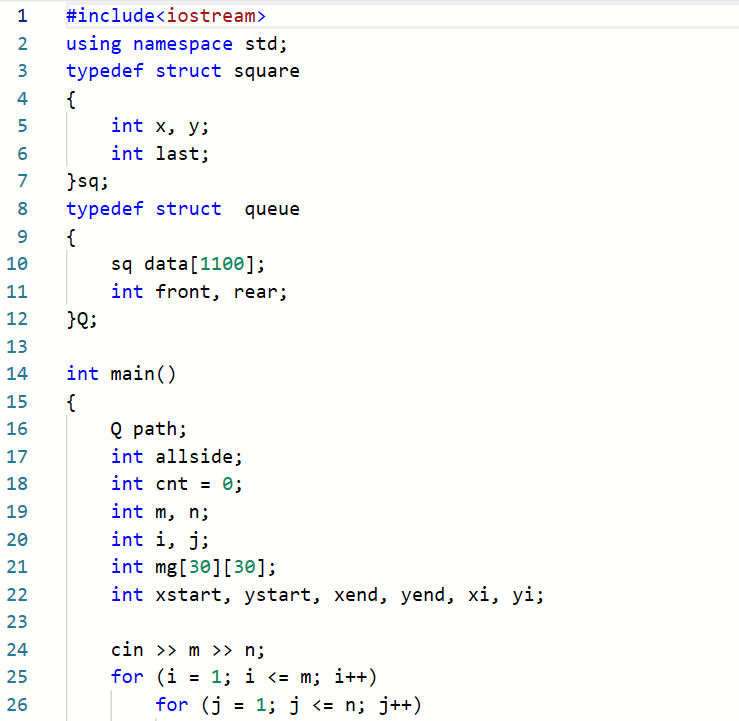
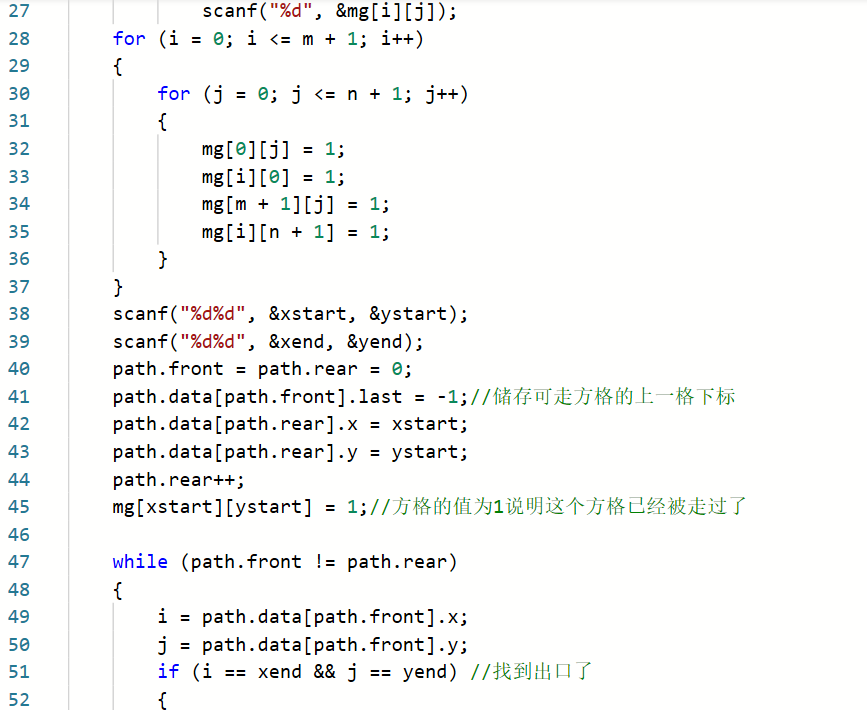
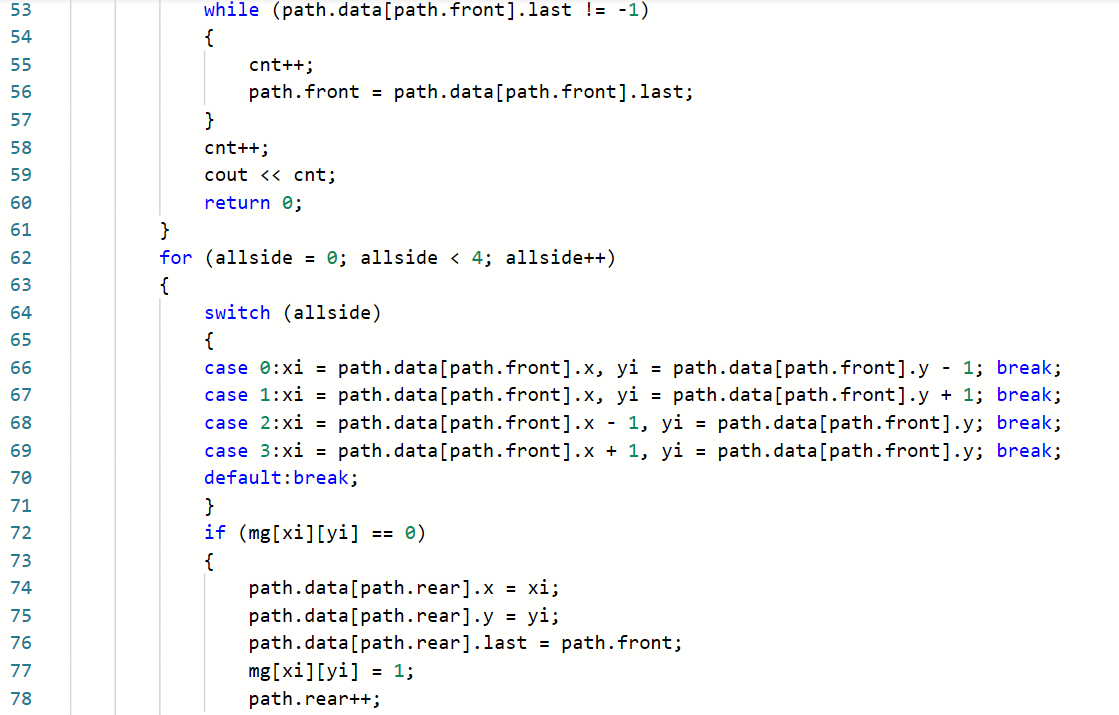
2.3.题目2:7-8 电路布线
2.3.1代码截图

2.3.2本题PTA提交列表说明

Q1:看着题目知道是迷宫问题,然后就去看了看老师那个迷宫的代码,就去写的代码,但是一直运行不了就想着提交以下看下是哪里错了,结果一直都是运行超时
A1:因为这道题目是要找到最短路径,和老师那个代码的功能不是一样的,但是我又是毫无头绪就去问了别的同学,他说要用队列要写,遇到不同的可走方位就会分出好几个队列来走,同时要记录每条路线的上一个方位,最先到达终点位置的那条队列,就是最短路径
Q2:根据同学给我讲解的具体思路,我就去改了我的代码,可是一直都是段错误,会死循环
A2:后面发现我的while循环,用的是恒真,我以为这种题目一定会找到出口就用的恒真条件,可是我后面的代码也是有问题的,所以这个条件不能这样用
Q3:把前面提到的问题都改了之后,可以输出了,但是我把样例输进去之后,会输出空白
A3:一直在阅读代码找错,发现是switch那里,xi和yi赋值的那里我用了‘,’隔开,太久没用switch了就忘记了怎么用了,把‘,’号改成‘;’了
Q4:把样例输进去的时候,可以输出cnt了,可是输出不是正确答案,输出的是23
A4:因为我找了很久没看到错误,然后就去问了同学,他说cnt不能在可以走的那个地方就自增计算格数,要先找到最先到达终点的那条线路就是最短线路,然后根据每条路线的last从终点反推到起点,这个时候计算走过的格子的个数,在输出就可以了,然后我就根据这个思路改过了代码
Q5:改完后的代码可以输出,但是输出的结果是15,比正确结果少了一个格数
A5:检查代码的时候发现是自己在那个计算格数的while循环处,退出循环后要增加1,这条语句漏掉了,加入这条语句就对了
3.阅读代码
3.1 题目及解题代码——水壶问题

using PII = pair<int, int>;
class Solution {
public:
bool canMeasureWater(int x, int y, int z) {
stack<PII> stk;
stk.emplace(0, 0);
auto hash_function = [](const PII& o) {return hash<int>()(o.first) ^ hash<int>()(o.second);};
unordered_set<PII, decltype(hash_function)> seen(0, hash_function);
while (!stk.empty()) {
if (seen.count(stk.top())) {
stk.pop();
continue;
}
seen.emplace(stk.top());
auto [remain_x, remain_y] = stk.top();
stk.pop();
if (remain_x == z || remain_y == z || remain_x + remain_y == z) {
return true;
}
// 把 X 壶灌满。
stk.emplace(x, remain_y);
// 把 Y 壶灌满。
stk.emplace(remain_x, y);
// 把 X 壶倒空。
stk.emplace(0, remain_y);
// 把 Y 壶倒空。
stk.emplace(remain_x, 0);
// 把 X 壶的水灌进 Y 壶,直至灌满或倒空。
stk.emplace(remain_x - min(remain_x, y - remain_y), remain_y + min(remain_x, y - remain_y));
// 把 Y 壶的水灌进 X 壶,直至灌满或倒空。
stk.emplace(remain_x + min(remain_y, x - remain_x), remain_y - min(remain_y, x - remain_x));
}
return false;
}
};
3.1.1 该题的设计思路
观察题目可知,在任意一个时刻,此问题的状态可以由两个数字决定:X 壶中的水量,以及 Y 壶中的水量。
在任意一个时刻,我们可以且仅可以采取以下几种操作:
把 X 壶的水灌进 Y 壶,直至灌满或倒空;
把 Y 壶的水灌进 X 壶,直至灌满或倒空;
把 X 壶灌满;
把 Y 壶灌满;
把 X 壶倒空;
把 Y 壶倒空。
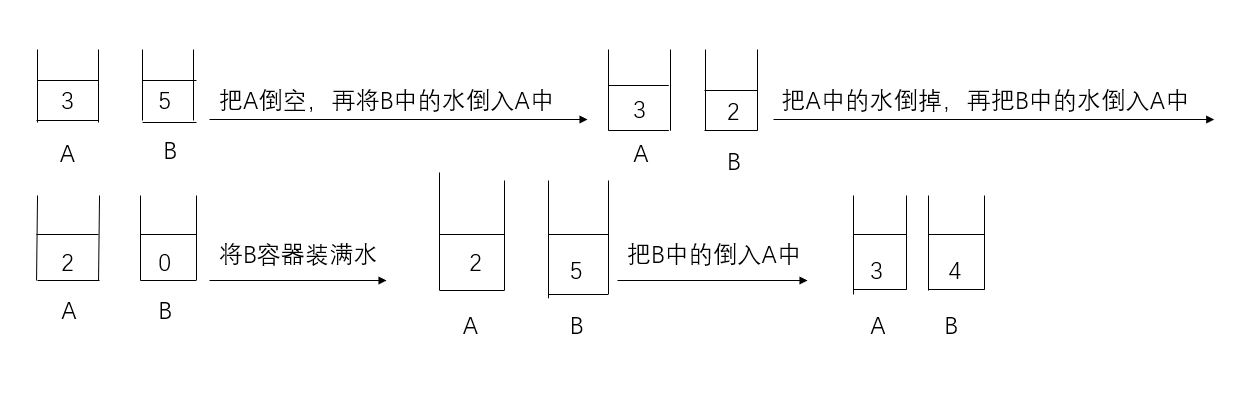
时间复杂度O(xy)
空间复杂度O(xy)
3.1.2 该题的伪代码
定义一个pair的数据结构seen存储所有已经搜索过的 remain_x, remain_y 状态,把与当前top相同的(x,y)给排除掉
while (!stk.empty()) do
if (seen.count(stk.top()))
stk出栈
continue
end if
将栈顶元素放入,seen中,储存已经搜索过的状态
记录水壶A和B的剩余量remain_x和remain_y为stk栈顶元素
if (X剩余为Z || Y剩余为Z || X剩余与Y剩余之和为Z)
返回真
end if
把 X 壶灌满,stk.emplace(x, remain_y)
把 Y 壶灌满,stk.emplace(remain_x, y)
把 X 壶倒空,stk.emplace(0, remain_y)
把 Y 壶倒空,stk.emplace(remain_x, 0)
把 X 壶的水灌进 Y 壶,直至灌满或倒空,stk.emplace(remain_x - min(remain_x, y - remain_y), remain_y + min(remain_x, y - remain_y))
把 Y 壶的水灌进 X 壶,直至灌满或倒空,stk.emplace(remain_x + min(remain_y, x - remain_x), remain_y - min(remain_y, x - remain_x))
end
返回假
3.1.3 运行结果
3.1.4分析该题目解题优势及难点。
- 优势:
本题可以使用深度优先搜索来解决。搜索中的每一步以 remain_x, remain_y 作为状态,即表示 X 壶和 Y 壶中的水量。在每一步搜索时,依次尝试所有的操作,递归地搜索下去。这可能会导致陷入无止境的递归,因此使用一个哈希结合(HashSet)存储所有已经搜索过的 remain_x, remain_y 状态,保证每个状态至多只被搜索一次。 - 难点:
这道题目外界的水是无限的,可以随时给A,B两个容器加满水,也可以随时将A,B容器的水倒掉,或者将B中的水往A倒满,A中往B中倒满,因此只需要找到x,y的最大公约数并判断z是否是它的倍数即可,只要突破这个线索就可以找到解题的关键,这就是题目的难点
3.2 题目及解题代码——有序队列

解题代码
char * orderlyQueue(char * S, int K)
{
int len = strlen(S);
char *ret = (char*)malloc(sizeof(char)*(strlen(S)+1));
strcpy(ret, S);
if (K == 1 && strlen(S) > 0)
{
char *cur = (char*)malloc(sizeof(char)*(strlen(S)+1));
strcpy(cur, &S[1]);
cur[len-1] = S[0];
cur[len] = 0;
while (strcmp(cur, S))
{
if (strcmp(cur, ret) < 0) strcpy(ret, cur);
char c = cur[0];
for (int i=0; i<len; i++) cur[i] = cur[i+1];
cur[len-1] = c;
}
free(cur);
}
else
{
int *hash = (int*)malloc(sizeof(int)*26);
memset(hash, 0, sizeof(int)*26);
for (int i=0; i<len; i++) hash[S[i]-'a']++;
int p = 0;
for (int i=0; i<26; i++) {
for (int j=0; j<hash[i]; j++) ret[p++] = i+'a';
}
ret[p] = 0;
free(hash);
}
return ret;
}
3.2.1 该题的设计思路
当K>1时:
利用一层循环统计每一个小写字母的个数
两层循环,外循环为二十六的小写字母,内层循环是字母的个数,按照从0开始输出的顺序
当K=1时
暴力解法,将第一个字符移到队尾形成一个新的队列,再将新队列和旧队列进行strcmp(new,S)比较,如果是小于,old=new,new在按照之前的方式形成新的队列

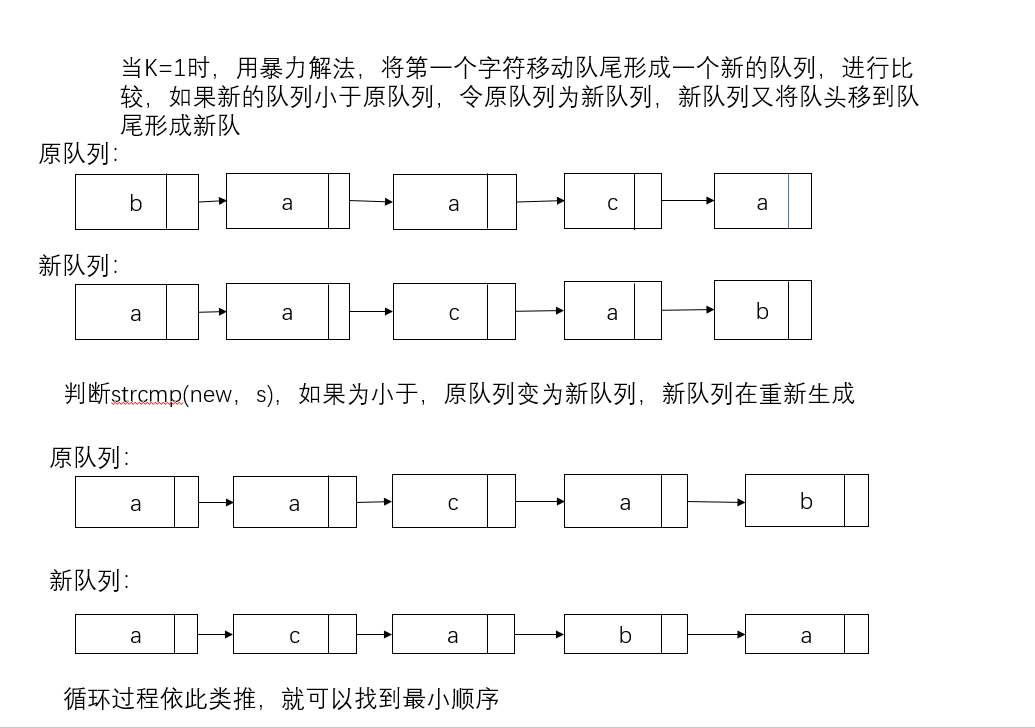
时间复杂度O(n)
空间复杂度O(n)
3.2.2 该题的伪代码
定义整型变量len = strlen(S)记录数组长度
定义字符串ret[MAXSIZE]
定义字符串cur[MAXSIZE]
定义数组hash[MAXSIZE]存放字母个数
将S字符串复制到ret中
if(k为1并且字符串长度大于0)
将字符串第一个元素移到队尾形成一个新的字符串放在cur中
while(strcmp(cur,S))
if(strcmp(cur,ret)<0)
将cur字符串复制到ret中
end if
将cur第一个元素移到队尾形成一个新的cur
end
else
for int i=0 to len do i++
将字母转成下标存进hash数组中
int p=0;
for int i=0 to 26 do i++
for int j=0 to hash[i] do j++
ret[p++]=i+'a' //ret[]数组就是新的最小顺序的可输出数组
end if
3.2.3 运行结果

3.2.4分析该题目解题优势及难点。
- 优势:
如果没有不能理解这个题目的话,会绕很多弯子,就是无从下手的感觉,我当时看代码的时候还没看懂为什么要分K>1和K=1的情况,看完之后就是这解题思路秒啊,我理解了题目的意思之后想到的解法就是将利用我们上个学期学习的排序方法将整个队列重排序,但是整个算法的时间复杂度就是O(lenth·lenth),我现在看见嵌套循环就害怕了呀,我经常PTA的测试点卡在大数据段错误,所以这种能降低时间复杂度的算法都是好算法,更何况解题代码直接降到了O(lenth),从平方降到一次方的代码是值得我们好好研究的,这个学期开学的时候,林老师就说如果能把一个算法的时间复杂度从O(N·N)降到O(NlogN)都是很了不起的。解题代码的思路在K=1的处理上就很巧妙,虽说是暴力解法可是它的复杂度并不高,刚开始还不能理解为什么这样的循环一定会找到最低,后面自己手动写写过程就能理解了。现在我才是真正的懂得了老师让我们写博客作业的苦心所在,第一大题让我们复习(温故而知新),第二大题让我们纠错,从错误中找到方法,第三大题让我们阅读优秀代码,学习优秀代码,就是想让我们学习优秀码农的思维,好的算法就是好的思维,思维是真的很重要,因为学到现在,我们不仅仅是会写代码,而是第一时间想到最快最好的代码。 - 难点:
这道题目的难点就是理解题目了,很像是在做数学题目了,代码的实现可能并不是很困难,如果这道题目把字符串的范围扩大到10000,大部分的代码就是要卡运行超时了,而且我看了上面大部分的解题代码,时间复杂度不是O(lenth·lenth)就是O(NlogN),算法的优化也算是这道题目的难点之一了