机器学习实战---使用FP-growth算法来高效发现频繁项集

一：参考资料

（一）机器学习实战

（二）以下3篇简单了解

https://baijiahao.baidu.com/s?id=1661651339862291744&wfr=spider&for=pc（不全，但简单）

https://blog.csdn.net/qq_40587575/article/details/79997195（稍微看看）

https://blog.csdn.net/qq1010885678/article/details/45244829（排版还可以）

（三）下面PPT不错（可以完全理解，且案例丰富）

https://wenku.baidu.com/view/5a28e351bed126fff705cc1755270722182e594b.html（下面两则案例来自此处）

二：案例一（FP-growth算法原理）

 

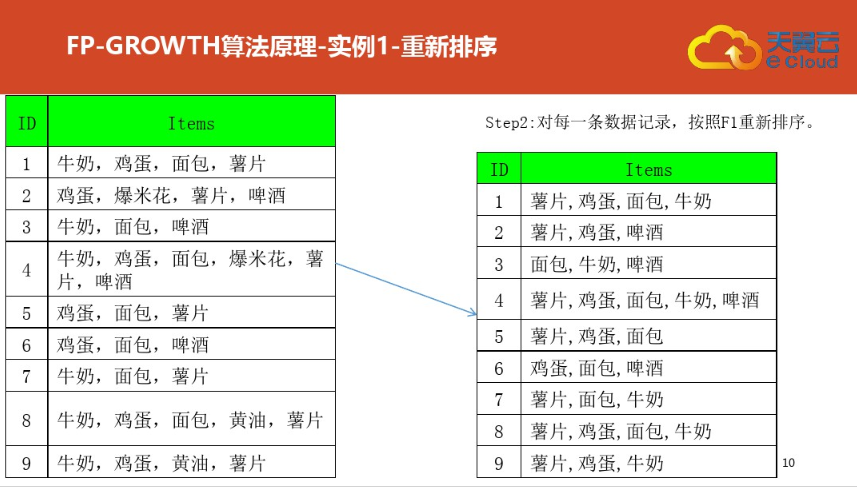
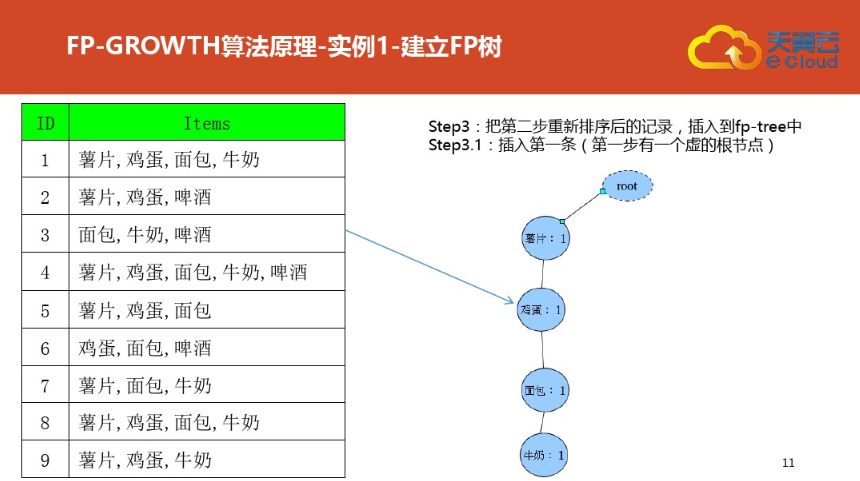
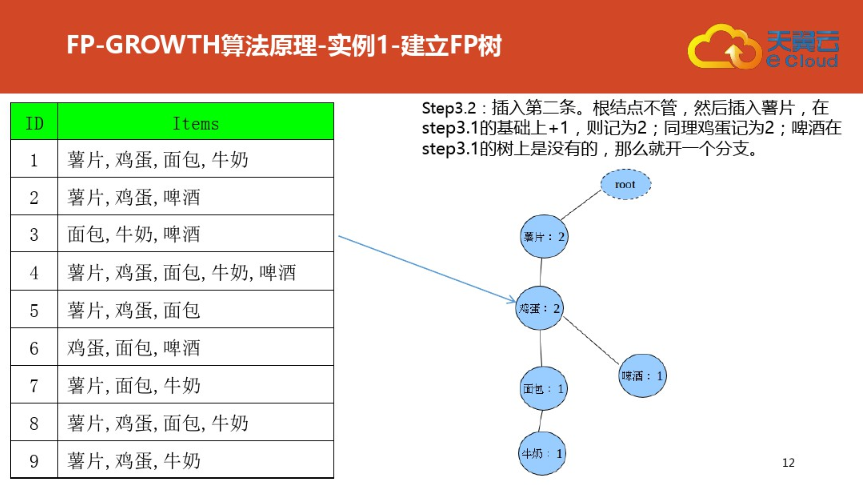
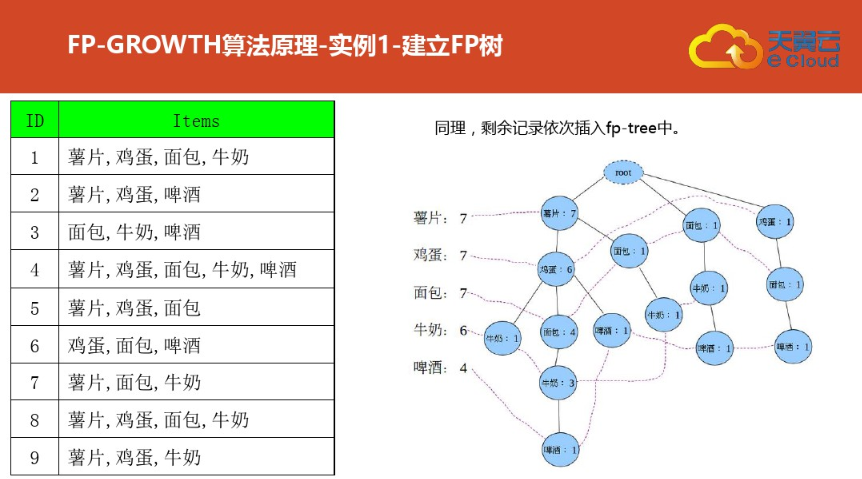
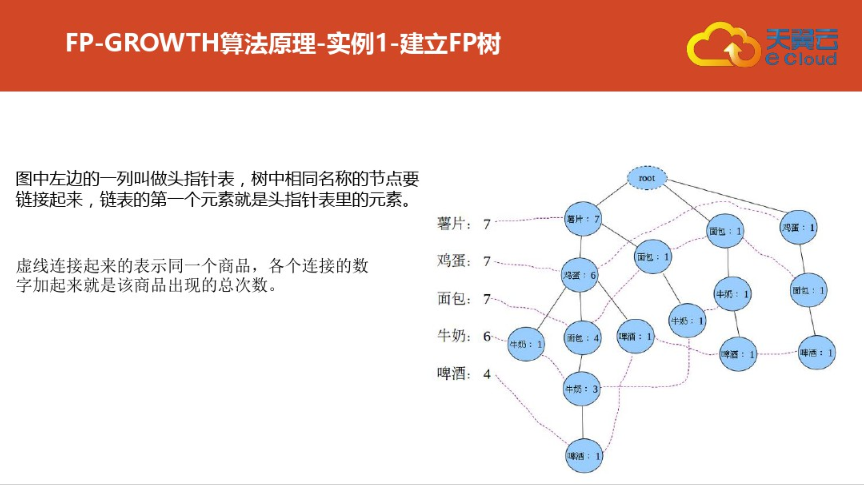
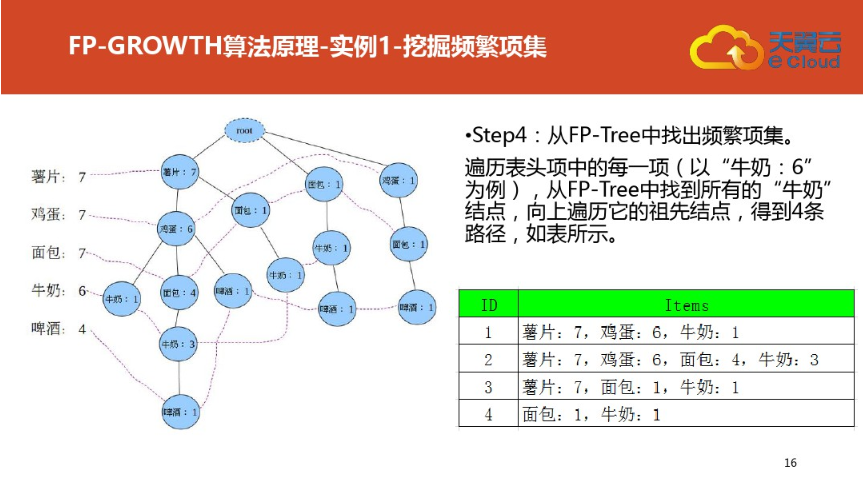
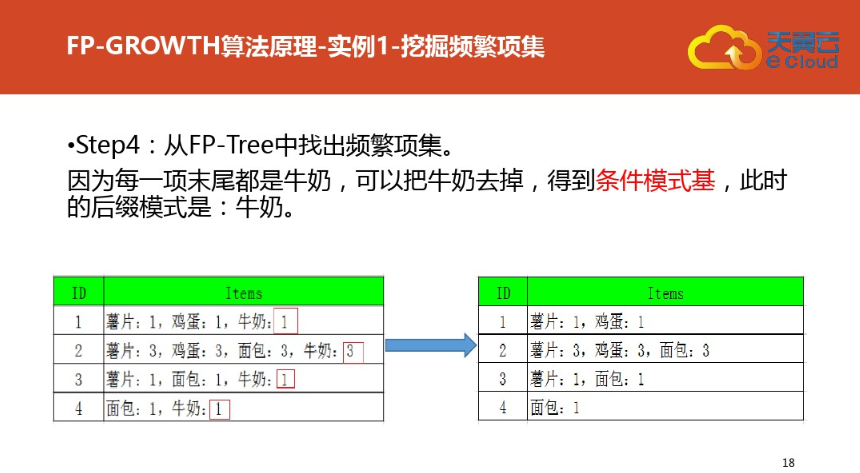
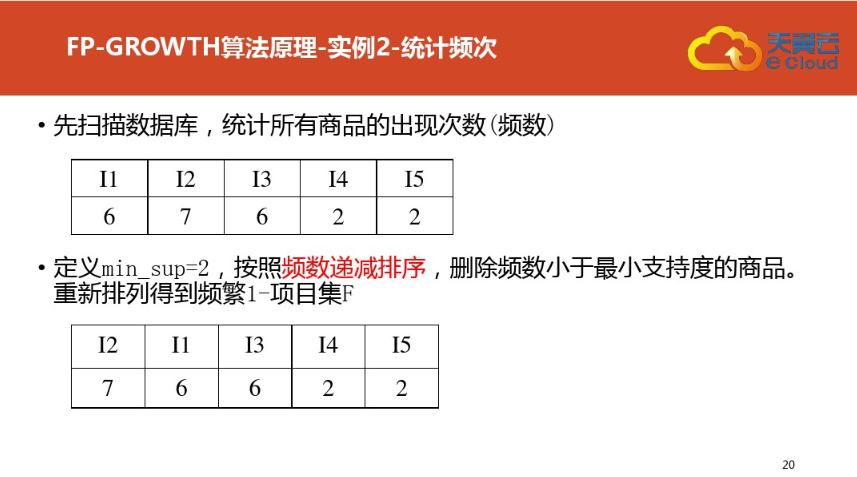
三：案例二（更详细）尤其是频繁集挖掘

 

 

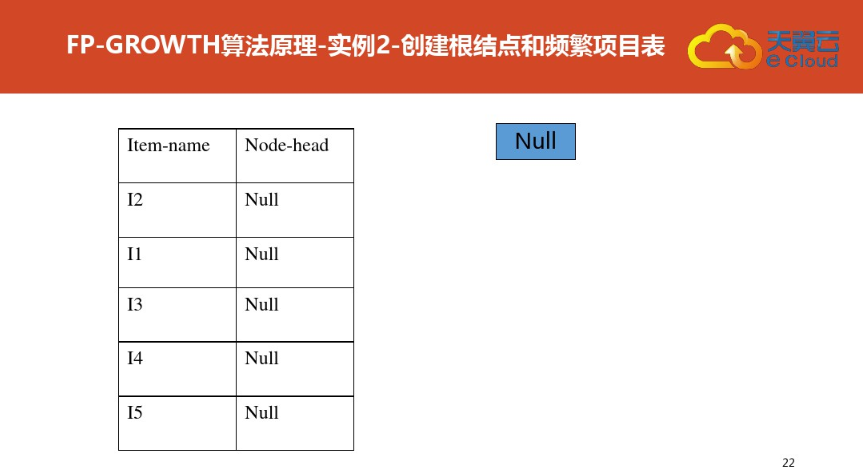
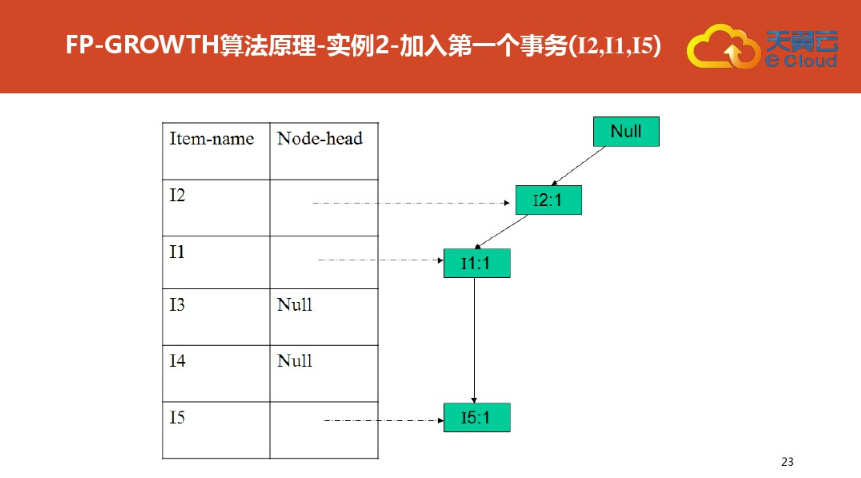
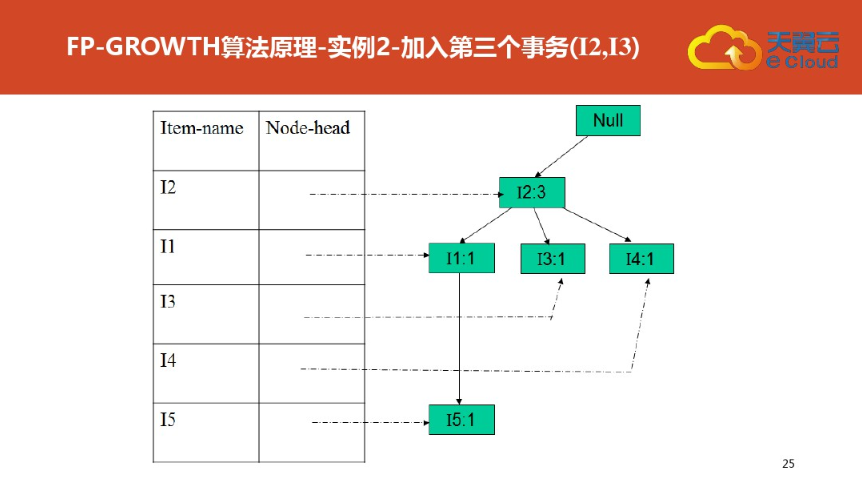
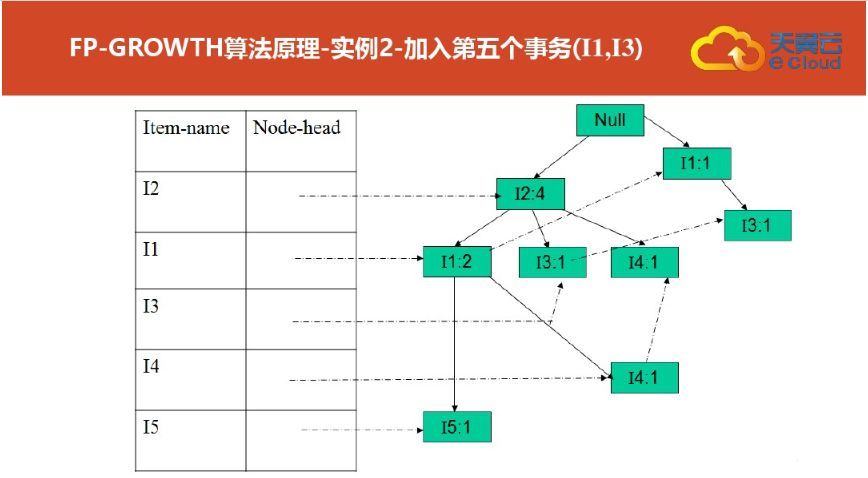
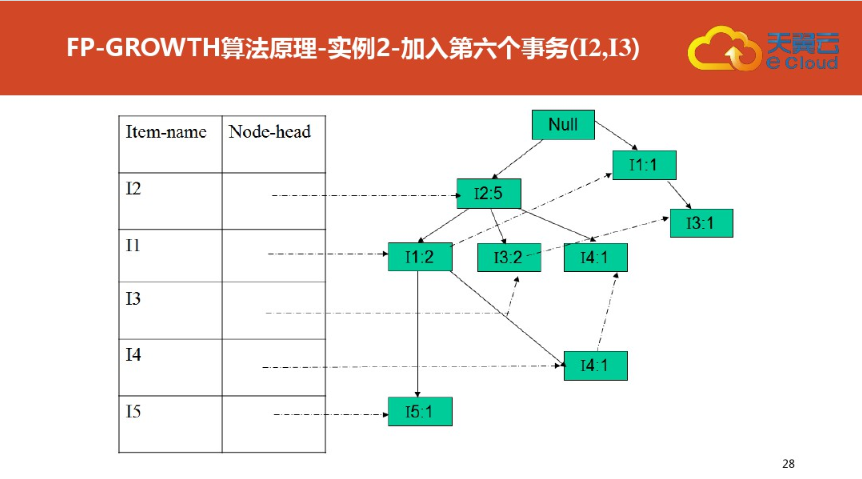
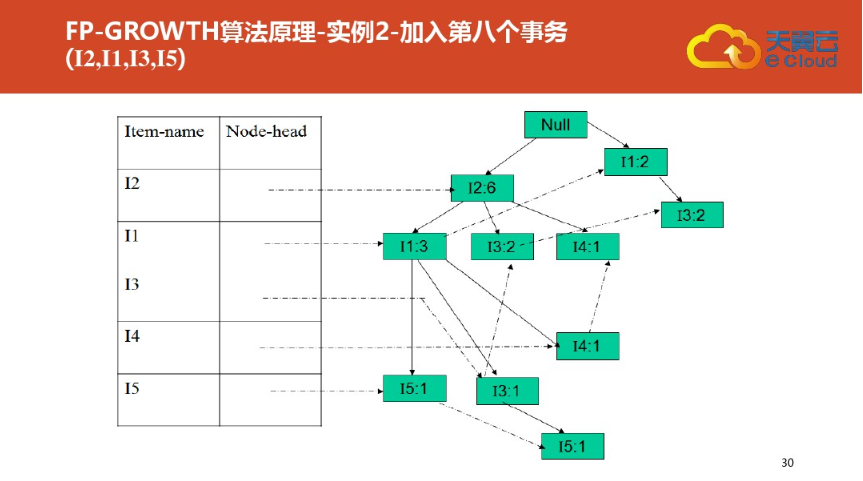
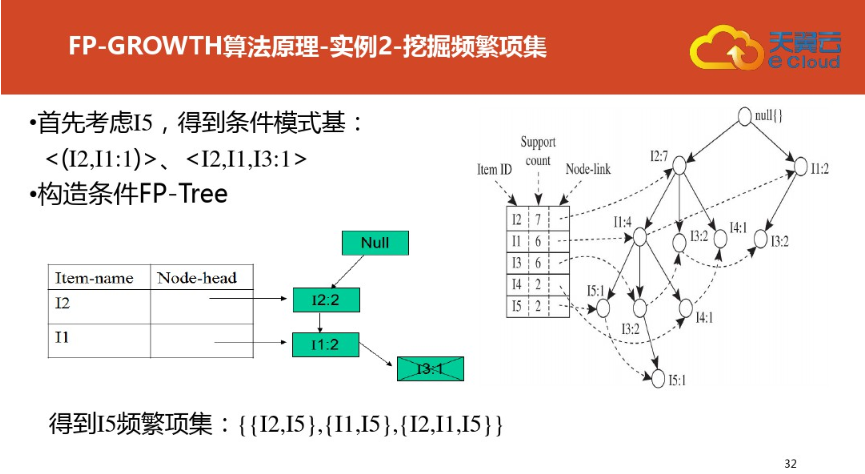
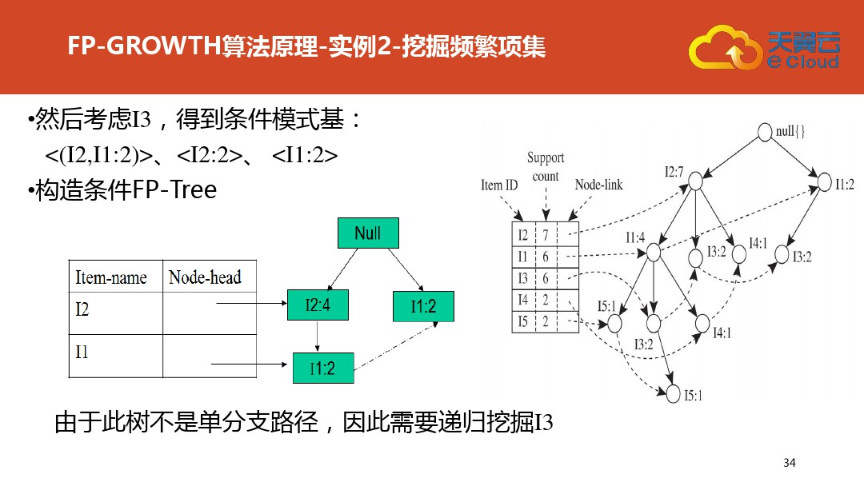
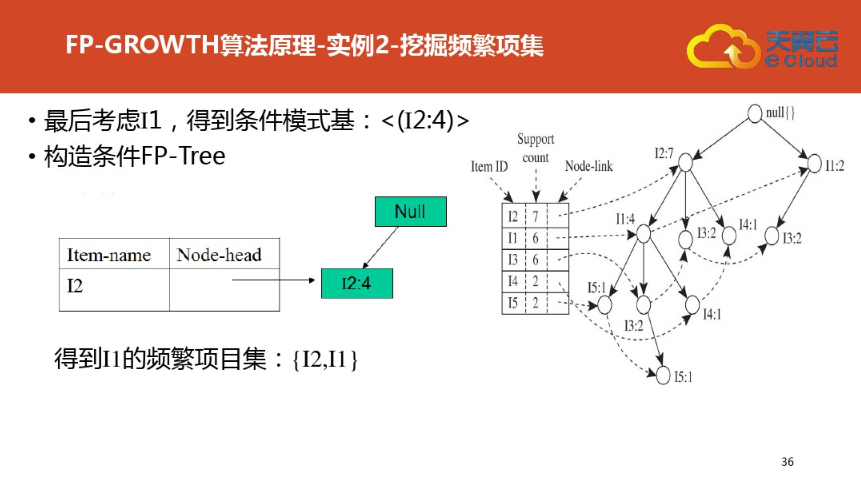
四：FP树结构定义

#一：FP树结构定义
class treeNode:
    def __init__(self,nameValue,nameOccur,parentNode):  #nameValue节点名称，nameOccur计数，parentNode指向父节点
        self.name = nameValue   #节点名称
        self.count = nameOccur  #计数器
        self.nodeLink = None    #用来存放节点信息，用来指向下一个同类（同名称）的节点
        self.parent = parentNode    #指向父节点
        self.children = {}  #子节点使用字典进行存放

    def inc(self,numOccur):
        self.count += numOccur

五：数据加载

#二：加载数据
def loadSimDat():
    simpDat = [["r","z","h","j","p"],
               ["z","y","x","w","v","u","t","s"],
               ["z"],
               ["r","x","n","o","s"],
               ["y","r","x","z","q","t","p"],
               ["y","z","x","e","q","s","t","m"],
               ]
    return simpDat

def createInitSet(dataSet): #对数据进行处理，获取我们要求的数据集格式
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1

    #返回字典类型{frozenset({'j', 'h', 'z', 'r', 'p'}): 1, frozenset({'y', 'v', 'x', 'w', 'u', 's', 't', 'z'}): 1...}
    return retDict

六：根据createInitSet方法得到的数据集类型，创建FP树 和 FP条件树

#三：根据createInitSet方法得到的数据集类型，创建FP树 和 FP条件树
#1.建树主函数
def createTree(dataSet,minSup=1):
    headerTable = {}    #存放头指针表
    for trans in dataSet:   #遍历数据,注意我们使用dataSet.items()可以遍历(key,val)对，直接遍历dataSet是对key的操作
        for item in trans:  #item是frozenset类型
            headerTable[item] = headerTable.get(item,0) + dataSet[trans]    #计数操作，其中dataSet[trans]返回字典对于values

    #重点：进行初次剪枝，去掉那些单个元素支持度太低的数据元素
    keys = list(headerTable.keys())
    for k in keys:
        if headerTable[k] < minSup:
            del(headerTable[k]) #达到剪枝效果

    #检查剪枝后是否还有数据存在
    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0:
        return None,None    #因为我们在正常情况下，返回的数据是FP树和头指针表

    #修改头指针表的格式，使得可以指向同类节点（实现链表操作）
    for k in headerTable:
        headerTable[k] = [headerTable[k],None]  #多出的None用来保存后面需要的节点信息

    #先产生根节点
    retTree = treeNode("Null Set",1,None)   #节点名称，出现次数，父节点

    #开始建树
    for tranSet,count in dataSet.items():
        localD = {} #用来保存本样本frozenset({'j', 'h', 'z', 'r', 'p'}): 1的keys是否是频繁项集
        for item in tranSet:
            if item in freqItemSet: #是在频繁项集中
                localD[item] = headerTable[item][0] #添加到localD保存次数
        if len(localD) > 0: #如果在本次样本中有数据在频繁项集中，则开始进行更新树---重点
            #对我们得到的临时localD频繁项集进行排序，将在更新树按照出现最高顺序进行更新（例如最大堆，但不是）
            orderItems = [v[0] for v in sorted(localD.items(),key=lambda p:p[1],reverse=True)]  #大到小排序
            updateTree(orderItems,retTree,headerTable,count)

    return retTree,headerTable  #返回我们需要的树和头指针表

#2.按照传入的一个样本frozenset({'j', 'h', 'z', 'r', 'p'})《注意：是排序好的，大到小》，对树进行更新
def updateTree(items,inTree,headerTable,count):
    """
    重点：我们使用递归方法建树
    :param items: 是传入的排序好的样本frozenset({'j', 'h', 'z', 'r', 'p'})
    :param inTree: 是我们要建立的树
    :param headerTable: 是我们要对头指针表进行修改节点指向，
    :param count: 是本样本在数据集中出现的次数
    """
    if items[0] in inTree.children: #已经存在该增加计数
        inTree.children[items[0]].inc(count)    #增加计数
    else:   #开始进行新增节点
        inTree.children[items[0]] = treeNode(items[0],count,inTree)  #节点按照特定的数据结构修改
        #由于我们有新增的节点，所以我们需要更新头指针表中的nodeLink链表信息，达到链表将同类型的节点链接
        if headerTable[items[0]][1] == None:    #原本不存在，则直接添加
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:   #找到同类节点的链路中的末尾，进行添加
            updateHeader(headerTable[items[0]][1],inTree.children[items[0]])    #更新头指针表

    #注意：由于我们的样本中有多个排序好的数据，所以，我们需要递归更新下面的数据
    if len(items) > 1:
        updateTree(items[1::],inTree.children[items[0]],headerTable,count)

#3.更新头指针表
def updateHeader(headerNode,newNode):
    while headerNode.nodeLink != None:
        headerNode = headerNode.nodeLink
    headerNode.nodeLink = newNode

七：开始从上面获取的FP树中，获取各个数据的条件模式基

#四：开始从上面获取的FP树中，获取各个数据的条件模式基
#1.从FP树种获取头指针表中的各个数据的条件模式基（即找前缀路径，设置计数为当前节点计数值）
def findPrefixPath(treeNode):   #书本上多了一个参数？？这里直接传我们指定的节点，查找前缀路径
    condPats = {}
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode,prefixPath) #获取前缀路径
        #保存前缀路径，和计数值
        if len(prefixPath) > 1: #保证除了本身节点之外，还存在其他前缀
            condPats[frozenset(prefixPath[1:])] = treeNode.count    #注意：使用frozenset类型作为key,并且保存时不含有本身节点
        treeNode = treeNode.nodeLink    #遍历下一个同类型节点

    return condPats #返回所有的前缀路径

#2.向上递归遍历树，找前缀节点信息
def ascendTree(treeNode,prefixPath):    #将结果保存在prefixPath中
    while treeNode.parent != None:  #除了根节点（无用）之外，都进行添加节点
        prefixPath.append(treeNode.name)
        treeNode = treeNode.parent

八：开始查找频繁集（注意：上面只对单个数据进行了一次支持度裁剪，下面会对各个组合进行裁剪）

#五：开始查找频繁集（注意：上面只对单个数据进行了一次支持度裁剪，下面会对各个组合进行裁剪）
#根据条件基模型来构建条件FP树
def mineTree(headerTable,minSup,preFix,freqItemList):
    """
    :param headerTable: 是我们生成FP树时，生成的头指针表
    :param minSup: 最小支持度，用来对复合的数据进行筛选
    :param preFix: 首次为空集合，用来保存当前前缀
    :param freqItemList: 首次为空列表，用来保存所有的频繁项集
    """
    #对头指针表中的元素按照支持度（出现频率）从小到大排序
    bigL = [v[0] for v in sorted(headerTable.items(),key=lambda p:p[1][0])]
    #从满足最小支持度的头指针表的最小元素开始，遍历头指针表，挖掘频繁数据项
    for basePat in bigL:    #最好只思考一次循环数据
        #保存当前前缀路径
        newFreqSet = preFix.copy()
        #将当前频繁元素加入频繁集合中（这里就是将头指针表元素加入---已经是满足的）
        newFreqSet.add(basePat) #都是frozenset类型---------注意：
        #1.newFreqSet.add(basePat)这一步我们可以看案例I5推导，这里先加入I5，再获取条件FP树，
        #之后根据HeaderTable判断是否为None
        #由案例可知，返回非None,
        #2.对headerTable中I2 I1建树，newFreqSet中含有I5，再分别加上I1，I2
        #2.1先加上I1，即得到I1 I5
        #之后根据HeaderTable判断是否为None
        #由案例可知，返回非None,
        #2.1.1对headerTable中I2建树，newFreqSet中含有I1 I5，再加上I2 即可得到I2 I1 I5
        #2.2再在I5基础上，加上I2，即可得到I2 I5
        #之后根据HeaderTable判断是否为None
        #由案例可知，返回None,退出
        #得到I2 I5， I1 I5，    I2 I1 I5

        #将每个频繁元素添加到频繁项集列表中
        freqItemList.append(newFreqSet)
        #将每个频繁项，都调用findPrefixPath函数，找到前缀路径
        condPattBases = findPrefixPath(headerTable[basePat][1])
        #重点：根据当前元素项生成的前缀路径和最小支持度，生成条件FP树（内部会增加计数值）
        myCondTree,myHead = createTree(condPattBases,minSup)    #从这里可以看出，我们要保存原始数据和前缀路径发现函数返回相同数据类型
        #如果条件FP树中有元素项，则可以再次递归生成条件树
        if myHead != None:  #所以对于我们新的myHead必须在使用条件模型基时，满足最小支持度
            #递归挖掘该条件树，每次向上推一个节点（条件模型基都不包含本节点，所以一直在向上走）
            mineTree(myHead,minSup,newFreqSet,freqItemList)

九：结果测试

dataSet = createInitSet(loadSimDat())
tree,headertable = createTree(dataSet,3)    #注意：因为我们建树的时候，支持度相同的节点不止一个，比如t:3,s:3，所以建树结果顺序可能不同
freqItemList = []
mineTree(headertable,3,set([]),freqItemList)
print(freqItemList)

[{'r'}, {'s'}, {'x', 's'}, {'y'}, {'z', 'y'}, {'x', 'y'}, {'z', 'x', 'y'}, {'t'}, {'z', 't'}, {'x', 't'}, {'z', 'x', 't'}, {'y', 't'}, {'z', 'y', 't'}, {'y', 't', 'x'}, {'z', 'y', 't', 'x'}, {'x'}, {'z', 'x'}, {'z'}]

全部代码：

#一：FP树结构定义
class treeNode:
    def __init__(self,nameValue,nameOccur,parentNode):  #nameValue节点名称，nameOccur计数，parentNode指向父节点
        self.name = nameValue   #节点名称
        self.count = nameOccur  #计数器
        self.nodeLink = None    #用来存放节点信息，用来指向下一个同类（同名称）的节点
        self.parent = parentNode    #指向父节点
        self.children = {}  #子节点使用字典进行存放

    def inc(self,numOccur):
        self.count += numOccur

#二：加载数据
def loadSimDat():
    simpDat = [["r","z","h","j","p"],
               ["z","y","x","w","v","u","t","s"],
               ["z"],
               ["r","x","n","o","s"],
               ["y","r","x","z","q","t","p"],
               ["y","z","x","e","q","s","t","m"],
               ]
    return simpDat

def createInitSet(dataSet): #对数据进行处理，获取我们要求的数据集格式
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1

    #返回字典类型{frozenset({'j', 'h', 'z', 'r', 'p'}): 1, frozenset({'y', 'v', 'x', 'w', 'u', 's', 't', 'z'}): 1...}
    return retDict

#三：根据createInitSet方法得到的数据集类型，创建FP树 和 FP条件树
#1.建树主函数
def createTree(dataSet,minSup=1):
    headerTable = {}    #存放头指针表
    for trans in dataSet:   #遍历数据,注意我们使用dataSet.items()可以遍历(key,val)对，直接遍历dataSet是对key的操作
        for item in trans:  #item是frozenset类型
            headerTable[item] = headerTable.get(item,0) + dataSet[trans]    #计数操作，其中dataSet[trans]返回字典对于values

    #重点：进行初次剪枝，去掉那些单个元素支持度太低的数据元素
    keys = list(headerTable.keys())
    for k in keys:
        if headerTable[k] < minSup:
            del(headerTable[k]) #达到剪枝效果

    #检查剪枝后是否还有数据存在
    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0:
        return None,None    #因为我们在正常情况下，返回的数据是FP树和头指针表

    #修改头指针表的格式，使得可以指向同类节点（实现链表操作）
    for k in headerTable:
        headerTable[k] = [headerTable[k],None]  #多出的None用来保存后面需要的节点信息

    #先产生根节点
    retTree = treeNode("Null Set",1,None)   #节点名称，出现次数，父节点

    #开始建树
    for tranSet,count in dataSet.items():
        localD = {} #用来保存本样本frozenset({'j', 'h', 'z', 'r', 'p'}): 1的keys是否是频繁项集
        for item in tranSet:
            if item in freqItemSet: #是在频繁项集中
                localD[item] = headerTable[item][0] #添加到localD保存次数
        if len(localD) > 0: #如果在本次样本中有数据在频繁项集中，则开始进行更新树---重点
            #对我们得到的临时localD频繁项集进行排序，将在更新树按照出现最高顺序进行更新（例如最大堆，但不是）
            orderItems = [v[0] for v in sorted(localD.items(),key=lambda p:p[1],reverse=True)]  #大到小排序
            updateTree(orderItems,retTree,headerTable,count)

    return retTree,headerTable  #返回我们需要的树和头指针表

#2.按照传入的一个样本frozenset({'j', 'h', 'z', 'r', 'p'})《注意：是排序好的，大到小》，对树进行更新
def updateTree(items,inTree,headerTable,count):
    """
    重点：我们使用递归方法建树
    :param items: 是传入的排序好的样本frozenset({'j', 'h', 'z', 'r', 'p'})
    :param inTree: 是我们要建立的树
    :param headerTable: 是我们要对头指针表进行修改节点指向，
    :param count: 是本样本在数据集中出现的次数
    """
    if items[0] in inTree.children: #已经存在该增加计数
        inTree.children[items[0]].inc(count)    #增加计数
    else:   #开始进行新增节点
        inTree.children[items[0]] = treeNode(items[0],count,inTree)  #节点按照特定的数据结构修改
        #由于我们有新增的节点，所以我们需要更新头指针表中的nodeLink链表信息，达到链表将同类型的节点链接
        if headerTable[items[0]][1] == None:    #原本不存在，则直接添加
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:   #找到同类节点的链路中的末尾，进行添加
            updateHeader(headerTable[items[0]][1],inTree.children[items[0]])    #更新头指针表

    #注意：由于我们的样本中有多个排序好的数据，所以，我们需要递归更新下面的数据
    if len(items) > 1:
        updateTree(items[1::],inTree.children[items[0]],headerTable,count)

#3.更新头指针表
def updateHeader(headerNode,newNode):
    while headerNode.nodeLink != None:
        headerNode = headerNode.nodeLink
    headerNode.nodeLink = newNode

#四：开始从上面获取的FP树中，获取各个数据的条件模式基
#1.从FP树种获取头指针表中的各个数据的条件模式基（即找前缀路径，设置计数为当前节点计数值）
def findPrefixPath(treeNode):   #书本上多了一个参数？？这里直接传我们指定的节点，查找前缀路径
    condPats = {}
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode,prefixPath) #获取前缀路径
        #保存前缀路径，和计数值
        if len(prefixPath) > 1: #保证除了本身节点之外，还存在其他前缀
            condPats[frozenset(prefixPath[1:])] = treeNode.count    #注意：使用frozenset类型作为key,并且保存时不含有本身节点
        treeNode = treeNode.nodeLink    #遍历下一个同类型节点

    return condPats #返回所有的前缀路径

#2.向上递归遍历树，找前缀节点信息
def ascendTree(treeNode,prefixPath):    #将结果保存在prefixPath中
    while treeNode.parent != None:  #除了根节点（无用）之外，都进行添加节点
        prefixPath.append(treeNode.name)
        treeNode = treeNode.parent

#五：开始查找频繁集（注意：上面只对单个数据进行了一次支持度裁剪，下面会对各个组合进行裁剪）
#根据条件基模型来构建条件FP树
def mineTree(headerTable,minSup,preFix,freqItemList):
    """
    :param headerTable: 是我们生成FP树时，生成的头指针表
    :param minSup: 最小支持度，用来对复合的数据进行筛选
    :param preFix: 首次为空集合，用来保存当前前缀
    :param freqItemList: 首次为空列表，用来保存所有的频繁项集
    """
    #对头指针表中的元素按照支持度（出现频率）从小到大排序
    bigL = [v[0] for v in sorted(headerTable.items(),key=lambda p:p[1][0])]
    #从满足最小支持度的头指针表的最小元素开始，遍历头指针表，挖掘频繁数据项
    for basePat in bigL:    #最好只思考一次循环数据
        #保存当前前缀路径
        newFreqSet = preFix.copy()
        #将当前频繁元素加入频繁集合中（这里就是将头指针表元素加入---已经是满足的）
        newFreqSet.add(basePat) #都是frozenset类型---------注意：
        #1.newFreqSet.add(basePat)这一步我们可以看案例I5推导，这里先加入I5，再获取条件FP树，
        #之后根据HeaderTable判断是否为None
        #由案例可知，返回非None,
        #2.对headerTable中I2 I1建树，newFreqSet中含有I5，再分别加上I1，I2
        #2.1先加上I1，即得到I1 I5
        #之后根据HeaderTable判断是否为None
        #由案例可知，返回非None,
        #2.1.1对headerTable中I2建树，newFreqSet中含有I1 I5，再加上I2 即可得到I2 I1 I5
        #2.2再在I5基础上，加上I2，即可得到I2 I5
        #之后根据HeaderTable判断是否为None
        #由案例可知，返回None,退出
        #得到I2 I5， I1 I5，    I2 I1 I5

        #将每个频繁元素添加到频繁项集列表中
        freqItemList.append(newFreqSet)
        #将每个频繁项，都调用findPrefixPath函数，找到前缀路径
        condPattBases = findPrefixPath(headerTable[basePat][1])
        #重点：根据当前元素项生成的前缀路径和最小支持度，生成条件FP树（内部会增加计数值）
        myCondTree,myHead = createTree(condPattBases,minSup)    #从这里可以看出，我们要保存原始数据和前缀路径发现函数返回相同数据类型
        #如果条件FP树中有元素项，则可以再次递归生成条件树
        if myHead != None:  #所以对于我们新的myHead必须在使用条件模型基时，满足最小支持度
            #递归挖掘该条件树，每次向上推一个节点（条件模型基都不包含本节点，所以一直在向上走）
            mineTree(myHead,minSup,newFreqSet,freqItemList)

dataSet = createInitSet(loadSimDat())
tree,headertable = createTree(dataSet,3)    #注意：因为我们建树的时候，支持度相同的节点不止一个，比如t:3,s:3，所以建树结果顺序可能不同
freqItemList = []
mineTree(headertable,3,set([]),freqItemList)
print(freqItemList)

十：再回头去看案例二，更好的理解八中挖掘频繁集

https://wenku.baidu.com/view/5a28e351bed126fff705cc1755270722182e594b.html

本文较为简略，后面需要再次理解。最近时间紧，任务重....,没有结合关联分析