一:图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
在图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
顶点:
线性表中我们把数据元素叫元素,树中数据元素叫结点,在图中数据元素,我们则称之为顶点
边:
线性表中,相邻的数据元素之间具有线性关系,树中,相邻两层的结点中具有层次关系,图中任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示
二:有向图和无向图
图按照边的有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。
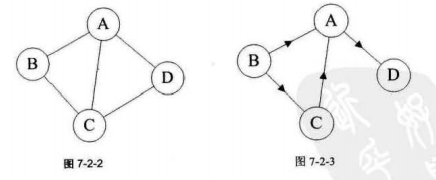
无向边:
若顶点v1到v2之间的边没有方向,就是无向边,使用(v1,v2)表示
有向边:
若顶点v1到顶点v2的边有方向,则称这条边为有向边,又称为弧,使用<v1,v2>表示,其中v1为弧尾,v2为弧头,v1--->v2,有向边的两个顶点不能交换
三:简单图
图中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
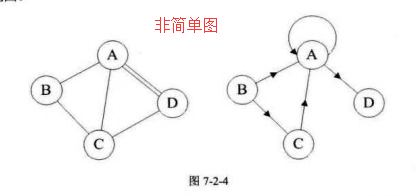
我们讨论的都是简单图
四:无向完全图和有向完全图
无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。有n个顶点的完全无向图有n(n-1)/2 条边
有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称改图为有向完全图。含有n*(n-1)条边
五:稀疏图和稠密图
按照边或弧的多少来分稀疏图和稠密图。大于n*logn为稠密图,反之为稀疏图
六:网(网络)
有些图的边或弧具有与他相关的数字,这种与图的边或弧相关的数叫做权(Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网(Network)
七:子图
假设有两个图G= (V,{E})和G'= (V',{E'}),如果V'是V的子集,且E'是E的子集,则称G'为G的子图。如下图带底纹的图均为左侧无向图与有向图的子图。
八:图的顶点和边之间的关系
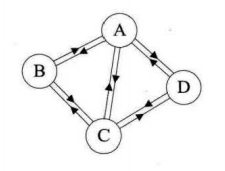
(一)度
无向图的度
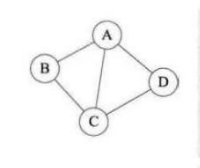
对于无向图G= (V,{E}), 如果边(v,v')属于E, 则称顶点v和v‘互为邻接点,即v和v'相邻接、边(v,v')依附于顶点v和v',或者说(v,v')与顶点v和v'相关联。
顶点v的度是和v相关联的边的数目,记为TD(v)。
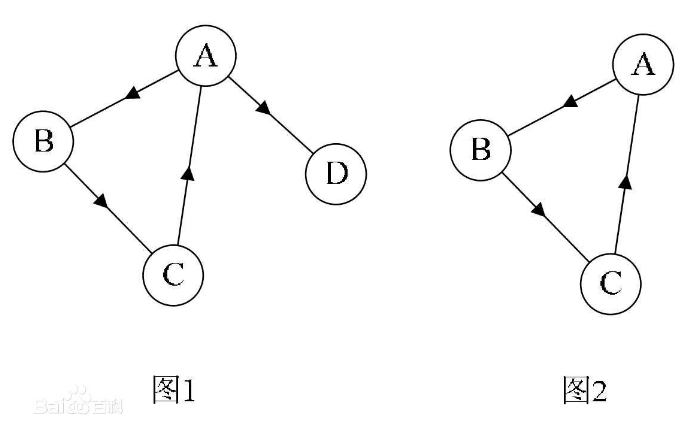
如上图左侧上方的无向图,顶点A与B 互为邻接点,边(A,B) 依附于顶点A 与B 上,顶点A 的度为3。
而此图的边数是5,各个顶点度的和=3+2+3+2=10,
推敲后发现,边数其实就是各顶点度数和的一半,多出的一半是因为重复两次计数。
有向图的度
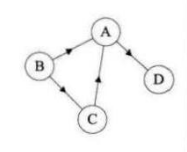
对于有向图G= (V,{E}),如果弧<v,v'>属于E,则称顶点v邻接到顶点v',顶点v'邻接自顶点v的弧<v,v'>和顶点v, v'相关联。
以顶点v为头的弧的数自称为v的入度 ,记为ID (v); 以v为尾的弧的数目称为v的出度,记为OD (v); 顶点v的度为TD(v) =ID(v) +OD (v)。
上图 左侧下方的有向图,顶点A的入度是2 (从B到A的弧,从C到A的弧),出度是1 (从A到D的弧),所以顶点A 的度为2+1=3。此有向图的弧有4 条,而各顶点的出度和=1+2+1+0=4,各顶点的入度和=2+0+1+1=4。
(二)路径
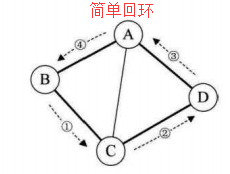
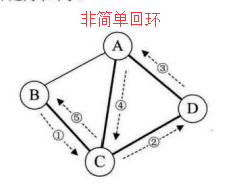
路径的长度是路径上的边或弧的数目
第一个顶点到最后一个顶点相同的路径称为回路或环
序列中顶点不重复出现的路径称为简单路径
除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路或简单环
九:连通图
连通图(无向图)
在无向图G中,如果从顶点v到顶点v'有路径,则称v和v'是连通的。
如果对于图中任意两个顶点vi、vj ∈E, vi,和vj都是连通的,则称G是连通图。
下图的图1,它的顶点A到顶点B、 C、 D都是连通的,但显然顶点A与顶点E或F就无路径,因此不能算是连通图。而图2,顶点A、 B、 C、D相互都是连通的,所以它本身是连通图。
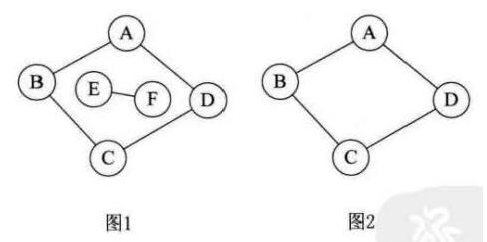
连通分量
无向图中的极大连通子图称为连通分量。
连通分量需要满足:
1.要是子图;
2.子图要是连通的;
3.连通子图含有极大顶点数;
4.具有极大顶点数的连通子图包含依附于这些顶点的所有边。
上图中,图1是一个无向非连通图。 但是有两个连通分量,即图2和图3。
而图4,尽管是图1的子图,但是它却不满足连通子图的极大顶点数(图2满足)。 因此它不是图1的无向图的连通分量。
强连通图(有向图)
在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。
有向图中的极大强连通子图称做有向图的强连通分量。强
连通图具有如下定理:一个有向图G是强连通的,当且仅当G中有一个回路,它至少包含每个节点一次。
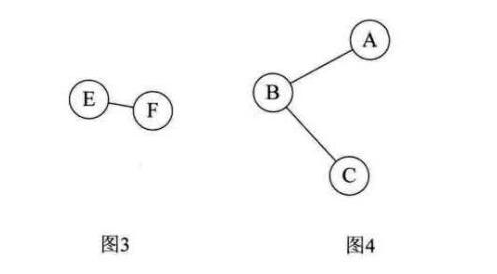
图一不是强连通图,图二是强连通图。
图二是图一的强连通分量
十:连通图的生成树
所谓的一个连通图的生成树是一个极小的连通子图, 它含有图中全部的n 个顶点,但只有足以构成一棵树的n-1条边。
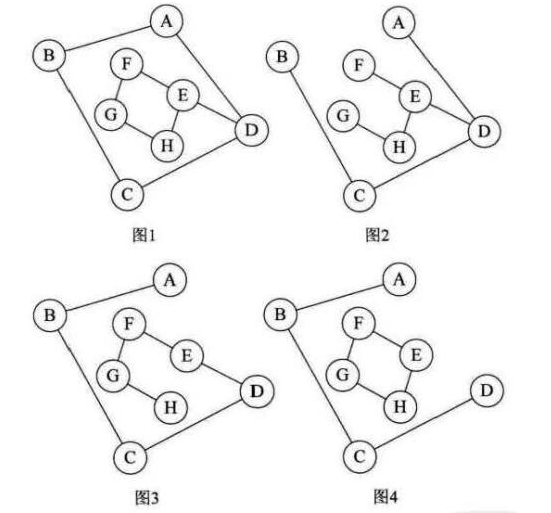
比如下图的图1是一连通图,但显然它不是生成树,当去掉两条构成环的边后,比如图2 或图3,就满足n个顶点n-1条边且连通的定义了, 它们都是一棵生成树。
从这里也可知道,如果一个图有n 个顶点和小于n-1条边,则是非连通图,如果多于n-1 边条,必定构成一个环, 因为这条边使得它依附的那两个顶点之间有了第二条路径。比如图2 和图3,随便加哪两顶点的边都将构成环。
不过有n-1条边并不一定是生成树,比如图4。
十一:有向图的生成森林
如果一个有向图恰有一个顶点的入度为0,其余顶点的入度均为1,则是一棵有向树。
对有向树的理解比较容易,所谓入度为0其实就相当于树中的根结点, 其余顶点入度为1就是说树的非根结点的双亲只有一个。
一个有向图的生成森林由若干棵有向树组成, 含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。
如下图的图1 是一棵有向图。去掉一些弧后,它可以分解为两棵有向树,如图2和图3,这两棵就是图1有向图的生成森林。

十二:术语总结



