2019 ICPC Universidad Nacional de Colombia Programming Contest 题解

目录

• 2019 ICPC Universidad Nacional de Colombia Programming Contest 题解
  • A. Amazon
  • B. Boring Non-Palindrome
  • C. Common Subsequence
  • D. Do Not Try This Problem
  • E. Extreme Image
  • F. Fraction Formula
  • G. Graduation
  • H. Hardest Challenge
  • I. Integer Prefix
  • J. Jail Destruction
  • K. Kernel Of Love
  • L. Liquid X

2019 ICPC Universidad Nacional de Colombia Programming Contest 题解

最近比较忙，题解写的有点水

A. Amazon

题意：给定 (n) 条直线，两条相互垂直的直线交点处要修建一个十字路口，询问需要修建几个十字路口。

分析：这题题意相当坑，并不是求相互垂直的直线的不同交点数量，而是不同的“十字路口数量”，这有什么区别呢？参考下图：

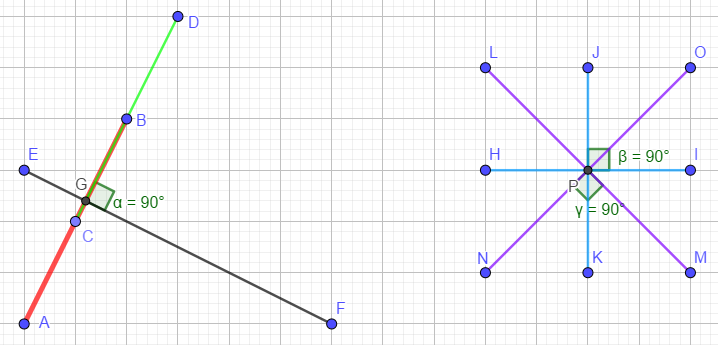
左边虽然有两对相互垂直的直线，但只要建一个“十字路口”，但右边需要建两个。

看明白题意之后这题就不难了，跟 CCPC2019 秦皇岛站 A. Angle Beats 的做法是一样的，把所有直线用最简形式的向量存储，删除共线后计数即可。

#include <bits/stdc++.h>
#define mp make_pair
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }

int __gcd(int a, int b) {
	return b == 0 ? a : __gcd(b, a % b);
}

int main() {
	io(); int t;
	cin >> t;
	while (t--) {
		int n; cin >> n;
		vector<pair<pair<int, int>, int> > p;
		map<pair<int, int>, int> MP;
		for (int i = 1; i <= n; ++i) {
			int xa, ya, xb, yb;
			cin >> xa >> ya >> xb >> yb;
			int x = xb - xa, y = yb - ya;
			int g = __gcd(x, y);
			x /= g, y /= g;
			if (y < 0) x = -x, y = -y;
			else if (y == 0) x = abs(x);
			p.emplace_back(mp(mp(x, y), xa * y - ya * x));
		}
		sort(p.begin(), p.end());
		p.erase(unique(p.begin(), p.end()), p.end());

		for (auto it : p) MP[it.first]++;
		ll ans = 0;
		for (auto it : p) {
			int x = it.first.second, y = -it.first.first;
			if (y < 0) x = -x, y = -y;
			else if (y == 0) x = abs(x);
			ans += MP[mp(x, y)];
		}
		cout << ans / 2ll << '
';
	}
}

B. Boring Non-Palindrome

题意：略。

分析：水题。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }

int main() {
	io(); string x, y;
	cin >> x;
	y = x; reverse(y.begin(), y.end());
	for (int i = 0; i <= x.length(); ++i) {
		string p = y.substr(y.size() - i, i);
		string tmp = x + p;
		string tp = tmp;
		reverse(tp.begin(), tp.end());
		if (tp == tmp) {
			cout << tmp;
			return 0;
		}
	}
}

C. Common Subsequence

题意：给定两个由 (A,C,G,T) 构成的长度为 (n) 的字符串，求出他们的最长公共子序列，然后判断这个子序列的长度和 (0.99n) 的大小关系。

分析：(dp) ，队友秒了。

#include<bits/stdc++.h>
#define ll long long
#define maxn 100100
#define mod 998244353
using namespace std;
int dp[1010][1010];
char s1[maxn], s2[maxn];
int main() {
	scanf("%s%s", s1, s2);
	int n = strlen(s1);
	int m = n / 100 + 1;
	int ans = 0;
	for (int i = 0; i <= m; i++) {
		for (int j = 0; j <= m; j++) {
			while (i + dp[i][j] < n && j + dp[i][j] < n && s1[i + dp[i][j]] == s2[j + dp[i][j]]) dp[i][j]++;
			dp[i + 1][j] = max(dp[i + 1][j], dp[i][j]);
			dp[i][j + 1] = max(dp[i][j + 1], dp[i][j]);
			ans = max(ans, dp[i][j]);
		}
	}
	if (ans * 100 >= n * 99) printf("Long lost brothers D:
");
	else printf("Not brothers :(
");
	return 0;
}

D. Do Not Try This Problem

题意：给定一个字符串 (s) ，(q) 次修改，每次将 (i+ak) 这些位置的字母修改，询问修改完后的字符串。

分析：数据水，暴力剪枝假算法过了。

#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define mp make_pair
#define SIZE 100010
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
vector<pair<int, char> > in[SIZE];
vector<pair<int, char> > out[SIZE];

int main() {
	io(); string s;
	cin >> s;
	s = " " + s;
	int q; cin >> q;
	vector<int> lazy(s.length(), 0);
	for (int i = 1; i <= q; ++i) {
		int p, a, k; char c;
		cin >> p >> a >> k >> c;
		if (a == 1) {
			in[p].emplace_back(mp(i, c));
			out[p + k + 1].emplace_back(mp(i, c));
		}
		else {
			for (int j = 0; j <= k; ++j) {
				s[p + a * j] = c;
				lazy[p + a * j] = i;
			}
		}
	}
	set<pair<int, char> > st;
	for (int i = 1; i < s.length(); ++i) {
		for (auto it : in[i])
			if (!st.count(it))
				st.insert(it);
		for (auto it : out[i])
			if (st.count(it))
				st.erase(it);
		if (st.size()) {
			if (st.rbegin()->first > lazy[i]) cout << st.rbegin()->second;
			else cout << s[i];
		}
		else cout << s[i];
	}
}

E. Extreme Image

题意：求一个扇形（剪掉一个小扇形）区域内最多能覆盖多少点。

分析：(POJ2482) 翻版，从水平扫描线变成旋转扫描线，不过还是一个标准的扫描线+线段树裸题。

#include<bits/stdc++.h>
#define ll long long
#define maxn 100100
#define mod 998244353
#define eps 1e-8
using namespace std;
struct cv {
	int x, y;
}a[maxn * 2];
bool cmp(cv p, cv q) {
	return p.y < q.y;
}
int tr[maxn * 4], lz[maxn * 4];
void up(int x) {
	tr[x] = max(tr[x * 2], tr[x * 2 + 1]);
}
void pe(int x) {
	if (lz[x]) {
		tr[x * 2] += lz[x];
		tr[x * 2 + 1] += lz[x];
		lz[x * 2] += lz[x];
		lz[x * 2 + 1] += lz[x];
		lz[x] = 0;
	}
}
void cg(int x, int l, int r, int s, int e, int y) {
	if (l >= s && r <= e) {
		tr[x] += y;
		lz[x] += y;
		return;
	}
	pe(x);
	int mid = (l + r) / 2;
	if (mid >= s) cg(x * 2, l, mid, s, e, y);
	if (mid < e) cg(x * 2 + 1, mid + 1, r, s, e, y);
	up(x);
}
int main() {
	int n, d, w;
	double wi;
	scanf("%d%d%lf", &n, &d, &wi);
	w = (int)(wi * 100 + eps);
	for (int i = 0; i < n; i++) {
		scanf("%d%lf", &a[i].x, &wi);
		a[i].y = (int)(wi * 100 + eps);
	}
	sort(a, a + n, cmp);
	for (int i = 0; i < n; i++) {
		a[i + n] = a[i];
		a[i + n].y += 36000;
	}
	n *= 2;
	int l = 0, r = 0, ans = 0;
	memset(tr, 0, sizeof(tr));
	memset(lz, 0, sizeof(lz));
	while (r < n) {
		int cnt = 0;
		for (int i = r; i < n; i++) {
			if (a[i].y == a[r].y) {
				cg(1, 0, 100000, max(0, a[i].x - d), a[i].x, 1);
				cnt++;
			}
			else break;
		}
		while (l < r) {
			if (a[r].y - a[l].y > w) {
				cg(1, 0, 100000, max(0, a[l].x - d), a[l].x, -1);
				l++;
			}
			else break;
		}
		r += cnt;
		ans = max(ans, tr[1]);
	}
	printf("%d
", ans);
	return 0;
}

F. Fraction Formula

题意：给出一个式子，求结果。

分析：分数类大模拟，注意必定爆 (int) ，如果运算顺序不好还会爆 (long long) 。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
#define int LL

const int maxn = 2e5 + 5;
char s[maxn];
struct Fac {
    int x;
    int y;
    Fac() {}
    Fac(int x, int y) : x(x), y(y) {}

    void change() {
        x *= -1;
    }

    void trans() {
        if (!y) return;
        if (!x) {
            y = 1;
            return;
        }
        int gcd = __gcd(x, y);
        x /= gcd;
        y /= gcd;
        if (y < 0) {
            y *= -1;
            x *= -1;
        }
    }

    Fac friend operator+(const Fac& a, const Fac& b) {
        int lcm = a.y / __gcd(a.y, b.y) * b.y;
        int x1 = a.x * (lcm / a.y), x2 = b.x * (lcm / b.y);
        Fac res(x1 + x2, lcm);
        res.trans();
        return res;
    }

    void print() {
        cout << x << "/" << y << '
';
    }
};

vector<Fac> res;
vector<int> fres;
signed main() {
    while (~scanf("%s", s + 1)) {
        res.clear();
        int g = 1;
        fres.clear();
        fres.push_back(1);

        int len = strlen(s + 1);
        int f = g;
        for (int i = 1; i <= len; i++) {
            if (s[i] == '-') f *= -1;
            else if (s[i] == '+') f *= 1;
            else if (s[i] >= '0' && s[i] <= '9') {
                int x = 0, y = 0, ff = 1;
                while (s[i] != '/')
                    x = x * 10 + s[i] - '0',
                    i++;
                i++;
                if (s[i] == '-')
                    ff *= -1, i++;
                while (s[i] >= '0' && s[i] <= '9')
                    y = y * 10 + s[i] - '0',
                    i++;
                i--;

                Fac a = Fac(x, y);
                a.trans();
                if (f * ff == -1) a.change();
                f = g;

                if (res.empty()) res.push_back(a);
                else res.back() = res.back() + a;
            } else if (s[i] == '(') {
                fres.push_back(f);
                g = fres.back();
                f = g;
            } else if (s[i] == ')') {
                fres.pop_back();
                g = fres.back();
                f = g;
            }
        }
        res.back().trans();
        res.back().print();
    }
    return 0;
}

G. Graduation

我也不知道是啥，队友秒了。

#include<bits/stdc++.h>
#define ll long long
#define maxn 10010
#define mod 998244353
using namespace std;
vector<int>b[maxn];
int ans[maxn];
void sol(int x, int d) {
	ans[d]++;
	for (int i = 0; i < b[x].size(); i++) {
		sol(b[x][i], d + 1);
	}
}
int main() {
	int n, k;
	scanf("%d%d", &n, &k);
	for (int i = 1; i <= n; i++) {
		int x;
		scanf("%d", &x);
		b[x].push_back(i);
	}
	sol(0, 0);
	int r = maxn - 1;
	while (!ans[r]) r--;
	int sum = 0, num = 0;
	for (int i = r; i > 0; i--) {
		sum += ans[i];
		num++;
		while (num * k < sum) num++;
	}
	printf("%d
", num);
	return 0;
}

H. Hardest Challenge

题意：略。

分析：折半搜索。

#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 5000100
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
const ll mod = 1e15 + 37;
vector<string> s(3);
ll a[SIZE], b[SIZE], p[30];
int pa, pb, n, m;

void dfs(int pos, ll sum, ll a[], int& cnt, int m) {
	if (pos == m) {
		a[cnt++] = sum;
		return;
	}
	for (int i = 0; i < 3; ++i) {
		ll tmp = (sum + 1ll * s[i][pos] * p[n - 1 - pos] % mod) % mod;
		dfs(pos + 1, tmp, a, cnt, m);
	}
}

ll solve() {
	for (int i = 0; i < 3; ++i) cin >> s[i];
	n = s[0].length();
	pa = pb = 0;
	m = n >> 1;
	dfs(0, 0, a, pa, m);
	dfs(m, 0, b, pb, n);
	sort(a, a + pa);
	sort(b, b + pb);
	a[pa] = a[0] + mod;
	b[pb] = b[0] + mod;
	int pos = pa;
	ll ans = mod;
	for (int i = 0; i < pb; ++i) {
		while (pos > 0 && b[i] + a[pos - 1] >= mod) --pos;
		ans = min(ans, a[pos] + b[i] - mod);
	}
	return ans;
}

int main() {
	io(); p[0] = 1;
	for (int i = 1; i < 30; ++i) p[i] = p[i - 1] * 127ll % mod;
	int x; cin >> x >> x;
	ll A = solve();
	ll B = solve();
	if (A < B) cout << "Owls";
	else if (A > B) cout << "Goats";
	else cout << "Tie";
}

I. Integer Prefix

题意：找最长的前缀数字。

分析：签到。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }

int main() {
	io(); string s;
	cin >> s;
	bool f = false;
	for (auto i : s) {
		if (i >= '0' && i <= '9') {
			f = true;
			cout << i;
		}
		else break;
	}
	if (!f) cout << "-1";
}

J. Jail Destruction

队友说是简单的线段树。

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e5 + 5;
typedef long long LL;
int a[maxn];
namespace Segement {
	const LL inf = 0X3f3f3f3f3f3f3f3f;
	LL tree[maxn << 2], vis[maxn << 2], h[maxn << 2];
	LL lazy[maxn << 2];
	void build(int root, int left, int right)
	{
		if (left == right) {
			vis[root] = 1;
			h[root] = tree[root] = a[left];
			return;
		}
		int mid = (left + right) >> 1;
		build(root << 1, left, mid);
		build(root << 1 | 1, mid + 1, right);
		h[root] = min(h[root << 1], h[root << 1 | 1]);
		vis[root] = vis[root << 1] + vis[root << 1 | 1];
		tree[root] = tree[root << 1] + tree[root << 1 | 1];
	}
	void pushdown(int root)
	{
		if (!lazy[root])
			return;
		h[root << 1] -= lazy[root];
		h[root << 1 | 1] -= lazy[root];
		tree[root << 1] -= vis[root << 1] * lazy[root];
		tree[root << 1 | 1] -= vis[root << 1 | 1] * lazy[root];
		lazy[root << 1] += lazy[root];
		lazy[root << 1 | 1] += lazy[root];
		lazy[root] = 0;
	}
	void update(int root, int left, int right, int stdl, int stdr, LL val)
	{
		if (left >= stdl && right <= stdr && val <= h[root]) {
			h[root] -= val;
			tree[root] -= vis[root] * val;
			lazy[root] += val;
			return;
		}
		if (left == right && h[root] < val) {
			tree[root] = vis[root] = 0;
			h[root] = inf;
			return;
		}
		pushdown(root);

		int mid = (left + right) >> 1;
		if (stdl <= mid)
			update(root << 1, left, mid, stdl, stdr, val);
		if (stdr > mid)
			update(root << 1 | 1, mid + 1, right, stdl, stdr, val);
		h[root] = min(h[root << 1], h[root << 1 | 1]);
		vis[root] = vis[root << 1] + vis[root << 1 | 1];
		tree[root] = tree[root << 1] + tree[root << 1 | 1];
	}
	LL query(int root, int left, int right, int stdl, int stdr)
	{
		if (left >= stdl && right <= stdr) {
			return tree[root];
		}
		pushdown(root);

		LL res = 0;
		int mid = (left + right) >> 1;
		if (stdl <= mid)
			res += query(root << 1, left, mid, stdl, stdr);
		if (stdr > mid)
			res += query(root << 1 | 1, mid + 1, right, stdl, stdr);
		return res;
	}
}

int main()
{
	int n, q;
	scanf("%d%d", &n, &q);
	for (int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	Segement::build(1, 1, n);

	int p, a, b, w;
	while (q--) {
		scanf("%d", &p);
		if (p == 1) {
			scanf("%d%d", &a, &b);
			LL ans;
			if (a <= b)
				ans = Segement::query(1, 1, n, a, b);
			else
				ans = Segement::query(1, 1, n, a, n) + Segement::query(1, 1, n, 1, b);
			printf("%lld
", ans);
		}
		else {
			scanf("%d%d%d", &a, &b, &w);
			if (a <= b)
				Segement::update(1, 1, n, a, b, w);
			else
				Segement::update(1, 1, n, a, n, w),
				Segement::update(1, 1, n, 1, b, w);
		}
	}

	return 0;
}

K. Kernel Of Love

队友说是签到。

#include <bits/stdc++.h>
using namespace std;
 
int main()
{
    int t;
    scanf("%d", &t);
 
    while (t--) {
        int n;
        scanf("%d", &n);
 
        int ans = n / 3;
        if (ans)
            ans = (ans - 1) * 2 + 1;
        if (n / 3 && n % 3)
            ans++;
 
        if (n >= 3)
            ans++;
        printf("%d
", ans);
    }
 
    return 0;
}

L. Liquid X

题意：交互题，给定一堆试管，每次能够用这些试管加入试剂，加多了会变红，少了会变绿，正好会变黄，询问应该加多少试剂，或者判断不能求出应该加入多少试剂。

分析：用背包把所有可以表示的求出来，然后二分。

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e6 + 5;
bool dp[maxn];
int pre[maxn], p[maxn];

int n, a[105], vis[105];
int cnt[maxn];

void check(int mid)
{
    int now = cnt[mid];
    memset(vis, 0, sizeof(vis));
    while (now) {
        vis[p[now - pre[now]]]++;
        now = pre[now];
    }
    printf("1
");
    for (int i = 1; i <= n; i++)
        printf("%d ", vis[i]);
    printf("
");
    fflush(stdout);
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    int limit = 1e6;
    dp[0] = true;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= limit - a[i]; j++)
            if (dp[j])
                dp[j + a[i]] = true,
                       pre[j + a[i]] = j;
    }
    int k = 0;
    for (int i = 1; i <= limit; i++)
        if (dp[i])
            cnt[++k] = i;

    for (int i = 1; i <= n; i++)
        p[a[i]] = i;
    char s[20];
    int left = 1, right = k, mid, ans = -1;
    while (left <= right) {
        mid = (left + right) >> 1;
        check(mid);
        scanf("%s", s + 1);
        if (s[1] == 'y') {
            ans = cnt[mid];
            break;
        } else if (s[1] == 'g')
            left = mid + 1;
        else
            right = mid - 1;
    }

    if (ans == -1) {
        if (cnt[mid] == 2 && s[1] == 'r')
            ans = 1;
        if (cnt[mid] == limit - 1 && s[1] == 'g')
            ans = limit;
        if (abs(cnt[right] - cnt[left]) == 2)
            ans = min(cnt[left], cnt[right]) + 1;
    }

    printf("2
%d
", ans);
    fflush(stdout);

    return 0;
}