在前一篇文章中提到了光子映射算法具有高效,扩展性好,能轻易捕捉到各种光照效果(比如Monte Carlo ray tracing不易捕捉到的SDS路径),但是它也存在很多问题,比如它本身是一个有偏的算法,boundary bias和topological bias通常能造成肉眼可见的artifact,这主要表现为灰暗的墙角,错误的颜色辉映以及漏光等现象。
针对这一问题,Havran等人在05年提出了以搜集光子射线代替搜集光子本身来解决boundary bias,该方法在采样点切平面上创建一个圆形区域,经过此区域的photon ray将被搜集到,但是为了高效地进行photon ray gathering,需要建立复杂的数据结构比如ray map。紧接着,在07年由Herzog等人提出了photon ray splatting以代替photon ray gathering,该方法将整个光子映射算法流程倒了过来,即先进行eye tracing,再进行photon tracing。在eye tracing过程中,我们像raytrace那样对视平面每个像素点发射射线,在击中漫反射表面后将交点信息存放起来(若击中镜面则需存储后继射线的交点信息),一般用kd-tree作为数据结构;第二步photon tracing中,从光源每发射光子后,每击中一个物体表面,就查询之前建立好的eye sample kd-tree以确定对哪些屏幕像素点产生颜色值贡献。在Herzog的算法中光源每次发射的是一个带宽度的光子,如下图:
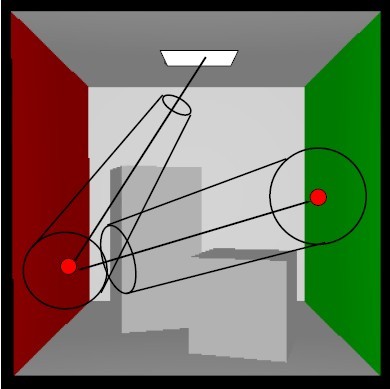
因而当光子击中场景时,会对一定范围内的eye sample点产生颜色值贡献,下图显示了标准光子映射(左),photon ray gathering(中),photon ray splatting(右)算法中光子搜集方式的不同:
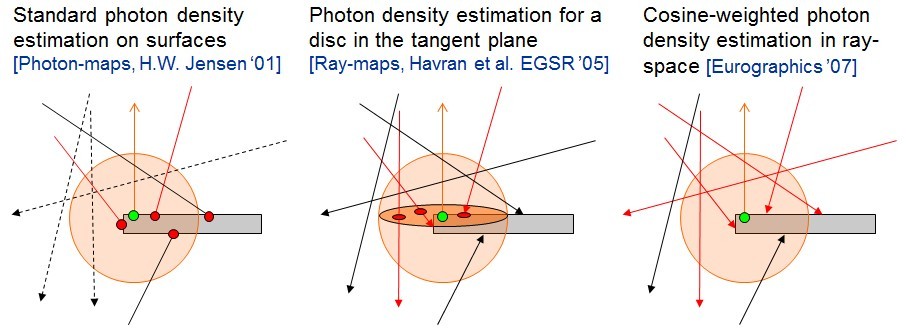
可见,从eye sample(绿点)附近经过的photon ray都被搜集到了,而击中背面的photon ray则可以利用一个可见性判别剔除掉,这样就有效地解决了boundary bias和topological bias的问题。但是它仍然不能解决proximity bias,这种由于密度估计范围r的不趋于零而存在的一种偏差,要解决这一问题,就必须想办法将光子数量扩大到无穷大,以便将r减小,但是如何存储同时怎么多光子呢?实际上,借用photon ray splatting中倒转光子映射算法流程的思想,可以破除光子映射中内存的限制,原因很简单,因为屏幕像素有限,所以要存下eye sample到内存是很轻松的事情,那么光子图根本就不需要存储,这样要多少光子就可以发射多少光子。
08年,由Hachisuka等人提出了渐进式光子映射(Progressive Photon Mapping),通过第一步将eye sample组织成一个kd-tree结构,而后一轮轮地发射光子,每一轮将r减小一次,每一轮渲染一张图片。随着轮数的增多,光子数量越来越多,r的值越来越小,最终结果也越来越好,这样PPM算法也使得光子映射能生成任意精准度的图片,只要时间允许。由于倒转了PM算法的步骤顺序,PPM算法的光子搜集方法又从KNN变回到了直方图估计,这是因为每一轮中估计半径r一定是一个定值,虽然KNN估计在光子密度稀少处能更好地降低噪声,但是由于PPM算法本身已经没有了光子数量的限制,所以这点劣势很容易以大量的光子数量扳回。有了PPM,我们甚至可以不需要final gathering,因为final gathering本身也极其耗时,且不能消除偏差,还没有PPM算法自然简洁。但是该算法也远非没有问题。由于预先存储了eye sample,所以PPM无法很好地完成分布式光线跟踪里可以完成的任务,如果是像反走样这样简单的活还可以依靠在eye sample kd-tree中存下每个像素点的所有超采样点来完成的话,那么要模拟反射模糊,景深,运动模糊就更麻烦了。
09年,还是Hachisuka,在PPM算法稍作改进,提出了SPPM(Stochastic Progressive Photon Mapping),该算法与PPM不同之处在于,在每一轮光子发射完毕后重新进行一次eye tracing,并且每次eye tracing都带上一个随机的扰动,让每次构建的eye sample kd-tree中的数据都不一样,下图展示了这两个算法的区别:

这样做使得SPPM效率上略低于PPM,但是换来的是更加健壮和灵活,实际上SPPM在处理gloss反射的时候效果远好于PPM。看到这里,我们可能会想,既然可以一轮轮地发射光子,那不倒转整个PM算法流程也可以实现,即每次发射一定数量的光子,存起来,用完了再删掉,再发射另外一拨光子。这确实是可行的,11年Claude Knaus等人就证明了这种方式和PPM算法具有同样的鲁棒性,由于和标准PM算法的极其相似,所以之前在标准PM算法中可用的扩展,这里也全部可用,这样这种方法也很容易处理烟雾等介质的渲染。
至此,可以看出,光子映射算法中的两个pass,代表了正向跟踪和逆向跟踪两种思想,就像之前的提到过的Light tracing和raytracing一样,两个方向相互对称,而它们每个都具有另一个所没有的优点,bidirectional pathtracing连接了正向与逆向两个路径,达到了比pathtracing高很多的效率,photon mapping同样利用了正向与逆向两个方向的信息,不仅如此,它还重用了信息(光子图),所以一般情况下能比bidirectional pathtracing收敛更快。
从古老的正向跟踪算法Monte Carlo Light Tracing中,可以看到正向跟踪普遍存在的问题,当场景空间很大,但是能被视点看到的部分却很小的时候,会有大量的采样点对最终图像额颜色值贡献很小甚至毫无贡献。PM算法中同样存在这一问题,当场景中光子分布很糟糕的时候(只有少部分光子能到达视点的可见范围)该算法的收敛速度会变得非常之慢。受到Metropolis light transport的启发,Fan Shaohua等人于05年将Metropolis准则引入了PM算法中的photon tracing中,使主要靠间接光照明的场景能达到更快的收敛速度;11年,Chen jiating等人在SPPM基础上加入Metropolis准则,同样提高了SPPM在这类场景的收敛速率。
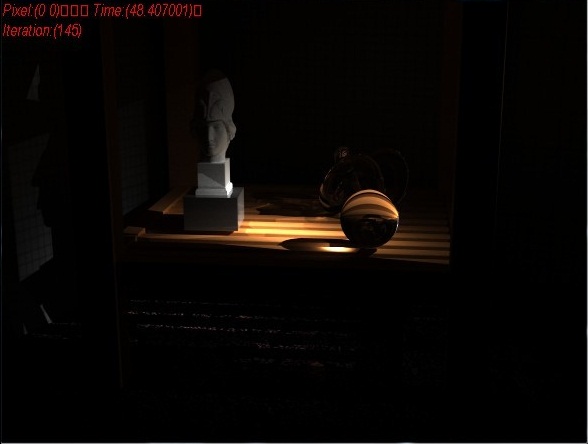
最后贴上是几张由PPM渲染的图片,由于没有了光子数量的限制,最终结果会比普通PM得到的结果更好: