【CSP-S 2019模拟】题解

T1：

一道很简单的线段树优化建图
点数边数大概在$O(nlogn)$

然后$Dinic$写太丑被卡常了

#include<bits/stdc++.h>
using namespace std;
const int RLEN=1<<20|1;
inline char gc(){
    static char ibuf[RLEN],*ib,*ob;
    (ob==ib)&&(ob=(ib=ibuf)+fread(ibuf,1,RLEN,stdin));
    return (ob==ib)?EOF:*ib++;
}
#define gc getchar
inline int read(){
    char ch=gc();
    int res=0,f=1;
    while(!isdigit(ch))f^=ch=='-',ch=gc();
    while(isdigit(ch))res=(res+(res<<2)<<1)+(ch^48),ch=gc();
    return f?res:-res;
}
#define ll long long
#define re register
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cs const
#define bg begin
template<class tp>inline void chemx(tp &a,tp b){a<b?a=b:0;}
template<class tp>inline void chemn(tp &a,tp b){a>b?a=b:0;}
cs int N=1000005;
cs int inf=1e9;
int n,m,tot,str,des;
struct edge{
	int v,cap,r;
	edge(int a=0,int b=0,int c=0):v(a),cap(b),r(c){}
};
vector<edge> e[N];
inline void addedge(int u,int v,int w){
	e[u].pb(edge(v,w,e[v].size()));
	e[v].pb(edge(u,0,e[u].size()-1));
}
#define It vector<edge>::iterator
namespace Flow{
	int lev[N];It tp[N];
	queue<int> q;
	inline bool bfs(){
		memset(lev,-1,sizeof(int)*(tot+1));
		lev[str]=0,q.push(str);
		while(!q.empty()){
			int u=q.front();q.pop();
			for(edge &x:e[u]){
				if(lev[x.v]==-1&&x.cap>0){
					lev[x.v]=lev[u]+1,q.push(x.v);
				}
			}
		}
		return lev[des]!=-1;
	}
	int dfs(int u,int flow){
		if(u==des)return flow;
		int res=0;
		for(It &it=tp[u];it!=e[u].end();it++){
			if(lev[it->v]==lev[u]+1&&it->cap>0){
				int now=dfs(it->v,min(it->cap,flow-res));
				res+=now,it->cap-=now,e[it->v][it->r].cap+=now;
				if(res==flow)break;
			}
		}
		return res;
	}
	inline int dinic(){
		int res=0;
		while(bfs()){
			for(int i=1;i<=tot;i++)tp[i]=e[i].bg();
			res+=dfs(str,1e9);
		}
		return res;
	}
}
namespace Seg{
	int node[N<<2],cov[N];
	#define lc (u<<1)
	#define rc ((u<<1)|1)
	#define mid ((l+r)>>1)
	inline void pushup(int u){
		node[u]=++tot;
		if(!cov[lc])addedge(node[u],node[lc],inf);
		if(!cov[rc])addedge(node[u],node[rc],inf);
	}
	void build(int u,int l,int r){
		if(l==r){node[u]=n+l;return;}
		build(lc,l,mid),build(rc,mid+1,r);
		pushup(u);
	}
	void update(int u,int l,int r,int st,int des,int k){
		if(st<=l&&r<=des){cov[u]+=k;return;}
		if(st<=mid)update(lc,l,mid,st,des,k);
		if(mid<des)update(rc,mid+1,r,st,des,k);
		pushup(u);
	}
}
struct opt{
	int l,r,op;
	opt(int a=0,int b=0,int c=0):l(a),r(b),op(c){}
};
vector<opt> p[N];
int main(){
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int x1=read(),y1=read(),x2=read(),y2=read();
		p[x1].pb(opt(y1,y2,1)),p[x2+1].pb(opt(y1,y2,-1));
	}
	tot=2*n+2,str=2*n+1,des=str+1;
	for(int i=1;i<=n;i++)addedge(str,i,1),addedge(i+n,des,1);
	Seg::build(1,1,n);
	for(int i=1;i<=n;i++){
		opt x;
		for(int j=0;j<p[i].size();j++){
			x=p[i][j];
			Seg::update(1,1,n,x.l,x.r,x.op);
		}
		if(!Seg::cov[1])addedge(i,Seg::node[1],1e9);
	}
	cout<<Flow::dinic();
}

T2：

开始 $rush2$个小时暴力失败导致没写完$T3$
当询问$Alice$的时候可以发现答案就是$n$
因为考虑如果跳过一个高度为$i$的
中间经过的楼房数量就是$2^i$
考虑枚举中间有几个房子等比数列算一下就可以得到了

考虑$Bob$时
考虑枚举高度$i$
即加入一个新的高度的绳子覆盖原来的
考虑枚举当前的长度$j$
那么可能在$n-j$个位置出现
概率是$(n-j)(1-frac{1}{2^i})^{j-1}*frac{1}{2^{2i}}$

考虑减去覆盖的上一个高度的期望（再之前的已经被减去了）
$i-1$的就是中间$j-1$个楼房中高度为$i-1$的个数的
个数就是$1+(j-1)*frac{1}{2^i-1}$

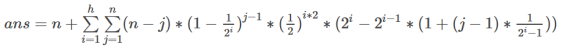
然后就完了

#include<bits/stdc++.h>
using namespace std;
const int RLEN=1<<20|1;
inline char gc(){
    static char ibuf[RLEN],*ib,*ob;
    (ob==ib)&&(ob=(ib=ibuf)+fread(ibuf,1,RLEN,stdin));
    return (ob==ib)?EOF:*ib++;
}
#define gc getchar
inline int read(){
    char ch=gc();
    int res=0,f=1;
    while(!isdigit(ch))f^=ch=='-',ch=gc();
    while(isdigit(ch))res=(res+(res<<2)<<1)+(ch^48),ch=gc();
    return f?res:-res;
}
#define ll long long
#define re register
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cs const
#define bg begin
template<class tp>inline void chemx(tp &a,tp b){a<b?a=b:0;}
template<class tp>inline void chemn(tp &a,tp b){a>b?a=b:0;}
int n,h;
double pw[73];
char s[10];
inline double ksm(double a,int b){
	double res=1;
	for(;b;b>>=1,a=a*a)if(b&1)res=res*a;
	return res;
}
int main(){
	scanf("%s",s+1);
	n=read(),h=read();
	if(s[1]=='A'){
		pw[0]=1;
		for(int i=1;i<=2*h;i++)pw[i]=pw[i-1]*0.5;
		double res=n;
		for(int i=1;i<=h;i++)
		for(int j=1;j<=n;j++)
		res+=1.0*(n-j)*ksm(1-pw[i],j-1)*pw[i*2]*((1<<i)-1.0*(1<<(i-1))*1.0*(1+1.0*(j-1)/((1<<i)-1)));
		printf("%.10f",res);
	}
	else cout<<n<<'
';
}

T3：

考试最后$15min$的时候推出来怎么做
如果考$5h$就可以写完了

考虑有$phi(ij)=phi(i)*phi(j)*frac{gcd(i,j)}{phi(gcd(i,j))}$

然后就可以枚举$gcd$乱莫反了

推出来最后就是
$ans=sum_{h}T(h)sum_{i,j}^{frac n h}phi(hi)phi(hj)dis(p[ih],p[jh])$
$p[i]$表示权值为$i$的点
$T(n)=sum_{d|n}frac{mu(frac n d)d}{phi(d)}$
然后随便虚树搞一下就完了
复杂度$O(nlog^2n)$

#include<bits/stdc++.h>
using namespace std;
const int RLEN=1<<20|1;
inline char gc(){
    static char ibuf[RLEN],*ib,*ob;
    (ob==ib)&&(ob=(ib=ibuf)+fread(ibuf,1,RLEN,stdin));
    return (ob==ib)?EOF:*ib++;
}
#define gc getchar
inline int read(){
    char ch=gc();
    int res=0,f=1;
    while(!isdigit(ch))f^=ch=='-',ch=gc();
    while(isdigit(ch))res=(res+(res<<2)<<1)+(ch^48),ch=gc();
    return f?res:-res;
}
#define ll long long
#define re register
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cs const
#define bg begin
template<class tp>inline void chemx(tp &a,tp b){a<b?a=b:0;}
template<class tp>inline void chemn(tp &a,tp b){a>b?a=b:0;}
cs int mod=1e9+7;
inline int add(int a,int b){return (a+=b)>=mod?a-mod:a;}
inline void Add(int &a,int b){(a+=b)>=mod?a-=mod:0;}
inline int dec(int a,int b){return (a-=b)<0?a+mod:a;}
inline void Dec(int &a,int b){(a-=b)<0?a+=mod:0;}
inline int mul(int a,int b){return 1ll*a*b%mod;}
inline void Mul(int &a,int b){a=1ll*a*b%mod;}
inline int ksm(int a,int b,int res=1){for(;b;b>>=1,Mul(a,a))(b&1)&&(Mul(res,a),1);return res;}
inline int Inv(int x){return ksm(x,mod-2);}
cs int N=200005;
int mu[N],phi[N],pr[N],T[N],tot;
bitset<N> vis;
int gcd(int a,int b){
	return b?gcd(b,a%b):a;
}
inline void init(){
	cs int len=N-5;
	mu[1]=phi[1]=1;
	for(int i=2;i<=len;i++){
		if(!vis[i])pr[++tot]=i,phi[i]=i-1,mu[i]=mod-1;
		for(int j=1;j<=tot&&i*pr[j]<=len;j++){
			vis[i*pr[j]]=1;
			if(i%pr[j]==0){phi[i*pr[j]]=phi[i]*pr[j];break;}
			phi[i*pr[j]]=phi[i]*phi[pr[j]],mu[i*pr[j]]=mod-mu[i];
		}
	}
	for(int i=1;i<=len;i++){
		int iv=Inv(phi[i]);
		for(int j=1;i*j<=len;j++)
		Add(T[i*j],mul(mul(mu[j],i),iv));
	}
}
int dep[N],fa[N],top[N],siz[N],son[N],in[N],out[N],dfn;
vector<int> e[N];
void dfs1(int u){
	siz[u]=1;
	for(int i=0;i<e[u].size();i++){
		int v=e[u][i];
		if(v==fa[u])continue;
		fa[v]=u,dep[v]=dep[u]+1;
		dfs1(v),siz[u]+=siz[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
}
void dfs2(int u,int tp){
	top[u]=tp,in[u]=++dfn;
	if(son[u])dfs2(son[u],tp);
	for(int i=0;i<e[u].size();i++){
		int v=e[u][i];
		if(v==fa[u]||v==son[u])continue;
		dfs2(v,v);
	}
	out[u]=dfn;
}
inline int Lca(int u,int v){
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		u=fa[top[u]];
	}
	return dep[u]<dep[v]?u:v;
}
inline int dis(int u,int v){
	return dep[u]+dep[v]-2*dep[Lca(u,v)];
}
int pos[N],a[N],n;;
namespace XS{
	vector<pii> e[N];
	int p[N],s[N],sum,tot,ans;
	int stk[N],top;
	inline bool comp(int a,int b){
		return in[a]<in[b];
	}
	inline void addedge(int u,int v){
		int d=dis(u,v);
		e[u].pb(pii(v,d));
	}
	void dfs(int u){
		for(pii &x:e[u]){
			int v=x.fi;
			dfs(v);
			Add(ans,mul(x.se,mul(dec(sum,s[v]),s[v])));
			Add(s[u],s[v]);
		}
	}
	void dfs2(int u){
		for(pii &x:e[u])
		dfs2(x.fi);
		s[u]=0,e[u].clear();
	}
	inline int calc(int x){
		top=tot=sum=ans=0;
		for(int i=1;i*x<=n;i++)p[++tot]=pos[i*x],Add(sum,phi[i*x]),s[p[tot]]=phi[i*x];
		sort(p+1,p+tot+1,comp);
		stk[++top]=p[1];
		for(int i=2;i<=tot;i++){
			int lca=Lca(stk[top],p[i]);
			while(in[lca]<in[stk[top]]){
				if(in[lca]>=in[stk[top-1]]){
					addedge(lca,stk[top--]);
					if(stk[top]!=lca)stk[++top]=lca;
					break;
				}
				addedge(stk[top-1],stk[top]),top--;
			}
			stk[++top]=p[i];
		}
		while(top>1)addedge(stk[top-1],stk[top]),top--;
		dfs(stk[1]),dfs2(stk[1]);
		return mul(ans,2);
	}
}
int main(){
	init();
	n=read();
	for(int i=1;i<=n;i++)a[i]=read(),pos[a[i]]=i;
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		e[u].pb(v),e[v].pb(u);
	}
	dfs1(1),dfs2(1,1);
	int res=0;
	for(int h=1;h<=n;h++){
		Add(res,mul(T[h],XS::calc(h)));
	}
	cout<<mul(res,Inv(mul(n,n-1)));
}