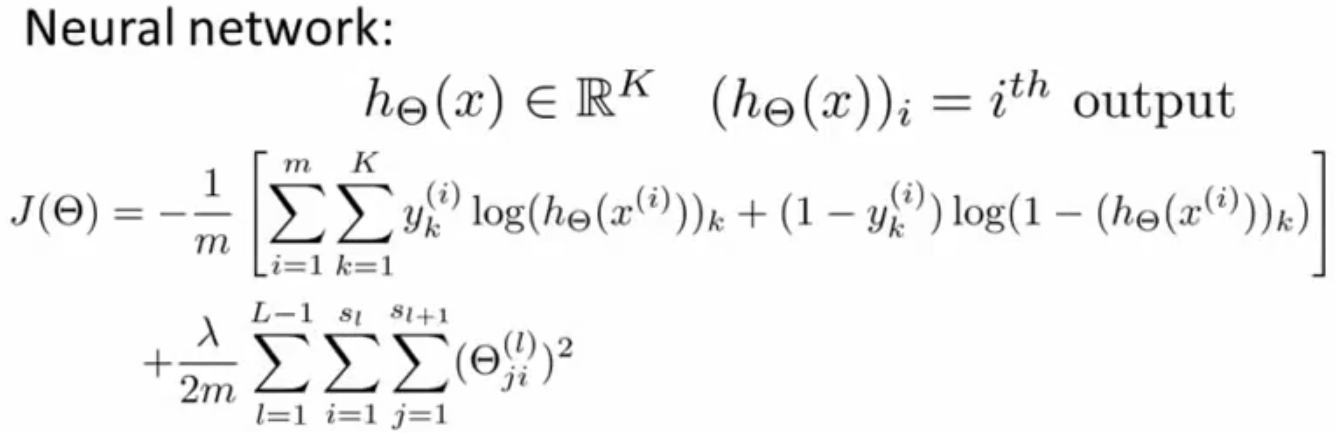机器学习之神经网络

前言

           以下内容是个人学习之后的感悟，转载请注明出处~

　　由于神经网络内容有点儿多，所以在此处建立以下目录，方便读者浏览。

• 简介
• 神经网络原理
• BP神经网络
• 梯度检验
• 参数随机初始化

简介

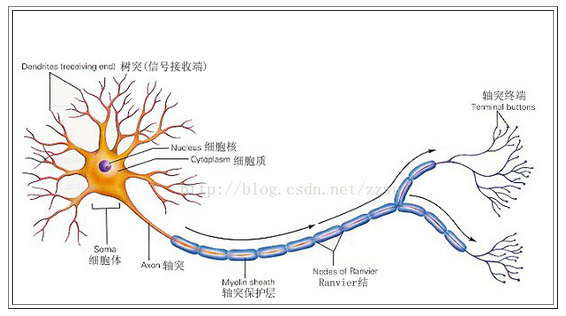
       神经细胞和人身上任何其他类型细胞十分不同，每个神经细胞都长着一根像电线一样的称为轴突（axon）的东西，它的

长度有时伸展到几厘米，用来将信号传递给其他的神经细胞。神经细胞的结构如下图所示。它由一个细胞体(soma)、一些树

突(dendrite) 、和一根可以很长的轴突组成。神经细胞体是一颗星状球形物，里面有一个核(nucleus)。树突由细胞体向各个

方向长出，本身可有分支，是用来接收信号的。轴突也有许多的分支。轴突通过分支的末梢(terminal)和其他神经细胞的树突

相接触,形成所谓的突触(Synapse), （图中未画出），一个神经细胞通过轴突和突触把产生的信号送到其他的神经细胞。

                                

　　正是由于数量巨大的连接，使得大脑具备难以置信的能力。尽管每一个神经细胞仅仅工作于大约100Hz的频率，但因各

个神经细胞都以独立处理单元的形式并行工作着，使人类的大脑具有下面这些非常明显的特点：

• 能实现无监督的学习
• 对损伤有冗余性(tolerance)
• 处理信息的效率极高
• 善于归纳推广
• 它是有意识的

　　因此，一个人工神经网络( Artificial neural network, ANN）简称神经网络（NN)， 就是要在当代数字计算机现有规模的

约束下，来模拟这种大量的并行性, 并在实现这一工作时，使它能显示许多和人或动物大脑相类似的特性。

神经网络原理

　　神经网络是一种非线性学习算法，神经网络中最基本的成分是神经元（neuron），下面给出神经元的基本模型：

 　　　                                 　

　　

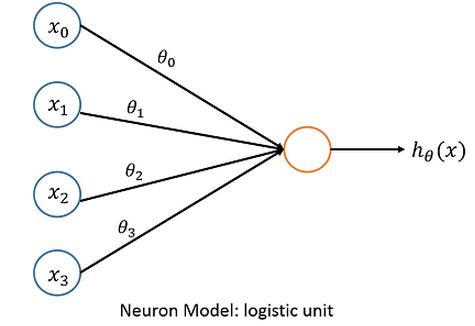
　　进入人工神经细胞的每一个样本特征x_i都与一个权重θ相乘，作为图中橘色大圆的输入。橘色大圆的“核”是一个激励函数，

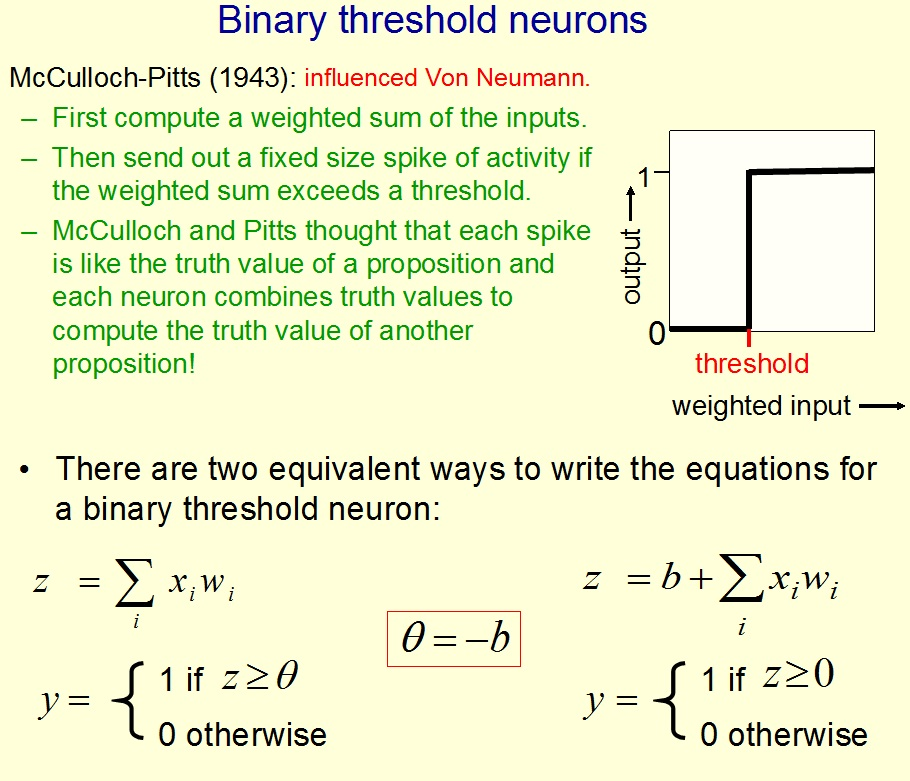
它把所有这些新的、经过权重调整后的输入全部加起来，形成单个的激励值。然后，激励函数根据激励值产生输出。激励函数有

好多种类型，常见的有以下几种：

 

 

  

 

　　介绍完神经元的基本模型，接下来介绍的是神经网络的基本模型：

                                         

　　上图中并未画出x₀和a₀，其值一般取+1，θ₁₀⁽¹⁾和θ₂₀⁽²⁾分别是它们的权值。上图中的三个层次分别是输入层、隐藏层、输

出层，其实现的整个过程如下列公式所示（其中g()即为激励函数）：

                                                                    

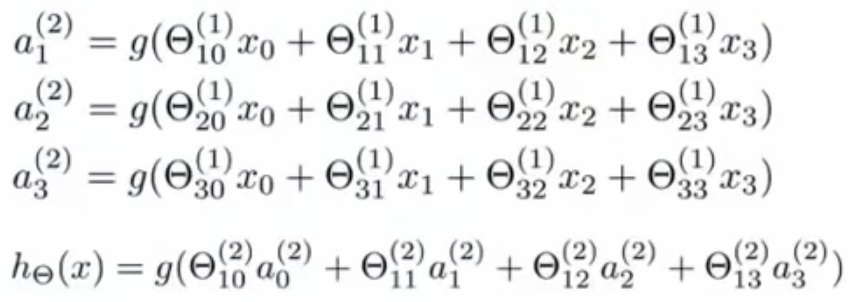
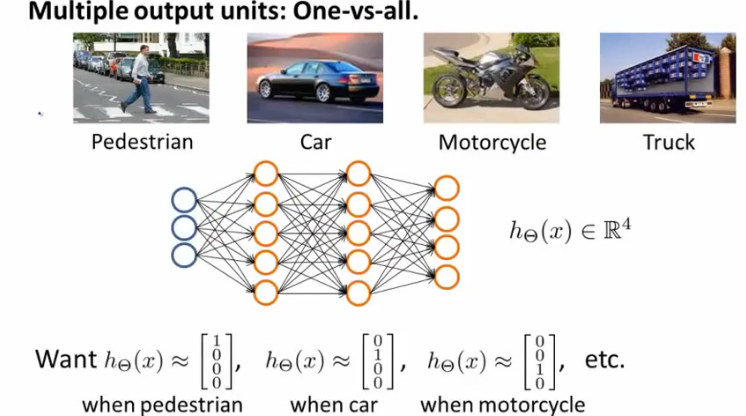
　　一般在分类应用中，需要分很多类别，那么，神经网络在多分类应用中又是怎么实现的呢？看下图，我们可以清晰地看到，采

用二进制编码式的形式，可以完美地解决这个问题。

                   

　　那么又是如何求出这些权重值得呢，其实学过线性回归、逻辑回归的童鞋应该知道，对~，使用代价函数。但是神经网络的激

励函数不同，其代价函数也有所不同，为了方便起见，此处与下文的激励函数全部取为S型函数。神经网络的代价函数如下，由于

此处采用的是S型函数，是否会觉得其形式有点像逻辑回归的代价函数呢？（本人看了一下，正则项还是区别很大的~）

                                      

BP神经网络

　　BP（Back Propagation）神经网络是目前神经网络领域最成功的算法之一。它是一种按误差逆传播算法训练的多层前馈网络，

能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。

　　BP算法可以求出最佳权值，下面来看看BP算法的基本原理。首先，利用前向传播算法求出各层的激励值，如下图所示：

　　接下来看BP算法：定义为第L层单元i的残差。BP算法的目标是最小化J(θ)。而对于样例来说，其均方误差为：

                                                                      

　　在梯度下降中，每一次迭代都按如下公式对参数更新：

                                                              ，

　　BP算法的思路如下：给定一个样例，先根据前向传导（forward propagation）计算出神经网络中的所有激活值。针

对第层的每一个节点i，我们可以计算出其“残差”，该残差表明了该节点对最终输出值的残差产生了多少影响。其实可以直白的

理解为：令，为了计算的方便，因为算每一层的权重梯度都要依赖后一层，以此类推。对于最后一层输出层，我们可以直

接计算出神经网络的输出与实际类别值之间的残差。那么重点是对于隐藏层该如何处理？我们将基于节点第层的残差的加权平

均值计算出，这些节点以作为输入。

因此，对于最后一层输出层L(用L表示最后一层输出层)来说：

对于隐藏层来说：

因此可得：

                     

这样，我们就可以求得偏导数：，    。

关于BP算法的公式推导已经介绍完了，大家可以自己在纸上推导一下。下面来总结一下，BP算法的执行过程：

                         

以上就是BP算法的细节原理。概括来讲就是：

1、利用forward propagation计算出每一层的“激活值”。

2、计算出最后一层即输出层每个输出单元的残差。

3、计算出第层节点的残差。

4、计算出我们需要的偏导数。

如果用向量化描述以上步骤，则为：

1、利用前向传导计算各层的“激活值”。

2、对于输出层，计算：

3、对于其他各层，计算：

4、计算最终的导数值：

最终得到更新权重的公式： 。

注：在实际应用中有个注意点：

讲了这么多，大家来看看例子，可行更加形象化的让大家体会下BP算法的执行过程细节：

                           

 

 

梯度检验

　　BP算法细节繁多，而且甚是复杂，有可能出现梯度消失或爆炸的现象，因此非常容易出错，很难检查出来。如下图所示，

当w值全都大于1，或者全都小于1，那么下面的多层网络的输出值将会很大或者很小。

                               

　　因此需要使用梯度检验，梯度检验能够非常的确信的检验你实现的BP算法是否正确。梯度检验如下图所示：

                             

因此，对于每个参数使用梯度检验：

                         

　　因为在BP算法执行过程中，我们就可以将这个近似值与的导数相比较，如果两者相同或者非常接近，则可以确认我们实现的

BP算法是正确的。有个注意点：当你训练BP神经网络时，一定要关闭gradient checking，因为梯度检验的执行速度非常非常慢。

 

参数随机初始化

　　我们在线性回归和logistic回归中都可以把初始化为zeros(n,1)，这样做是可以的。但是在神经网络中这样做却是不可以的，因为如

果初始化的参数一样，意味着隐藏层的每个单元的输入权重是一样的，因此每次更新后隐藏层的单元值将会是一样的。这就意味着所有的

隐藏层单元都在计算相同的特征，这是完全多余的。来个图形象化的理解一下：

                          

因为在神经网络参数（权重）初始化的时候，需要随机初始化，就是把的值随机初始化，范围为。

 

注：按经验来说，可以采用如下方法（其中shape为权重参数矩阵的大小）：

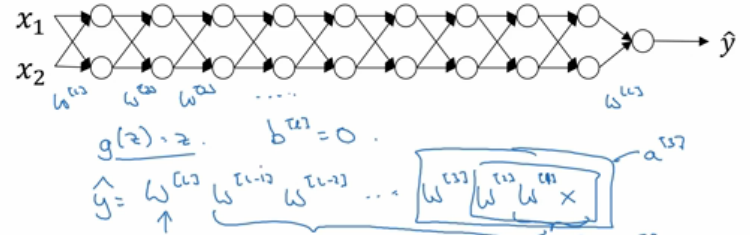
• 激活函数：Relu    

                                     

• 激活函数：tanh

                                    

 

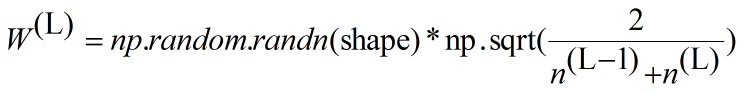
以上是全部内容，如果有什么地方不对，请在下面留言，谢谢~