支持向量机是一个比较经典分类算法,这几天死磕了一下支持向量机,手推了一下相应的算法,特此做一个笔记。
1、线性可分SVM
线性可分的支持向量机就是给定相应的数据集,这个数据集可以用一个超平面,将正例和负例进行分类。且这个超平面尽可能远的分割正例和负例,如下图所示。
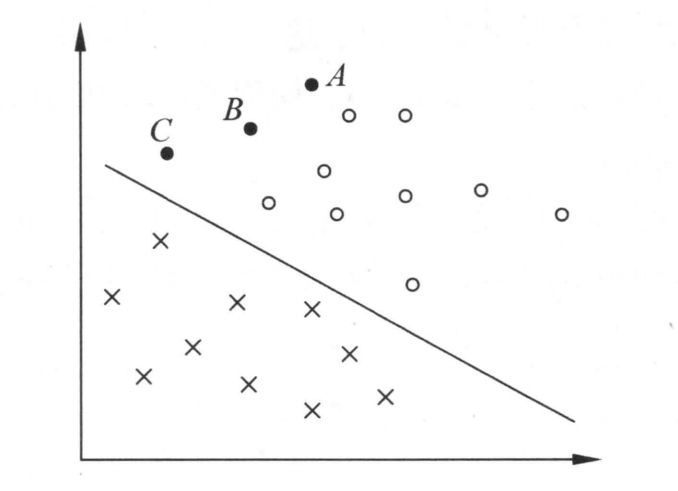
如果我们能找到一个超平面,假定是(wx+b=0) ,然后我们外层套一个函数(f(x)=sign(wx+b)),即
[ f(x) = left {
�egin{array}{**lr**}
+1, ; if x >= 0 & \
-1, ; if x < 0
end{array}
ight.
]
也就是说,如果我们算出了(w,b)这两个变量,那么我们直接将未知的数据扔到(wx+b)里,如果这个值大于等于0,可以归为+1类,如果值小于0,可以归为-1类。
那么,根据前面的讲述,我们的问题就是如何求出参数(w,b)了,这里,我们设定任意一个数据((x_{i},y_{i}))到这条超平面的距离为
[ gamma_{i} = frac {|wx_{i} + b| } {left|w
ight|_2}
]
上述是点到直线的距离公式,由于分子是带有绝对值的,后续优化会比较的麻烦,所以我们想办法,将绝对值符号去掉,如何去掉呢?我们可以利用(y_{i})这个值,如果(wx_{i} + b)为正,那么(y_{i}(wx_{i} + b))为正,同样,如果(wx_{i} + b)为负,那么(y_{i}(wx_{i} + b))也为正,所以,我们可以用(y_{i}(wx_{i} + b))来代替(|wx_{i} + b|),重新更新一下
[ gamma_{i} = frac { y_{i}(wx_{i} + b) } {left|w
ight|_2} \
令y_{i}(wx_{i} + b) = ilde{gamma_{i}} ; 则原式等于 \
gamma_{i} = frac { ilde{gamma_{i}} } {left|w
ight|_2}
]
其中(gamma_{i})称为几何距离,( ilde{gamma_{i}})称为函数距离。由于我们要最大化数据集最近的点到直线的距离,所以,我们期望最近的点到直线的距离最大,那我们定义最近的点为
[ gamma = min_{i=1,2...n} gamma_{i}
]
这样,我们最大化这个(gamma)就可以了,这里,我们假定(gamma)所对应的点的函数间隔为1,即该点(y_{i}(wx_{i} + b = 1),这个点可以随便定,因为满足这个超平面的的直线方程(wx + b = 0)有无数个,因为我们同时增大(w,b),这个直线没有变,所以我们这里假定这个值为1,主要是为了方便优化。这里也可以这样理解,我们可以设定不同的值,比如设定为0.5,那么我们最后得到的(w,b)也变为之前的一半,所以这里定为几都没有影响。
所以,如果我们的优化方式可以这样写
[ max frac{ ilde{gamma} }{ left|w
ight|_2 } \
s.t ; y_{i}(wx_{i} + b >= ilde{gamma} ; i=1,2,3....n
]
如上讨论,我们假定( ilde{gamma} = 1),所以上述式子转化为
[ max frac{ 1 }{ left|w
ight|_2 } \
s.t ; y_{i}(wx_{i} + b >= 1 ; i=1,2,3....n
]
进而,我们将求最大变换为求最小
[ min frac{ 1 }{ 2} {left|w
ight|_2}^2 \
s.t ; y_{i}(wx_{i} + b >= 1 ; i=1,2,3....n ag{1}
]
这样,我们的优化条件就写完了,我们的目的是得到上述式子的(w,b)的值,那怎么求呢?由于式子(1)是一个凸优化问题,则可以引入拉格朗日乘子,进行求解
[ L(w,b,alpha) = frac{ 1 }{ 2} {left|w
ight|_2}^2 - sumlimits_{i=1}^{N} alpha_{i} y_{i}(w * x_{i} + b) + sumlimits_{i=1}^{N} alpha_{i}
]
由此,我们得到
[ min_{w,b} max_{alpha} L(w,b,alpha) ag{2}
]
有对偶性我们可以得到
[ max_{alpha} min_{w,b} L(w,b,alpha) ag{3}
]
我们令式子(2)的最优解为(p^{*}),令式子(3)的最优解为(d^{*}),有(d^{*} <= p^{*}),那什么时候两者相等,且原始问题的解是对偶问题的解呢?满足:(frac{ 1 }{ 2} {left|w
ight|_2}^2)和(1 - y_{i}(wx_{i} + b)这两个函数是凸函数,且存在(w,b),对任意的(i)来说,满足(1 - y_{i}(wx_{i} + b < 0)。可以发现,咱们的公式满足上述条件。所以原始问题和对偶问题的解是一样的,则我们将原始问题转为对偶问题。
分别对(w,b)进行求导,可以得到
[ frac{partial L(w,b,alpha) }{ partial w} = w - sumlimits_{i=1}^{N} alpha_{i}y_{i}x_{i} \
frac{partial L(w,b,alpha) }{ partial b} = - sumlimits_{i=1}^{N} alpha_{i} y_{i}
]
令上述的求导等于0,可以得到
[ w = sumlimits_{i=1}^{N} alpha_{i}y_{i}x_{i} \
sumlimits_{i=1}^{N} alpha_{i} y_{i} = 0
]
将结果带入到(L(w,b,alpha))公式中,得到
[ max_{alpha} - frac{1}{2} sumlimits_{i=1}^{N} sumlimits_{j=1}^{N} alpha_{i}alpha_{j} y_{i}y_{j}x_{i}x_{j} + sumlimits_{j=1}^{N} alpha_{i} \
等价于 min_{alpha} frac{1}{2} sumlimits_{i=1}^{N} sumlimits_{j=1}^{N} alpha_{i}alpha_{j} y_{i}y_{j}x_{i}x_{j} - sumlimits_{j=1}^{N} alpha_{i}
]
假如我们求解出$alpha^{ * } = (alpha_{1}^{ * } , alpha_{2}^{ * }, ......alpha_{N}^{ * }) $,(这里求解方法见SMO算法)将结果带入原公式,可以得到
[ w = sumlimits_{i=1}^{N} alpha_{i}^{*} y_{i}x_{i}
]
既然(w)求解出来了,那么(b)怎么求解呢?我们可以利用KKT条件,根据KKT条件,我们得到
[ alpha_{i}^{*} (y_{i}(w_{i}^{*} * x_{i} + b^{*}) - 1) = 0 \
y_{i}(w_{i}^{*} * x_{i} + b^{*}) - 1 >= 0 \
alpha_{i}^{*} >= 0 \
其中 i = 1,2,3.....N
]
由于必定存在一个(alpha_{i}^{*} >0)所以针对这个$ alpha_{i}^{*} (可以得到) y_{i}(w_{i}^{ * } x_{i} + b^{ * }) - 1 = 0 $,则
[ b^{*} = y_{i} - sumlimits_{j=1}^{N} alpha_{j}^{*} y_{j} x_{j} x_{i}
]
至此,我们完成了第一部分的讲解。
2、线性不可分SVM
以上我们介绍的是线性可分的,但是对于大部分数据来说,并不是线性可分的,会有一些异常点,如果我们把异常点也算作正常的点的话,那么最终的模型会效果会不好。那么对于线性不可分的数据点来说,可以加入一个松弛变量(xi),之后我们的约束条件变成
[ min frac{ 1 }{ 2} {left|w
ight|_2}^2 + C sumlimits_{i=1}^{N} xi_{i} \
s.t ; y_{i}(wx_{i} + b >= 1 - xi_{i} ; i=1,2,3....n \
; xi_{i} >= 0 ; i=1,2,3....n
]
首先引入拉格朗日乘子,得到原始的优化问题
[ L(w,b,xi ,alpha,mu) = frac{ 1 }{ 2} {left|w
ight|_2}^2 + C sumlimits_{i=1}^{N} xi_{i} + sumlimits_{i=1}^{N} alpha_{i} (1-xi_{i}-y_{i}(wx_{i} + b)) + sumlimits_{i=1}^{N} (- xi_{i} mu_{i}) \
原始问题是 min_{w,b,xi} max_{alpha,mu} L(w,b,xi ,alpha,mu) \
对偶问题是 max_{alpha,mu} min_{w,b,xi} L(w,b,xi ,alpha,mu)
]
我们首先求解(min_{w,b,xi} L(w,b,xi ,alpha,mu)),分别对(w,b,xi)求导为
[ frac {partial L(w,b,xi ,alpha,mu)}{ partial w} = w - sumlimits_{i=1}^{N} alpha_{i} y_{i} x_{i} \
frac {partial L(w,b,xi ,alpha,mu)}{ partial b} = - sumlimits_{i=1}^{N} alpha_{i} y_{i} \
frac {partial L(w,b,xi ,alpha,mu)}{ partial xi} = C - alpha_{i} - mu_{i} \
]
分别令上述各式子等于0,并将相应的结果带入原公式,得到
[ min_{alpha} frac{1}{2} sumlimits_{i=1}^{N} sumlimits_{j=1}^{N} alpha_{i}alpha_{j}y_{i}y_{j}x_{i}x_{j} \
s.t sumlimits_{i=1}^{N}alpha_{i}y_{i} = 0 \
0<= alpha_{i} <= C ;;;; 根据C-alpha_{i} - mu_{i} = 0 和 alpha_{i} >=0 和 mu_{i} >= 0得出
]
设(a^{*})是上述问题的解,那么我们最终得到
[ w^{*} = sumlimits_{i=1}^{N} alpha_{i}^{*} y_{i} x_{i} \
b^{*} = y_{j} - sumlimits_{i=1}^{N} y_{i}alpha_{i}^{*} (x_{i} * x_{j})
]
(w^{*})这里我们就不讲了,至于这个(b^{*}),可以知道,原求解中必然含有一个(alpha_{j}),使(0<alpha_{i} < C),那么根据KKT条件,(alpha_{i}>0)会使(1-xi_{i}^{*}-y_{i}(w^{*}x_{i} + b) = 0),(alpha_{i} < C)会得出(mu_{j} != 0)则(xi_{i} = 0),则可以得到原公式。从数学上如何理解呢?(alpha_{i}>0)表明所在的点目前是在支撑向量上,处在支撑向量上的点自然(xi_{i}=0)了,因为这里没有分类错误,所以没有惩罚。那为何线性不可分的解和线性可分的解一样呢?其实,公式虽然一样,但是求得的(alpha^{*})是不一样的,因为线性可分的约束条件是$a_{i} >= 0 $但是线性不可分的约束条件是(0=<alpha_{i} =< C)
3、非线性SVM
对于非线性的SVM来说,我们需要将原始的x映射到高维的(phi (x)),进而进行求解。这个函数我们可以自己定义,但是有一个问题是当问题比较复杂的时候,这个函数会得到维度非常大的向量,接着再和同样维度的向量进行向量内积操作,虽然这种方法理论上是可行的,但是实际中时间耗费较长,所以提出了核技巧,就是根据一个函数,所有的计算都在低纬度进行,同样可以达到映射到高纬度的效果。
4、SMO算法
SMO算法又叫做序列最小最优化算法,这个算法可以求解上面的(alpha),下面就介绍这种算法。假设我们的数据集是非线性的数据集,则关于(alpha)的优化公式如下所示
[ min_{alpha} frac {1}{2}sumlimits_{i=1}^{N} sumlimits_{j=1}^{N} alpha_{i}alpha_{j} y_{i}y_{j}K(x_{i},x_{j}) - sumlimits_{i=1}^{N} alpha_{i} \
s.t ;;;;; sumlimits_{i=1}^{N} y_{i}alpha_{i} = 0 \
0 <= alpha_{i} <= C ;;;;; i=1,2,3,.....N
]
其中,优化的思想是这样的,首先,我们选择两个变量(alpha_{1},alpha_{2}),然后固定其他的(alpha),只对这两个变量进行优化。这种优化思想之所以可以成立,其思想是这样的,假如所有的(alpha)都符合相应的KKT条件,那么这一组解就可以作为结果输出,否则,我们必然可以找到两个(alpha),固定这两个(alpha)使这两个变量构成的二次规划问题更接近原始问题的解。这里我有一个疑问,如果我们只选择一个不符合要求的a可以吗?。所以,我们的问题有两个:1、如何选择这两个(alpha),2、选择了之后如何进行优化求解。首先我们先来解决第二个问题,假设我们得到了两个变量(alpha_{1},alpha_{2}),那么优化这两个变量,固定其他变量,可以得到
[ L(alpha_{1},alpha_{2}) = frac{1}{2} alpha_{1}^{2}K_{11} + frac{1}{2} alpha_{2}^{2}K_{22} + alpha_{1}alpha_{2}y_{1}y_{2}K_{12} - alpha_{1} - alpha_{2} + alpha_{1}y_{1}v_{1} + alpha_{2}y_{2}v_{2} \
其中K_{ij} = K(x_{i},x_{j}) \
v_{1} = sumlimits_{i=3}^{N}alpha_{i}y_{i}k_{i1} \
v_{2} = sumlimits_{i=3}^{N}alpha_{i}y_{i}k_{i2} \
这里的限制条件是alpha_{1}y_{1} + alpha_{2}y_{2} = - sumlimits_{i=3}^{N}alpha_{i}y_{i} = S \
0 <= alpha_{i} <= C ;;;;; i=1,2,3,.....N
]
这里,我们可以将(alpha_{1})用(alpha_{2})表示,进而将(alpha_{1})带入,变成只有一个变量(alpha_{2})的公式,进而对原公式进行求导,等于0后,得到(alpha_{2})的解,进而得到(alpha_{1})的解,进而进行更新。根据公式我们得到(alpha_{1} = (S - alpha_{2} y_{2})y_{1}),因为(y_{1} * y_{1} = 1)。带入公式得到
[ L(alpha_{2}) = frac {1}{2} (S - alpha_{2}y_{2}) ^ {2} K_{11} + frac{1}{2} alpha_{2}^{2}K_{22} + y_{2}K_{12} (S - alpha_{2} y_{2})alpha_{2} - (S - alpha_{2}y_{2})y_{1} - alpha_{2} + v_{1}(S - alpha_{2}y_{2}) + y_{2}v_{2} alpha_{2}
]
对(alpha_{2})求导,得到
[ frac {partial L(alpha_{2})} {alpha_{2}} = K_{11}alpha_{2} + K_{22}alpha_{2} - 2 K_{12}alpha_{2} + K_{11}Sy_{2} + K_{12}Sy_{2} + y_{1}y_{2} - 1 -v_{1}y_{2} + y_{2}v_{2}
]
令上述式子等于0,可以得到
[ alpha_{2} = frac {y_{2} (K_{11}S - K_{12}S - y_{1} + v_{1} - v_{2} + y_{2})} {K_{11} + K_{22} - 2K_{12}}
]
这里我们就得到了(alpha_{2})了,但是这个式子有些长,我们对他进行一些优化,首先,我们令
[ E_{i} = g(x_{i}) - y_{i} = ( sumlimits_{j=1}^{N} alpha_{j}y_{j}K(x_{j},x_{i}) + b) - y_{i}
]
上述式子的含义是预测的结果和现实结果的差值。那么(v_{i})则可以表示为
[ v_{i} = g(x_{i}) - sumlimits_{j=1}^{2} alpha_{j}y_{j}K(x_{j},x_{i}) - b
]
则结果为
[ alpha_{2} = frac { y_{2} [ y_{2} - y_{1} + K_{11}S - K_{12}S + (g(x_{1}) - sumlimits_{j=1}^{2} alpha_{j}y_{j}K(x_{j},x_{1}) - b) - (g(x_{2}) - sumlimits_{j=1}^{2} alpha_{j}y_{j}K(x_{j},x_{2}) - b) ] } {K_{11} + K_{22} - 2K_{12}}
]
将(S = alpha_{1}^{old} y_{1} + alpha_{2}^{old}y_{2})带入上式,得到
[ alpha_{2}^{new,unc} = alpha_{2}^{old} + frac {y_{2} (E_{1} - E_{2}) } { K_{11} + K_{22} - 2K_{12} }
]
这个是未经剪辑的(alpha_{2})的结果,(alpha_{2}^{new,unc})还有一些限制条件,这里根据公式
[ S = alpha_{1}y_{1} + alpha_{2}y_{2} \
0 <= alpha_{i} <= C
]
可以得到(alpha)的最大值和最小值,经过化简得到
[ 0 <= -y_{1}y_{2} alpha_{2} + Sy_{2} <= C \
-Sy_{2} <= alpha_{2} <= C - Sy_{2} ;;;;; 当y_{1} 和y_{2}符号不同时 \
Sy_{2} - C <= alpha_{2} <= Sy_{2} ;;;;; 当y_{1} 和y_{2}符号相同时
]
则
[ max {-Sy_{2}, Sy_{2} - C, 0} <= alpha_{2} <= min{C - Sy_{2}, Sy_{2} , C}
]
有了这个式子的约束,我们就能得到最终的结果(alpha_{2}),而(alpha_{1})可以根据公式(S=alpha_{2}y_{2} + alpha_{1}y_{1}).
我们还有一个问题是如何选择这两个(alpha),这里可以根据这样的标准,第一个(alpha_{1})可以根据如果其不满足KKT条件,第二个(alpha_{2})可以根据约束条件获得,更具体来说,(alpha_{1})的选择方法是
[ g(x_{i}) * y_{i} >= 1 时, alpha_{i} > 0是不满足的,理论上应该alpha_{i} = 0 \
g(x_{i}) * y_{i} = 1 时, alpha_{i} = 0 或者alpha_{i} = C是不满足的,理论上是 0 < alpha_{i} < C \
g(x_{i}) * y_{i} <= 1 时, alpha_{i} < C 是不满足的,理论上是alpha_{i} = C
]
根据这些不满足条件的情况,选择第一个(alpha_{1}),对于第二个(alpha_{2})可以通过(|E_{1} - E{2}|)得到最大这个式子值的(alpha_{2})得到第二个(alpha_{2}).
