zoukankan      html  css  js  c++  java

  • 笔记整理--算法

    也谈哈希表 - LukyW - 博客园 - Google Chrome (2013/11/24 9:32:55)

    也谈哈希表

     

    基本概念

    　　哈希表（Hash Table）是一种根据关键字直接访问内存存储位置的数据结构。通过哈希表，数据元素的存放位置和数据元素的关键字之间建立起某种对应关系，建立这种对应关系的函数称为哈希函数（如图）。

    哈希函数构造方法

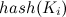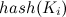    　　哈希表的构造方法是：假设要存储的数据元素个数为n，设置一个长度为m（m≥n）的连续存储单元，分别以每个数据元素的关键字为自变量，通过哈希函数，把映射为内存单元的某个地址，并将该数据元素存储在该内存单元中。

    　　从数学的角度来看，哈希函数实际上是关键字到内存单元的映射，因此我们希望通过哈希函数通过尽量简单的运算使得通过哈希函数计算出的哈希地址尽量均匀地被映射到一系列的内存单元中。构造哈希函数有三个要点：第一，运算过程要尽量简单高效，以提高哈希表的插入和检索效率；第二，哈希函数应该具有较好的散列性，以降低哈希冲突的概率；第三，哈希函数应具有较大的压缩性，以节省内存。一般有以下几种常见的方法：

    1. 直接定址法，该方法是曲关键字的某个线性函数值为哈希地址。可以简单的表示为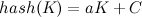：，优点是不会产生冲突，但缺点空间复杂度可能会很高，适用于元素较少的情况下；
    2. 除留余数法，它是用数据元素关键字除以某个常数所得的余数作为哈希地址，该方法计算简单，适用范围广，是最经常使用的一种哈希函数，可以表示为：，该方法的关键是常数的选取，一般要求是接近或等于哈希表本身的长度，理论研究表明，该常数取素数时效果最好。
    3. 数字分析法：该方法是取数据元素关键字中某些取值较均匀的数字位来作为哈希地址的方法，这样可以尽量避免冲突，但是该方法只适合于所有关键字已知的情况。对于想要设计出更加通用的哈希表并不适用。

    哈希冲突解决办法

    　　在构造哈希表时，存在这样的问题，对于两个不同的关键字，通过我们的哈希函数计算哈希地址时却得到了相同的哈希地址，我们将这种现象称为哈希冲突（如图）:

    　　哈希冲突主要与两个因素相关：第一，填装因子，所谓的填装因子是指哈希表中已存入的数据元素个数与哈希地址空间大小的比值，即α=n/m，α越小，冲突的可能性就越小，相反则冲突可能性越大；但是α越小，哈希表的存储空间利用率也就很低，α越大，存储空间的利用率也就越高，为了兼顾哈希冲突和存储空间利用率，通常将α控制在0.6-0.9之间，而.NET中的Hashtable则直接将α的最大值定义为0.72（注：虽然微软官方MSDN中声明Hashtable默认填装因子为1.0，事实上所有的填装因子都为0.72的倍数）；第二，与所用的哈希函数有关，如果哈希函数选择得当，就可以使哈希地址尽可能的均匀分布在哈希地址空间上，从而减少冲突的产生，但一个良好的哈希函数的得来很大程度上取决于大量的实践，不过幸好前人已经总结实践了很多高效的哈希函数，可以参考园子里大牛Lucifer的文章：数据结构 : Hash Table [I]。

    　　哈希冲突通常是很难避免的，解决哈希冲突有很多种方法，通常分为两大类：

    1. 开放定址法，它是一类以发生哈希冲突的哈希地址为自变量，通过某种哈希函数得到一个新的空闲内存单元地址的方法（如图），开放定址法的哈希冲突函数通常是一组；
    2. 链表法，当未发生冲突时，则直接存放该数据元素；当冲突产生时，把产生冲突的数据元素另外存放在单链表中。

    Hashtable和Dictionary

    　　.NET中实现了哈希表的类分别是Hashtable和Dictionary<TKey, TValue>，Hashtable由包含集合元素的存储桶组成，存储桶是Hashtable中各元素的虚拟子组，与大多数集合中进行的搜索相比，存储桶可使搜索更为便捷。Dictionary则是泛型版本的哈希表，与Hashtable的功能相同，对于值类型，特定类型（不包括Object）的性能优先于Hashtable，这是因为Hashtable的元素属于Object类型，所以在存储或者检索类型时通常发生装箱和拆箱操作；除此之外，虽然微软宣称Hashtable是线程安全的，可以允许多个读线程或一个写线程访问，但是事实是它也并非线程安全，在.NET Framework 2.0新引入的Dictionary仍旧为解决这个问题，其中限于公共静态方法是线程安全的，因此可以说Dictionary是非线程安全的，而且对整个集合的枚举过程对二者而言都不是线程安全的，因为当出现枚举与写访问互相争用这种情况发生时，则必须在整个枚举过程中对整个集合加锁。如果我们在使用.NET Framework 4.0以上版本，我们可以使用线程安全的ConcurrentDictionary；另一个比较重要的区别在于，虽然它们都实现了哈希表，但是二者却使用了完全不同的哈希冲突解决方法，Hashtable解决冲突的方式是开放定址法，而Dictionary则采用了链表法。

    Hashtable的实现原理

    　　Hashtable类中哈希函数的定义可以用如下递推公式来表示：

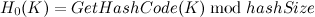
    通过简单的数学推导就可以得出其通项式公式即Hashtable的哈希函数簇为：

    因此我们就拥有了一系列的哈希函数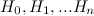：，当我们向哈希表中增加元素时，则依次尝试使用这些哈希函数，直到找到相应的空闲内存单元地址为止，这种方式称为二度哈希。

    　　在Hashtable类中，包含元素的存储桶被定义在结构体bucket中：

    1 private struct bucket
2 {
3     public object key;
4     public object val;
5     public int hash_coll;
6 }

    其中前两个字段很容易理解，分别代表了哈希表中的关键字和值，对于第三个字段hash_coll，实际上保存了两种信息：关键字的哈希码和是否冲突，coll为collision（冲突）的缩写，该字段为32位整型类型，最高位为符号位，当最高位为0时，表示该数为正数，表示未发生冲突，为1时为负数，表示发生了冲突，剩下的其他位则用于保存哈希码。

    　　下面我们来看一个简单的哈希表元素增删过程，使得我们对于哈希表的具体工作方式有一个更直观的了解，当我们未指定具体Hashtable容量大小时，来进行一组数据的插入操作，此时Hashtable类会自动初始化其容量为默认最小值3。

    1. 插入元素[20, “elem1”]，根据Hashtable类哈希函数通项式，所以其哈希代码的值为，此时为第一次插入数据，因此不存在冲突，直接寻址到bucket[2]，由于不存在冲突，因此hash_coll的值即为其key的哈希代码，存储结构如下图：
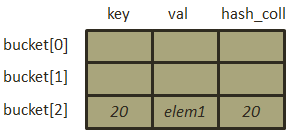
    2. 插入元素[33, “elem2”]，同理，此时仍然不存在冲突，存储结构如下：
    3. 插入元素[40, “elem3”]，此时的哈希表进行扩容，为什么会在此时扩容呢，哈希表的填装因子为2/3=0.66并未超过0.72，在.NET中，微软对填装因子进行了换算，通过填装因子与哈希表大小的乘积取整获得哈希表的最佳填装量即：3×0.72=2。扩容后的哈希表大小为原表容量大小的2倍后的质数，在本例中再次扩容后哈希表大小为7。进行扩容之后，原哈希表的已经存储的元素必须按照新的哈希表的哈希函数（其实哈希函数本身没有发生变动，发生变动的是哈希表的长度）进行计算，重新寻址，扩容后的哈希表如下：

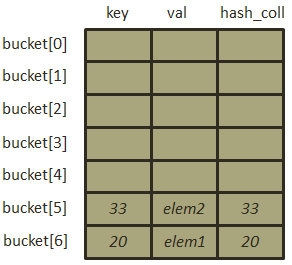
      完成扩容过程后才会对[40, “elem3”]进行插入操作，，现在我们发现冲突产生了，因为此时bucket[5]的位置已经有元素了，此时进行二度哈希：
                 
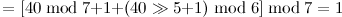
      此时哈希表中位置为1的空间仍旧处于空闲状态，因此进行插入操作，在将元素插入之前，由于bucket[5]出现了冲突，因此需要对其进行标记，将hash_coll的最高位置为1，表示其出现了冲突，所以完成插入后哈希表结构如下图：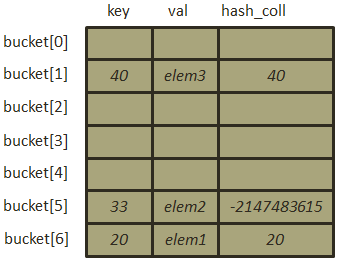
    4. 插入元素[55, “elem4”]，同理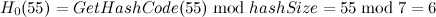，，产生冲突，进行二度哈希：

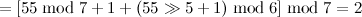      ，完成插入后哈希表的存储结构为：
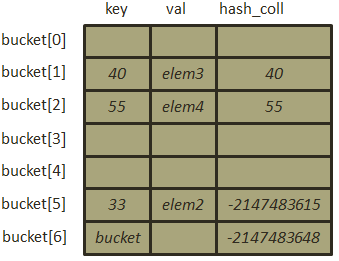
    5. 删除元素[20, “elem1”]，在删除元素时，同样需要根据哈希函数来进行寻址，如果有冲突，则进行二度哈希，但是值得注意的一点是，删除冲突标记元素（即元素的hash_coll值为负数）和非冲突标记元素是有差别的，在删除非冲突标记元素时，则直接将要删除的元素的键和值修改为null并将hash_coll置0即可，但是在删除冲突标记元素时，需将hash_coll的hash部分（即0-30位）置0以及将元素的值置为null，还需将该元素的键指向整个哈希表，之所以这样做是因为当索引为0的元素也出现冲突时，将无法判断该位置是一个空位还是非空位，那么再次进行插入时很可能将索引为0处的元素覆盖。删除[20， “elem1”]后的结构为：

    Dictionary的实现原理

    　　从.NET Framework 2.0开始，随着泛型的引入，类库提供一个新的命名空间System.Collection.Generic，并且在该命名空间下新增了Dictionary等泛型类。

    　　Dictionary的哈希函数就相对简单，就是简单的除留余数法，对于冲突解决，Dictionary则采用了链表法，但是此时buckets数组已经退化为专门用于存储元素的位置（下标）的整型数组，包含元素的数据结构被定义为结构体Entry，通过一个Entry类型的数组entries专门用于存储元素，Entry的定义如下：

    复制代码
    1 private struct Entry
2 {
3     public int hashCode;
4     public int next;
5     public TKey key;
6     public TValue value;
7 }
    复制代码

    其中的next字段表示数组链表的下一个元素的下标，一个关于数据存储结构的简单图示如下：

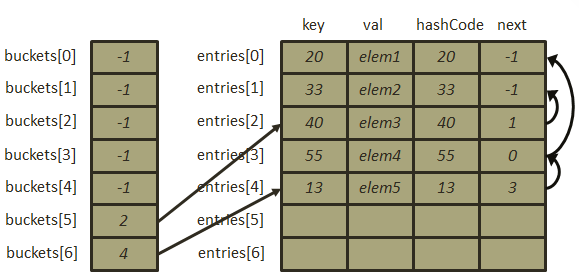
    我们用同样的方式来看看Dictionary插入和删除元素的简单过程：

    1. 插入元素[20, “elem1”]，跟Hashtable类似，Dictionary初始化容量也为3（如果未指定初始化容量），Dictionary的哈希函数就非常简单了，除留余数法直接获取其哈希地址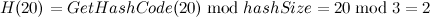，，那么此时在entries[0]直接保存下元素的键值以及哈希码，并将此时元素在entries数组中的索引赋值给buckets[2]，如下图：
    2. 插入元素[33, “elem2”]，其哈希地址为：，插入后存储结构如下：
    3. 插入元素[40, “elem3”]，计算后的哈希地址为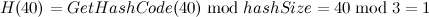，刚好未发生冲突，由于不受填装因子（此时填装因子为1）的约束，此时无须扩容，插入该元素后的存储结构为：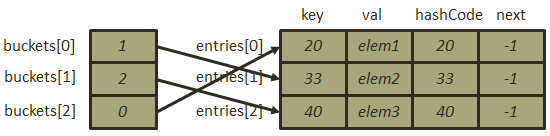
    4. 插入元素[55, “elem4”]，此时Dictionary的容量已满，必须进行扩容操作，Dictionary的扩容和Hashtable的扩容策略一致，扩容后的Dictionary的容量大小为原Dictionary容量大小2倍后的质数即也为7，然后根据扩容后的Dictionary重新寻址，这意味着部分数据可能会引起冲突从而导致已有的链表会被打乱重新组织；Dictionary首先会将扩容前Dictionary中的entries中的元素全部复制到新的entries中，紧接着进行重新寻址，对于第一个元素[20, “elem1”]，新的哈希地址为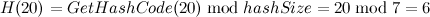：，于是buckets[6]的值被修改为0（即元素[20, “elem1”]在entries中的索引），同理对于33：，所以，buckets[5]=1，最后处理40，，此时发生冲突，在通过链表法处理冲突时，Dictionary首先将新元素的next指向冲突位置的元素索引buckets[5]，然后再将buckets[5]指向新的元素，此时一条只有两个元素的基于数组的链表形成，因此扩容之后的存储结构如下图：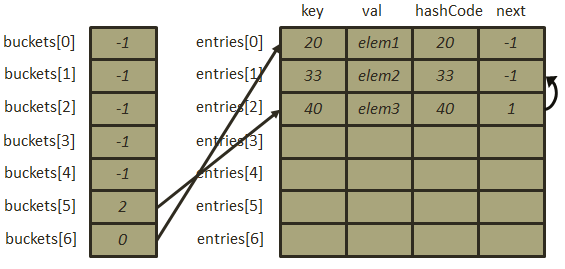

      在这里可以看出无论是Dictionary还是Hashtable，扩容带来的性能损耗代价都是相当昂贵的，因此我们最好能够预估出哈希表中最后容纳元素的总数，在哈希表初始化时就对其进行内存分配，从而避免不必要的扩容带来的性能损耗；
      此时再插入元素[55, “elem4”]，计算其哈希地址：，再次发生冲突，那么按照刚刚的冲突解决办法，插入该元素之后的存储结构为：
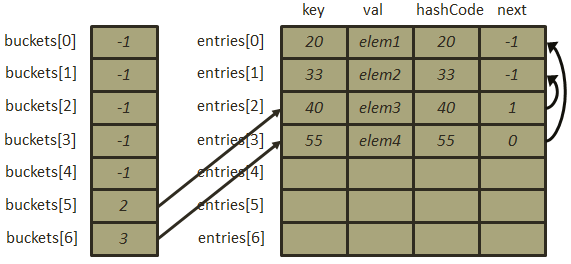
    5. 最后插入元素[13, “elem5”]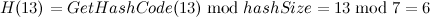，，再次冲突发生，那么插入该元素之后的结构图如下：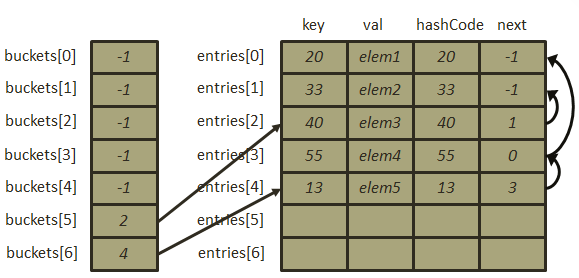
    6. 删除元素对于Dictionary来说就很简单了，如果在非冲突链上删除元素，非常简单，通过哈希算法寻址找到对应的元素删除并将buckets中对应的元素值修改为-1，如果在冲突链上删除元素，那么就是一个简单的删除链表元素的操作，在这里就留给读者去思考。

    参考资料

    作者：LukyW
    本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利.

    平衡二叉树思想及C语言实现 - - ITeye技术网站 - Google Chrome (2013/9/7 15:06:02)

    平衡二叉树思想及C语言实现

    博客分类： 
    CC++C#D语言算法 

    [转]http://blogold.chinaunix.net/u3/105029/showart_2320608.html

     

    形态匀称的二叉树称为平衡二叉树 (Balanced binary tree) ，其严格定义是：
    　　一棵空树是平衡二叉树；若 T 是一棵非空二叉树，其左、右子树为 TL 和 TR ，令 hl 和 hr 分别为左、右子树的深度。当且仅当
    　　　①TL 、 TR 都是平衡二叉树； 
    　　　② ｜ hl － hr ｜≤ 1；
    时，则 T 是平衡二叉树。
    【例】如图 8.3 所示。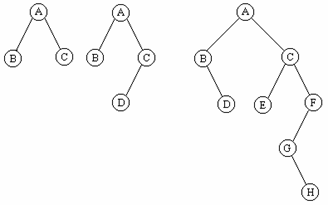

    （a）平衡二叉树           （b）非平衡二叉树
                          图8.3 平衡二叉树与非平衡二叉树
    相应地定义 hl － hr 为二叉平衡树的平衡因子 (balance factor) 。因此，平衡二叉树上所有结点的平衡因子可能是 -1 ， 0 ， 1 。换言之，若一棵二叉树上任一结点的平衡因子的绝对值都不大于 1 ，则该树是就平衡二叉树。
    动态平衡技术 
    1.动态平衡技术
    Adelson-Velskii 和 Landis 提出了一个动态地保持二叉排序树平衡的方法，其基本思想是：
    　　在构造二叉排序树的过程中，每当插入一个结点时，首先检查是否因插入而破坏了树的平衡性，如果是因插入结点而破坏了树的平衡性，则找出其中最小不平衡子树，在保持排序树特性的前提下，调整最小不平衡子树中各结点之间的连接关系，以达到新的平衡。通常将这样得到的平衡二叉排序树简称为 AVL 树。
    2.最小不平衡子树
    　　以离插入结点最近、且平衡因子绝对值大于 1 的结点作根结点的子树。为了简化讨论，不妨假设二叉排序树的最小不平衡子树的根结点为 A ，则调整该子树的规律可归纳为下列四种情况：
    （1） LL 型：
    　　新结点 X 插在 A 的左孩子的左子树里。调整方法见图 8.5(a) 。图中以 B 为轴心，将 A 结点从 B 的右上方转到 B 的右下侧，使 A 成为 B 的右孩子。


      图8.5 平衡调整的4种基本类型（结点旁的数字是平衡因子）
    （2）RR 型：
    　　新结点 X 插在 A 的右孩子的右子树里。调整方法见图 8.5(b) 。图中以 B 为轴心，将 A 结点从 B 的左上方转到 B 的左下侧，使 A 成为 B 的左孩子。
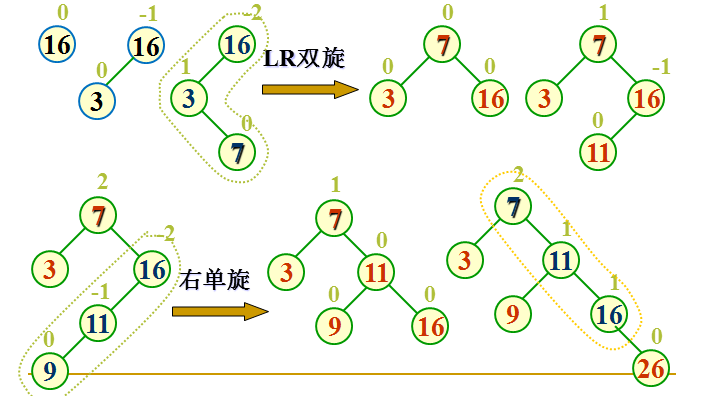
    （3）LR 型：
    　　新结点 X 插在 A 的左孩子的右子树里。调整方法见图 8.5(c) 。分为两步进行：第一步以 X 为轴心，将 B 从 X 的左上方转到 X 的左下侧，使 B 成为 X 的左孩子， X 成为 A 的左孩子。第二步跟 LL 型一样处理 ( 应以 X 为轴心 ) 。 
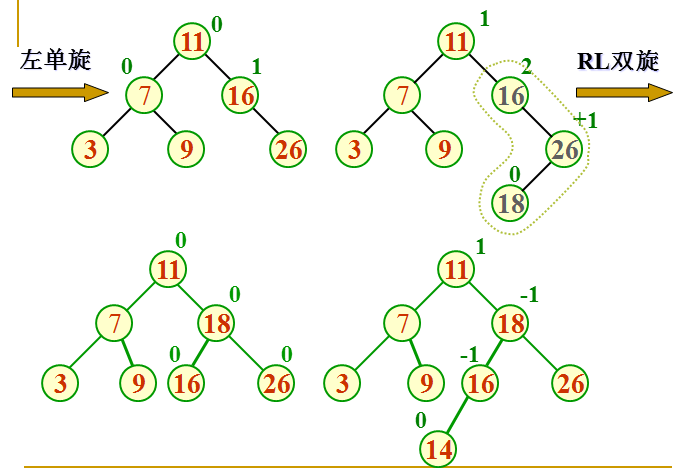
    （4）RL 型：
    　　新结点 X 插在 A 的右孩子的左子树里。调整方法见图 8.5(d) 。分为两步进行：第一步以 X 为轴心，将 B 从 X 的右上方转到 X 的右下侧，使 B 成为 X 的右孩子， X 成为 A 的右孩子。第二步跟 RR 型一样处理 ( 应以 X 为轴心 ) 。
    【例】
    实际的插入情况，可能比图 8.5 要复杂。因为 A 、 B 结点可能还会有子树。现举一例说明，设一组记录的关键字按以下次序进行插入： 4 、 5 、 7 ， 2 、 1 、 3 、 6 ，其生成及调整成二叉平衡树的过程示于图 8.6 。 
    　　在图 8.6 中，当插入关键字为 3 的结点后，由于离结点 3 最近的平衡因子为 2 的祖先是根结点 5 。所以，第一次旋转应以结点 4 为轴心，把结点 2 从结点 4 的左上方转到左下侧，从而结点 5 的左孩子是结点 4 ，结点 4 的左孩子是结点 2 ，原结点 4 的左孩子变成了结点 2 的右孩子。第二步再以结点 4 为轴心，按 LL 类型进行转换。这种插入与调整平衡的方法可以编成算法和程序，这里就不再讨论了。 


     
       图 8.6 二叉平衡树插入结点 ( 结点旁的数字为其平衡因子 )

    代码实现：
    utl.h

    #ifndef UTL_H_
    #define UTL_H_
    /*
     *整理了一些常用的功能，如内存管理
     */
    #include <stdio.h>
    #include <stdlib.h>

    /*申请内存*/
    inline void *xalloc(int size)
    {
        void *p;
        p = (void *)malloc(size);
        /*申请失败*/
        if(p == NULL)
        {
            printf("alloc error ");
            exit(1);
        }
        return p;
    }
    /*内存释放*/
    #define xfree(p) free(p)

    #endif

     

    avl.h

    #ifndef AVL_H__
    #define AVL_H__
    /*
     *avl树数据结构及相关操作
     */
    #include <stdio.h>
    #include <stdlib.h>

    struct AVLTree
    {
        unsigned int nData;    /*存储数据*/
        struct AVLTree* pLeft;    /*指向左子树*/
        struct AVLTree* pRight;    /*指向右子树*/
        int nHeight;    /*树的平衡度*/
    };

    /*插入操作*/
    struct AVLTree* insert_tree(unsigned int nData, struct AVLTree* pNode);

    /*查找操作，找到返回1，否则，返回0*/
    int find_tree(unsigned int data, struct AVLTree* pRoot);

    /*删除操作,删除所有节点*/
    void delete_tree(struct AVLTree** ppRoot);

    /*打印操作*/
    void print_tree(struct AVLTree* pRoot);

    #endif

     

    avl.c

    #include "avl.h"

    #include "utl.h"

    static int Max(int a, int b);
    static int Height(struct AVLTree* pNode);

    /*旋转操作*/
    static struct AVLTree* SingleRotateWithLeft(struct AVLTree* pNode);
    static struct AVLTree* SingleRotateWithRight(struct AVLTree* pNode);
    static struct AVLTree* DoubleRotateWithLeft(struct AVLTree* pNode);
    static struct AVLTree* DoubleRotateWithRight(struct AVLTree* pNode);

    struct AVLTree* insert_tree(unsigned int nData, struct AVLTree* pNode)
    {
        if (NULL == pNode)
        {
            pNode = (struct AVLTree*)xalloc(sizeof(struct AVLTree));
            pNode->nData = nData;
            pNode->nHeight = 0;
            pNode->pLeft = pNode->pRight = NULL;
        }
        else if (nData < pNode->nData)    /*插入到左子树中*/
        {
            pNode->pLeft = insert_tree(nData, pNode->pLeft);
            if (Height(pNode->pLeft) - Height(pNode->pRight) == 2)    /*AVL树不平衡*/
            {
                if (nData < pNode->pLeft->nData)
                {
                    /*插入到了左子树左边, 做单旋转*/
                    pNode = SingleRotateWithLeft(pNode);
                }
                else
                {
                    /*插入到了左子树右边, 做双旋转*/
                    pNode = DoubleRotateWithLeft(pNode);
                }
            }
        }
        else if (nData > pNode->nData)    /*插入到右子树中*/
        {
            pNode->pRight = insert_tree(nData, pNode->pRight);
            if (Height(pNode->pRight) - Height(pNode->pLeft) == 2)    /*AVL树不平衡*/
            {
                if (nData > pNode->pRight->nData)
                {
                    /*插入到了右子树右边, 做单旋转*/
                    pNode = SingleRotateWithRight(pNode);
                }
                else
                {
                    /*插入到了右子树左边, 做双旋转*/
                    pNode = DoubleRotateWithRight(pNode);
                }
            }
        }

        pNode->nHeight = Max(Height(pNode->pLeft), Height(pNode->pRight)) + 1;

        return pNode;
    }


    /*删除树*/
    void delete_tree(struct AVLTree** ppRoot)
    {
        if (NULL == ppRoot || NULL == *ppRoot)
            return;

        delete_tree(&((*ppRoot)->pLeft));
        delete_tree(&((*ppRoot)->pRight));
        xfree(*ppRoot);
        *ppRoot = NULL;
    }

    /*中序遍历打印树的所有结点, 因为左结点 < 父结点 < 右结点, 因此打印出来数据的大小是递增的*/
    void print_tree(struct AVLTree* pRoot)
    {
        if (NULL == pRoot)
            return;

        static int n = 0;


        print_tree(pRoot->pLeft);
        printf("[%d]nData = %u ", ++n, pRoot->nData);
        print_tree(pRoot->pRight);
    }

    /*
     *查找操作，找到返回1，否则，返回0
     *data是待查找的数据
     *pRoot:avl树的指针
     */
    int find_tree(unsigned int data, struct AVLTree* pRoot)
    {
        static int k=1;    /*查找次数*/
        if (NULL == pRoot)
        {
            printf("not find %d times ", k);
            return 0;
        }

        if(data == pRoot->nData)
        {
            printf("find:%d times ", k);
            return 1;
        }
        else if(data < pRoot->nData)
        {
            ++k;
            return find_tree(data, pRoot->pLeft);
        }
        else if(data > pRoot->nData)
        {
            ++k;
            return find_tree(data, pRoot->pRight);
        }
    }

    static int Max(int a, int b)
    {
        return (a > b ? a : b);
    }

    /*返回节点的平衡度*/
    static int Height(struct AVLTree* pNode)
    {
        if (NULL == pNode)
            return -1;

        return pNode->nHeight;
    }

    /********************************************************************
          pNode pNode->pLeft
          /
      pNode->pLeft ==> pNode
               /
      pNode->pLeft->pRight pNode->pLeft->pRight
     *********************************************************************/
    static struct AVLTree* SingleRotateWithLeft(struct AVLTree* pNode)
    {
        struct AVLTree* pNode1;

        pNode1 = pNode->pLeft;
        pNode->pLeft = pNode1->pRight;
        pNode1->pRight = pNode;

        /*结点的位置变了, 要更新结点的高度值*/
        pNode->nHeight = Max(Height(pNode->pLeft), Height(pNode->pRight)) + 1;
        pNode1->nHeight = Max(Height(pNode1->pLeft), pNode->nHeight) + 1;

        return pNode1;
    }

    /********************************************************************
      pNode pNode->pRight
       /
      pNode->pRight ==> pNode
      /
      pNode->pRight->pLeft pNode->pRight->pLeft
     *********************************************************************/
    static struct AVLTree* SingleRotateWithRight(struct AVLTree* pNode)
    {
        struct AVLTree* pNode1;

        pNode1 = pNode->pRight;
        pNode->pRight = pNode1->pLeft;
        pNode1->pLeft = pNode;

        /*结点的位置变了, 要更新结点的高度值*/
        pNode->nHeight = Max(Height(pNode->pLeft), Height(pNode->pRight)) + 1;
        pNode1->nHeight = Max(Height(pNode1->pRight), pNode->nHeight) + 1;

        return pNode1;
    }

    static struct AVLTree* DoubleRotateWithLeft(struct AVLTree* pNode)
    {
        pNode->pLeft = SingleRotateWithRight(pNode->pLeft);

        return SingleRotateWithLeft(pNode);
    }

    static struct AVLTree* DoubleRotateWithRight(struct AVLTree* pNode)
    {
        pNode->pRight = SingleRotateWithLeft(pNode->pRight);

        return SingleRotateWithRight(pNode);
    }


    测试：

    #include <stdio.h>

    #include <time.h>

    #include "avl.h"

    int main()
    {
        int i,j;
        AVLTree* pRoot = NULL;

        srand((unsigned int)time(NULL));
        
        for (i = 0; i < 10; ++i)
        {
                j = rand();
                printf("%d ", j);
            pRoot = Insert(j, pRoot);
        }

        PrintTree(pRoot);

        DeleteTree(&pRoot);

        return 0;
    }


      平衡二叉树（AVL树）的基本操作（附有示意图） - Kay's space - 博客频道 - CSDN.NET - Google Chrome (2013/9/7 14:55:23)

       

      平衡二叉树（AVL树）的基本操作（附有示意图）

      分类： Data Structure2011-08-10 19:30 5927人阅读 评论(14) 收藏 举报
      insertdeletetreesearchclass测试

      平衡二叉树关于树的深度是平衡的，具有较高的检索效率。平衡二叉树或是一棵空树，或是具有下列性质的二叉排序树：其左子树和右子树都是平衡二叉树，而且左右子树深度之差绝对值不超过1. 由此引出了平衡因子（balance factor）的概念，bf定义为该结点的左子树的深度减去右子树的深度（有些书是右子树深度减去左子树深度，我是按照左子树减去右子树来计算的，下面的代码也是这样定义的），所以平衡二叉树的结点的平衡因子只可能是 -1，0，1 ，某个结点的平衡因子绝对值大于1，该二叉树就不平衡。

      平衡二叉树在出现不平衡状态的时候，要进行平衡旋转处理，有四种平衡旋转处理（单向右旋处理，单向左旋处理，双向旋转（先左后右）处理，双向旋转（先右后左）处理），归根到底是两种（单向左旋处理和单向右旋处理）。

      文件"tree.h"

       

      1. #include<iostream>  
      2. #include<stack>  
      3. #include<queue>  
      4. using namespace std;  
      5.   
      6. const int LH=1; //左子树比右子树高1  
      7. const int EH=0; //左右子树一样高  
      8. const int RH=-1;//右子树比左子树高1  
      9. const int MAX_NODE_NUM=20; //结点数目上限  
      10.   
      11. class AVL_Tree;  
      12.   
      13. class AvlNode  
      14. {  
      15.     int data;  
      16.     int bf; //平衡因子  
      17.     AvlNode *lchild;  
      18.     AvlNode *rchild;  
      19.     friend class AVL_Tree;  
      20. };  
      21.   
      22. class AVL_Tree  
      23. {  
      24. public:  
      25.     int Get_data(AvlNode *p)  
      26.     {  
      27.         return p->data;  
      28.     }  
      29.       
      30.     void Create_AVl(AvlNode *&T) //建树  
      31.     {  
      32.         cout<<"输入平衡二叉树的元素,输入-1代表结束输入：";  
      33.         int num[MAX_NODE_NUM];  
      34.         int a,i=0;  
      35.         while(cin>>a && a!=-1)  
      36.         {  
      37.             num[i]=a;  
      38.             i++;  
      39.         }  
      40.           
      41.         if(num[0]==-1)  
      42.         {  
      43.             cout<<"平衡树为空"<<endl;  
      44.             T=NULL;  
      45.             return;  
      46.         }  
      47.   
      48.         int k=i;  
      49.         bool taller=false;  
      50.         for(i=0;i<k;i++)  
      51.             Insert_Avl(T,num[i],taller);//逐个进行插入，插入过程看下面的示意图  
      52.         cout<<"_____建树完成____"<<endl;  
      53.     }  
      54.   
      55.     void L_Rotate(AvlNode *&p)   
      56.     {  
      57.         //以p为根节点的二叉排序树进行单向左旋处理  
      58.         AvlNode *rc=p->rchild;  
      59.         p->rchild=rc->lchild;  
      60.         rc->lchild=p;  
      61.         p=rc;  
      62.     }  
      63.   
      64.     void R_Rotate(AvlNode *&p)  
      65.     {  
      66.         //以p为根节点的二叉排序树进行单向右旋处理  
      67.         AvlNode *lc=p->lchild;  
      68.         p->lchild=lc->rchild;  
      69.         lc->rchild=p;  
      70.         p=lc;  
      71.     }  
      72.   
      73.     void Left_Balance(AvlNode *&T)  
      74.     {  
      75.         //以T为根节点的二叉排序树进行左平衡旋转处理  
      76.         AvlNode *lc,*rd;  
      77.         lc=T->lchild;  
      78.         switch(lc->bf)  
      79.         {  
      80.         case LH:  
      81.             //新结点插在T的左孩子的左子树上，做单向右旋处理  
      82.             T->bf=lc->bf=EH;  
      83.             R_Rotate(T);  
      84.             break;  
      85.         case RH:  
      86.             //新结点插在T的左孩子的右子树上，要进行双旋平衡处理（先左后右）  
      87.             rd=lc->rchild;  
      88.             switch(rd->bf)  
      89.             {  
      90.             case LH:  
      91.                 //插在右子树的左孩子上  
      92.                 T->bf=RH;  
      93.                 lc->bf=EH;  
      94.                 break;  
      95.             case EH:  
      96.                 T->bf=lc->bf=EH;  
      97.                 break;  
      98.             case RH:  
      99.                 T->bf=EH;  
      100.                 lc->bf=LH;  
      101.                 break;  
      102.             }  
      103.             rd->bf=EH;  
      104.             L_Rotate(T->lchild);//先对T的左子树进行单向左旋处理  
      105.             R_Rotate(T);        //再对T进行单向右旋处理  
      106.         }  
      107.     }  
      108.   
      109.     void Right_Balance(AvlNode *&T)  
      110.     {  
      111.         //以T为根节点的二叉排序树进行右平衡旋转处理  
      112.         AvlNode *rc,*ld;  
      113.         rc=T->rchild;  
      114.         switch(rc->bf)  
      115.         {  
      116.         case RH:  
      117.             //新结点插在右孩子的右子树上，进行单向左旋处理  
      118.             T->bf=rc->bf=EH;  
      119.             L_Rotate(T);  
      120.             break;  
      121.         case LH:  
      122.             //新结点插在T的右孩子的左子树上，要进行右平衡旋转处理（先右再左）  
      123.             ld=rc->lchild;  
      124.             switch(ld->bf)  
      125.             {  
      126.             case LH:  
      127.                 T->bf=LH;  
      128.                 rc->bf=EH;  
      129.                 break;  
      130.             case EH:  
      131.                 T->bf=rc->bf=EH;  
      132.                 break;  
      133.             case RH:  
      134.                 T->bf=EH;  
      135.                 rc->bf=RH;  
      136.                 break;  
      137.             }  
      138.             ld->bf=EH;  
      139.             R_Rotate(T->rchild);//先对T的右子树进行单向右旋处理  
      140.             L_Rotate(T);        //再对T进行单向左旋处理  
      141.         }  
      142.     }  
      143.   
      144.     bool Insert_Avl(AvlNode *&T,int num,bool &taller) //插入  
      145.     {  
      146.         //若在平衡二叉树中不存在结点值和num一样大小的结点  
      147.         //则插入值为num的新结点，并返回true  
      148.         //若因为插入而使得二叉排序树失去平衡，则做平衡旋转处理  
      149.         //taller反映树是否长高  
      150.           
      151.         if(!T)  
      152.         {  
      153.             //插入新结点，树长高，taller为true  
      154.             T=new AvlNode;  
      155.             T->data=num;  
      156.             T->lchild=T->rchild=NULL;  
      157.             T->bf=EH;  
      158.             taller=true;  
      159.         }  
      160.         else  
      161.         {  
      162.             if(num==T->data)  
      163.             {  
      164.                 //不重复插入  
      165.                 taller=false;  
      166.                 return false;  
      167.             }  
      168.             if(num<T->data) //继续在T的左子树中进行搜索  
      169.             {  
      170.                 if(!Insert_Avl(T->lchild,num,taller))//插入不成功  
      171.                     return false;   
      172.                 if(taller) //已插入T的左子树,且左子树长高  
      173.                 {  
      174.                     switch(T->bf)  
      175.                     {  
      176.                     case LH:  
      177.                         /*————————————————————— 
      178.                         / 插入前左子树高于右子树，需要进行做平衡处理 
      179.                         / 不管是单向左旋处理，还是先左后右平衡处理 
      180.                         / 处理结果都是使得插入新结点后，树的高度不变 
      181.                         /—————————————————————*/  
      182.                           
      183.                         Left_Balance(T);  
      184.                         taller=false;  
      185.                         break;  
      186.                     case EH:  
      187.                         //插入前左右子树等高，现在插入新街点后，左子树比右子树高  
      188.                           
      189.                         T->bf=LH;  
      190.                         taller=true;  
      191.                         break;  
      192.                     case RH:  
      193.                         //插入前右子树比左子树高，现在新结点插入左子树后，树变为左右子树等高  
      194.                           
      195.                         T->bf=EH;  
      196.                         taller=false;  
      197.                         break;  
      198.                       
      199.                     }  
      200.                 }  
      201.             }  
      202.             else  
      203.             {  
      204.                 //num>T->data 在T的右子树中继续搜索  
      205.                 if(!Insert_Avl(T->rchild,num,taller))  
      206.                     return false;  
      207.                 if(taller)  
      208.                 {  
      209.                     switch(T->bf)  
      210.                     {  
      211.                     case LH:  
      212.                         //插入前左子树比右子树高，现在插入T的右子树后，左右子树等高  
      213.                           
      214.                         T->bf=EH;  
      215.                         taller=false;  
      216.                         break;  
      217.                     case EH:  
      218.                         //插入前左右子树等高，现在插入后，右子树比左子树高  
      219.   
      220.                         T->bf=RH;  
      221.                         taller=true;  
      222.                         break;  
      223.   
      224.                     case RH:  
      225.                         //插入前右子树比坐子树高，插入后，排序树失去平衡，需要进行右平衡处理  
      226.                         Right_Balance(T);  
      227.                         taller=false;  
      228.                         break;  
      229.   
      230.                     }  
      231.                 }  
      232.             }  
      233.         }  
      234.         return true;  
      235.     }  
      236.   
      237.     bool Search_Avl(AvlNode *T,int num,AvlNode *&f,AvlNode *&p) //搜索  
      238.     {  
      239.         //用p带回查找到的顶点的地址,f带回p的双亲结点  
      240.         p=T;  
      241.         while(p)  
      242.         {  
      243.             if(p->data==num)  
      244.                 return true;  
      245.             if(p->data>num)  
      246.             {  
      247.                 f=p;  
      248.                 p=p->lchild;  
      249.             }  
      250.             else  
      251.             {  
      252.                 f=p;  
      253.                 p=p->rchild;  
      254.             }  
      255.         }  
      256.         return false;  
      257.     }  
      258.       
      1.     void Delete_AVL(AvlNode *&T,int num) //删除，删除后没有回溯到根节点，算法有错，待日后修改完善，有心的朋友可以自己加一个栈或者其他方式来实现  
      2.     {  
      3.         /*--------------------------------------------------------- 
      4.         / 从树中删除一个节点后，要保证删后的树还是一棵平衡二叉树，  
      5.         / 删除前，首先是在树中查找是否有这个结点，用p指向该结点，   
      6.         / 用f指向p的双亲结点，这个结点在树中的位置有下面四种情况:   
      7.         /                                                           
      8.         / 1:如果p指向的结点是叶子结点，那么直接将f指针的左子树或者  
      9.         / 右子树置空，然后删除p结点即可。                           
      10.         /                                                           
      11.         / 2:如果p指向的结点是只有左子树或右子树，那么只需要让p结点 
      12.         / 原来在f中的位置(左子树或右子树)用p的子树代替即可。 
      13.         / 代替后，要修改f的平衡因子，在失去平衡的时候，要调用相应的 
      14.         / 做平衡旋转或右平衡旋转进行恢复. 
      15.         /                                                           
      16.         / 3:如果p所指向的结点是根节点，那么直接将根节点置空         
      17.         /                                                           
      18.         / 4:如果p所指向的结点左右子树都非空，为了删除p后原序列的顺  
      19.         / 序不变，就需要在原序列中先找出p的直接前驱(或者直接后继)   
      20.         / 结点用那个结点的值来代替p结点的值，然后再删掉那个直接前   
      21.         / 驱(或者直接后继)结点。  
      22.         / 其中s指向的是要删除的结点，也就是p的直接前驱，q指向的是 
      23.         / s的双亲结点，此时，应该看s的平衡因子，在会出现失去平衡的 
      24.         / 情况时，就要根据实际情况采用左平衡旋转或是右平衡旋转，让 
      25.         / 树恢复平衡，这点和插入操作时是相对应的。 
      26.         /  
      27.         / 在中序遍历序列中找结点的直接前驱的方法是顺着结点的左孩子  
      28.         / 的右链域开始，一直到结点右孩子为空为止。  
      29.         /---------------------------------------------------------*/  
      30.   
      31.         AvlNode *f=NULL;  
      32.         AvlNode *p=NULL;  
      33.         AvlNode *q=NULL;  
      34.         AvlNode *s=NULL;  
      35.         if(Search_Avl(T,num,f,p))  
      36.         {  
      37.             if(p->lchild && p->rchild) //左右子树均存在时  
      38.             {  
      39.                 q=p;  
      40.                 s=p->lchild;  
      41.                 while(s->rchild)  
      42.                 {  
      43.                     q=s;  
      44.                     s=s->rchild;  
      45.                 }  
      46.                 p->data=s->data;  
      47.                 if(q!=p)  
      48.                 {  
      49.                     //q结点的右子树高度减少1  
      50.                     //所以平衡因子会+1  
      51.                     q->rchild=s->lchild;  
      52.                     switch(q->bf)  
      53.                     {  
      54.                     //删除前右子树高，现在就变成一样高  
      55.                     case RH:  
      56.                         q->bf=EH; break;  
      57.                     //删除前等高，现在就变成左子树比右子树高  
      58.                     case EH:  
      59.                         q->bf=LH; break;  
      60.                     //删除前左子树高，现在左子树又高了一，所以失去平衡  
      61.                     case LH:  
      62.                         q->bf=EH;  
      63.                         Left_Balance(q);  
      64.                         break;  
      65.                     }  
      66.                 }  
      67.                 else  
      68.                 {  
      69.                     //p的左子树的右子树为空时  
      70.                     //q结点也就是p结点，由于s的右子树为空  
      71.                     //所以q结点的左子树高度降低1  
      72.                     //平衡因子-1  
      73.                     q->lchild=s->lchild;  
      74.                     switch(q->bf)  
      75.                     {  
      76.                     case LH:  
      77.                         q->bf=EH;break;  
      78.                     case EH:  
      79.                         q->bf=RH;break;  
      80.                     case RH:  
      81.                         q->bf=EH;  
      82.                         Right_Balance(q);  
      83.                         break;  
      84.                     }  
      85.                 }  
      86.                 delete s;  
      87.                 cout<<"删除结点成功"<<endl;  
      88.                 return ;  
      89.             }  
      90.             else  
      91.             {  
      92.                 if(!p->lchild)  
      93.                 {  
      94.                     q=p;  
      95.                     p=p->rchild;  
      96.                 }  
      97.                 else  
      98.                 {  
      99.                     q=p;  
      100.                     p=p->lchild;  
      101.                 }  
      102.                 if(!T)  
      103.                 {  
      104.                     T->bf=EH;  
      105.                     T=p;  
      106.                 }  
      107.                 else if(q==f->lchild)  
      108.                 {  
      109.                     f->lchild=p;  
      110.                     switch(f->bf)  
      111.                     {  
      112.                     case LH:  
      113.                         f->bf=EH; break;  
      114.                     case EH:  
      115.                         f->bf=RH; break;  
      116.                     case RH:  
      117.                         f->bf=EH;  
      118.                         Right_Balance(f);  
      119.                         break;  
      120.                     }  
      121.                 }  
      122.                 else  
      123.                 {  
      124.                     f->rchild=p;  
      125.                     switch(f->bf)  
      126.                     {  
      127.                     case RH:  
      128.                         f->bf=EH; break;  
      129.                     case EH:  
      130.                         f->bf=LH; break;  
      131.                     case LH:  
      132.                         f->bf=EH;  
      133.                         Left_Balance(f);  
      134.                         break;  
      135.                     }  
      136.                 }  
      137.                 delete q;  
      138.                 cout<<"删除结点成功"<<endl;  
      139.                 return;  
      140.             }  
      141.         }  
      142.         else  
      143.         {  
      144.             cout<<"要删除的结点不存在"<<endl;  
      145.             return;  
      146.         }  
      147.     }  
      148.   
      149.     InOrder_Traverse(AvlNode *T) //中序遍历  
      150.     {  
      151.         stack<AvlNode *> s;  
      152.         AvlNode *p=T;  
      153.   
      154.         while(p || !s.empty())  
      155.         {  
      156.             if(p)  
      157.             {  
      158.                 s.push(p);  
      159.                 p=p->lchild;  
      160.             }  
      161.             else  
      162.             {  
      163.                 p=s.top();  
      164.                 s.pop();  
      165.                 cout<<p->data<<"  ";  
      166.                 p=p->rchild;  
      167.             }  
      168.         }  
      169.     }  
      170.   
      171.     void Level_Traverse(AvlNode *T) //层次遍历  
      172.     {  
      173.         queue<AvlNode *> q;  
      174.         AvlNode *p=T;  
      175.         q.push(p);  
      176.         while(!q.empty())  
      177.         {  
      178.             p=q.front();  
      179.             q.pop();  
      180.             cout<<p->data<<"  ";  
      181.             if(p->lchild)  
      182.                 q.push(p->lchild);  
      183.             if(p->rchild)  
      184.                 q.push(p->rchild);  
      185.         }  
      186.     }  
      187.   
      188. };  
      测试文件"main.cpp"

       

       

      1. #include"tree.h"  
      2.   
      3. int main()  
      4. {  
      5.     AVL_Tree tree;  
      6.     AvlNode *root=NULL;  
      7.     cout<<"____建立平衡二叉树____"<<endl;  
      8.     tree.Create_AVl(root);  
      9.   
      10.     cout<<"中序遍历二叉树为：";  
      11.     tree.InOrder_Traverse(root);  
      12.     cout<<endl;  
      13.       
      14.     cout<<"层次遍历二叉树为：";  
      15.     tree.Level_Traverse(root);  
      16.     cout<<endl;  
      17.   
      18.     int num;  
      19.     bool taller=false;  
      20.     cout<<"输入你要插入的结点的值：";  
      21.     cin>>num;  
      22.     tree.Insert_Avl(root,num,taller);  
      23.   
      24.     cout<<"中序遍历二叉树为：";  
      25.     tree.InOrder_Traverse(root);  
      26.     cout<<endl;  
      27.   
      28.     AvlNode *f=NULL;  
      29.     AvlNode *p=NULL;  
      30.     cout<<"输入你要搜索的结点的值：";  
      31.     cin>>num;  
      32.     if(tree.Search_Avl(root,num,f,p))  
      33.     {  
      34.         cout<<"查找得到的结点值为："<<tree.Get_data(p)<<"的地址为："<<p<<endl;  
      35.         if(f==NULL)  
      36.             cout<<"因为结点"<<tree.Get_data(p)<<"是根结点，所以没有双亲结点"<<endl;  
      37.         else  
      38.             cout<<"该结点的双亲结点的值为："<<tree.Get_data(f)<<endl;  
      39.     }  
      40.     else  
      41.         cout<<"查找的结点不存在"<<endl;  
      42.   
      43.     cout<<"输入你要删除的结点的值：";  
      44.     cin>>num;  
      45.     tree.Delete_AVL(root,num);  
      46.   
      47.     cout<<"中序遍历二叉树为：";  
      48.     tree.InOrder_Traverse(root);  
      49.     cout<<endl;  
      50.   
      51.     return 0;  
      52. }  

       

      测试结果

       

      1. ____建立平衡二叉树____  
      2. 输入平衡二叉树的元素,输入-1代表结束输入：16 3 7 11 9 26 18 14 15 -1  
      3. _____建树完成____  
      4. 中序遍历二叉树为：3  7  9  11  14  15  16  18  26  
      5. 层次遍历二叉树为：11  7  18  3  9  15  26  14  16  
      6. 输入你要插入的结点的值：20  
      7. 中序遍历二叉树为：3  7  9  11  14  15  16  18  20  26  
      8. 输入你要搜索的结点的值：20  
      9. 查找得到的结点值为：20的地址为：00380BB0  
      10. 该结点的双亲结点的值为：26  
      11. 输入你要删除的结点的值：15  
      12. 删除结点成功  
      13. 中序遍历二叉树为：3  7  9  11  14  16  18  20  26  
      14. Press any key to continue  

       

      下面是四种旋转的示意图

      先右后左的和先左后右的相对应的 所以不画了 下面再画一个建树的过程 就不画了 太费时间了画这个 刚好找到一个画好的 直接贴 

      因为下面图中它的计算平衡因子的方式是右子树高度减去左子树高度，所以和我上面的计算方法相反，不过不影响观看

      建立含有元素 16 3 7 11 9 26 18 14 15  的平衡二叉树的过程如下所示：

       

        二叉排序树（二叉搜索树） - Kay's space - 博客频道 - CSDN.NET - Google Chrome (2013/9/7 14:54:19)

        二叉排序树（二叉搜索树）

        分类： Data Structure2011-08-07 11:47 920人阅读 评论(1) 收藏 举报
        insertsearchclasstreedelete数据结构

        动态查找表的一种理想数据结构。

        二叉排序树的定义是：二叉排序树T是一棵树,它或者是空，或者具备一下三条性质：

        （1）、如果T的根节点的左子树非空，其左子树所有结点的值均小于T的根节点的值

        （2）、如果T的根节点的右子树非空，其右子树所有结点的值均大于T的根节点的值
        （3）、T的根结点的左右子树均为二叉排序树

        下面是代码：

        文件"tree.h"

        1. #include<iostream>  
        2. #include<stack>  
        3. #include<queue>  
        4. using namespace std;  
        5.   
        6. #define MAX_NODE_NUM 20 //树结点最大值  
        7. class Bin_Sort_Tree;  
        8. //树结点  
        9. class BSTnode  
        10. {  
        11.     int tag;//后序遍历作为访问标志  
        12.     int data;  
        13.     BSTnode *lchild;  
        14.     BSTnode *rchild;  
        15.     friend class Bin_Sort_Tree;  
        16. };  
        17.   
        18. //二叉排序树  
        19. class Bin_Sort_Tree  
        20. {  
        21. public:   
        22.     int Get_data(BSTnode *p)  
        23.     {  
        24.         return p->data;  
        25.     }  
        26.   
        27.     bool Search_BST(BSTnode *T,int a,BSTnode *&f,BSTnode *&p)  
        28.     {  
        29.         /*----------------------------- 
        30.         /在树中查找值为a的结点，查找到  
        31.         /了，用p保存该结点地址，f指向  
        32.         /p的双亲结点                    
        33.         /-----------------------------*/  
        34.         p=T;  
        35.         while(p)  
        36.         {  
        37.             if(p->data==a)  
        38.                 return true;  
        39.             else if(p->data>a)  
        40.             {  
        41.                 f=p;  
        42.                 p=p->lchild;  
        43.             }  
        44.             else  
        45.             {  
        46.                 f=p;  
        47.                 p=p->rchild;  
        48.             }  
        49.         }  
        50.         return false;  
        51.     }  
        52.       
        53.     //将值为a的结点插入树中，若值已存在，就不插入  
        54.     void Insert_BST_1(BSTnode *&T,int a)  
        55.     {  
        56.         BSTnode *f=NULL;  
        57.         BSTnode *p=NULL;  
        58.         if(Search_BST(T,a,f,p))  
        59.             return; //树中已有值相同结点，不插入  
        60.         else  
        61.         {  
        62.             BSTnode *s=new BSTnode;  
        63.             s->data=a;  
        64.             s->lchild=s->rchild=NULL;  
        65.             if(s->data>f->data)  
        66.                 f->rchild=s;  
        67.             else  
        68.                 f->lchild=s;  
        69.         }  
        70.     }  
        71.       
        72.     void Insert_BST_2(BSTnode *&T,int a) //插入算法递归实现  
        73.     {     
        74.         if(!T)  
        75.         {  
        76.             cout<<"树为空"<<endl;  
        77.             return;  
        78.         }  
        79.         if(T->data>a)  
        80.         {  
        81.             if(!T->lchild)  
        82.             {  
        83.                 T->lchild=new BSTnode;  
        84.                 T->lchild->data=a;  
        85.                 T->lchild->lchild=NULL;  
        86.                 T->lchild->rchild=NULL;  
        87.                 return;  
        88.             }  
        89.             else  
        90.                 Insert_BST_2(T->lchild,a);  
        91.         }  
        92.         if(T->data<a)  
        93.         {  
        94.             if(!T->rchild)  
        95.             {  
        96.                 T->rchild=new BSTnode;  
        97.                 T->rchild->data=a;  
        98.                 T->rchild->lchild=NULL;  
        99.                 T->rchild->rchild=NULL;  
        100.                 return;  
        101.             }  
        102.             else  
        103.                 Insert_BST_2(T->rchild,a);  
        104.         }  
        105.   
        106.     }  
        107.   
        108.     void Create_BSTree(BSTnode *&T) //建树  
        109.     {  
        110.         cout<<"输入二叉排序树的元素,输入-1代表结束输入：";  
        111.         int num[MAX_NODE_NUM];  
        112.         int a,i=0;  
        113.         while(cin>>a && a!=-1)  
        114.         {  
        115.             num[i]=a;  
        116.             i++;  
        117.         }  
        118.           
        119.         if(num[0]==-1)  
        120.         {  
        121.             cout<<"排序树为空"<<endl;  
        122.             return;  
        123.         }  
        124.   
        125.         int k=i;  
        126.         T=new BSTnode;  
        127.         T->data=num[0];  
        128.         T->lchild=T->rchild=NULL;  
        129.         for(i=1;i<k;i++)  
        130.             Insert_BST_1(T,num[i]);  
        131.         cout<<"____建树完成____"<<endl;  
        132.     }  
        133.   
        134.     void Delete_BST(BSTnode *&T,int a)//删除结点值为a的结点  
        135.     {  
        136.         /*--------------------------------------------------------- 
        137.         / 从树中删除一个节点后，要保证删后的树还是一棵二叉排序树，  
        138.         / 删除前，首先是在树中查找是否有这个结点，用p指向该结点，   
        139.         / 用f指向p的双亲结点，这个结点在树中的位置有下面四种情况:   
        140.         /                                                           
        141.         / 1:如果p指向的结点是叶子结点，那么直接将f指针的左子树或者  
        142.         / 右子树置空，然后删除p结点即可。                           
        143.         /                                                           
        144.         / 2:如果p指向的结点是只有左子树或右子树，那么只需要让p结点  
        145.         / 原来在f中的位置(左子树或右子树)用p的子树代替即可。        
        146.         /                                                           
        147.         / 3:如果p所指向的结点是根节点，那么直接将根节点置空         
        148.         /                                                           
        149.         / 4:如果p所指向的结点左右子树都非空，为了删除p后原序列的顺  
        150.         / 序不变，就需要在原序列中先找出p的直接前驱(或者直接后继)   
        151.         / 结点用那个结点的值来代替p结点的值，然后再删掉那个直接前   
        152.         / 驱(或者直接后继)结点。                                    
        153.         / 在中序遍历序列中找结点的直接前驱的方法是顺着结点的左孩子  
        154.         / 的右链域开始，一直到结点右孩子为空为止。                  
        155.         /---------------------------------------------------------*/  
        156.   
        157.         BSTnode *f=NULL;  
        158.         BSTnode *p=NULL;  
        159.         BSTnode *q=NULL;  
        160.         BSTnode *s=NULL;  
        161.         if(Search_BST(T,a,f,p))  
        162.         {  
        163.             if(p->lchild && p->rchild)  
        164.             {  
        165.                 q=p;  
        166.                 s=p->lchild;  
        167.                 while(s->rchild)  
        168.                 {  
        169.                     q=s;  
        170.                     s=s->rchild;  
        171.                 }  
        172.                 p->data=s->data;  
        173.                 //s指向要删除结点的直接前驱，且s是一定没有右子树的  
        174.                 if(q!=p)  
        175.                     q->rchild=s->lchild;  
        176.                 else  
        177.                     q->lchild=s->lchild;//这种情况是,q的左子树的右子树为空时  
        178.                 delete s;  
        179.                 cout<<"结点删除成功"<<endl;  
        180.                 return ;  
        181.             }  
        182.             else   
        183.             {  
        184.                 if(!p->lchild) //左子树为空  
        185.                 {  
        186.                     q=p;  
        187.                     p=p->rchild;  
        188.                 }  
        189.                 else        //右子树为空  
        190.                 {  
        191.                     q=p;  
        192.                     p=p->lchild;  
        193.                 }  
        194.                 //下面将p所指向的子树连接到f所指(被删结点的双亲)的结点上  
        195.                 if(!T) //被删的结点为根节点  
        196.                     T=p;  
        197.                 else if(q==f->lchild)  
        198.                     f->lchild=p;  
        199.                 else  
        200.                     f->rchild=p;  
        201.                 delete q;  
        202.                 cout<<"结点删除成功"<<endl;  
        203.                 return;  
        204.             }  
        205.         }  
        206.         else  
        207.         {  
        208.             cout<<"要删除的结点不存在"<<endl;  
        209.             return ;  
        210.         }  
        211.     }  
        212.   
        213.     //下面是二叉树的四种遍历方式，都是非递归方式实现  
        214.       
        215.     void PreOrder_Traverse(BSTnode *T) //前序遍历  
        216.     {  
        217.         stack<BSTnode *> s;  
        218.         BSTnode *p;  
        219.         p=T;  
        220.         while(p || !s.empty())  
        221.         {  
        222.             if(p)  
        223.             {  
        224.                 cout<<p->data<<"  ";  
        225.                 s.push(p);  
        226.                 p=p->lchild;  
        227.             }  
        228.             else  
        229.             {  
        230.                 p=s.top();  
        231.                 s.pop();  
        232.                 p=p->rchild;  
        233.             }  
        234.         }  
        235.     }  
        236.   
        237.     void InOrder_Traverse(BSTnode *T) //中序遍历  
        238.     {  
        239.         stack<BSTnode *> s;  
        240.         BSTnode *p=T;  
        241.         while(p || !s.empty())  
        242.         {  
        243.             if(p)  
        244.             {  
        245.                 s.push(p);  
        246.                 p=p->lchild;  
        247.             }  
        248.             else  
        249.             {  
        250.                 p=s.top();  
        251.                 s.pop();  
        252.                 cout<<p->data<<"  ";  
        253.                 p=p->rchild;  
        254.             }  
        255.         }  
        256.     }  
        257.   
        258.     void PostOrder_Traverse(BSTnode *T) //后序遍历  
        259.     {  
        260.         stack<BSTnode *> s;  
        261.         BSTnode *p=T;  
        262.         while(p || !s.empty())  
        263.         {  
        264.             if(p)  
        265.             {  
        266.                 p->tag=0;  
        267.                 s.push(p);  
        268.                 p=p->lchild;  
        269.             }  
        270.             else  
        271.             {  
        272.                 p=s.top();  
        273.                 if(p->tag)  
        274.                 {  
        275.                     cout<<p->data<<"  ";  
        276.                     s.pop();  
        277.                     p=NULL;  
        278.                 }  
        279.                 else  
        280.                 {  
        281.                     p->tag=1;  
        282.                     p=p->rchild;  
        283.                 }  
        284.             }  
        285.         }  
        286.     }  
        287.   
        288.     void LevelOrder_Traverse(BSTnode *T) //层次遍历  
        289.     {  
        290.         queue<BSTnode *> q;  
        291.         BSTnode *p=T;  
        292.         q.push(p);  
        293.         while(!q.empty())  
        294.         {  
        295.             p=q.front();  
        296.             q.pop();  
        297.             cout<<p->data<<"  ";  
        298.             if(p->lchild)  
        299.                 q.push(p->lchild);  
        300.             if(p->rchild)  
        301.                 q.push(p->rchild);  
        302.         }  
        303.     }  
        304. };  

        主函数"main.cpp"

        1. #include"tree.h"  
        2.   
        3. int main()  
        4. {  
        5.     Bin_Sort_Tree tree;  
        6.     BSTnode *root=NULL;  
        7.       
        8.     cout<<"_____建立二叉排序树____"<<endl;  
        9.     tree.Create_BSTree(root);  
        10.   
        11.     cout<<"前序遍历二叉树为：";  
        12.     tree.PreOrder_Traverse(root);  
        13.     cout<<endl;  
        14.   
        15.     cout<<"中序遍历二叉树为：";  
        16.     tree.InOrder_Traverse(root);  
        17.     cout<<endl;  
        18.   
        19.     cout<<"后序遍历二叉树为：";  
        20.     tree.PostOrder_Traverse(root);  
        21.     cout<<endl;  
        22.   
        23.     cout<<"层次遍历二叉树为：";  
        24.     tree.LevelOrder_Traverse(root);  
        25.     cout<<endl;  
        26.   
        27.     int data;  
        28.     BSTnode *f=NULL;  
        29.     BSTnode *p=NULL;  
        30.     cout<<"输入你要搜索的结点的值：";  
        31.     cin>>data;  
        32.     if(tree.Search_BST(root,data,f,p))  
        33.     {  
        34.         cout<<"你所搜索的结点地址为："<<p<<endl;  
        35.         cout<<"他的双亲结点值为："<<tree.Get_data(f)<<endl;  
        36.     }  
        37.     else  
        38.         cout<<"树中没有你要找的结点"<<endl;  
        39.   
        40.     cout<<"输入你要删除的结点的值：";  
        41.     cin>>data;  
        42.     tree.Delete_BST(root,data);  
        43.     cout<<"删除后的二叉树的中序遍历为：";  
        44.     tree.InOrder_Traverse(root);  
        45.     cout<<endl;  
        46.   
        47.     cout<<"输入你要插入树中的值：";  
        48.     cin>>data;  
        49.     tree.Insert_BST_2(root,data);  
        50.     cout<<"插入后，树的中序遍历为：";  
        51.     tree.InOrder_Traverse(root);  
        52.     cout<<endl;  
        53.   
        54.     return 0;  
        55. }  

        下面是测试结果

        1. _____建立二叉排序树____  
        2. 输入二叉排序树的元素,输入-1代表结束输入：5 7 3 2 9 4 8 8 1 10 -1  
        3. ____建树完成____  
        4. 前序遍历二叉树为：5  3  2  1  4  7  9  8  10  
        5. 中序遍历二叉树为：1  2  3  4  5  7  8  9  10  
        6. 后序遍历二叉树为：1  2  4  3  8  10  9  7  5  
        7. 层次遍历二叉树为：5  3  7  2  4  9  1  8  10  
        8. 输入你要搜索的结点的值：7  
        9. 你所搜索的结点地址为：00380D18  
        10. 他的双亲结点值为：5  
        11. 输入你要删除的结点的值：10  
        12. 结点删除成功  
        13. 删除后的二叉树的中序遍历为：1  2  3  4  5  7  8  9  
        14. 输入你要插入树中的值：6  
        15. 插入后，树的中序遍历为：1  2  3  4  5  6  7  8  9  
        16. Press any key to continue  

        按照一开始建树时的输入，生成的树为：


        淘宝搜索：定向抓取网页技术漫谈 -- 算法 -- IT技术博客大学习 -- 共学习 共进步！ - Google Chrome (2013/8/9 18:15:46)

        淘宝搜索：定向抓取网页技术漫谈

           出处信息

            网络爬虫(web crawler)又称为网络蜘蛛(web spider)是一段计算机程序，它从互联网上按照一定的逻辑和算法抓取和下载互联网的网页,是搜索引擎的一个重要组成部分。一般的爬虫从一部分start url开始，按照一定的策略开始爬取，爬取到的新的url在放入到爬取队列之中，然后进行新一轮的爬取，直到抓取完毕为止。

            我们看一下crawler一般会遇到什么样的问题吧：

        • 抓取的网页量很大
        • 网页更新量也很大，一般的网站，比如新闻，电子商务网站，页面基本是实时更新的
        • 大部分的网页都是动态的，多媒体，或者封闭的(需要登录才能查看)

            海量网页的存在就意味着在一定时间之内，抓取只能的抓取其中的一部分，因此需要定义清楚抓取的优先级；网页更新的频繁，也就意味着需要抓取最新的网页和保证链接的有效性，因此一个更有可能带来新网页的列表页显得尤为重要；对于新闻网站，新的网站一般出现在首页，或者在指定的分类网页，但是对于淘宝来说，商品的更新就很难估计了；动态网页怎么办呢？现在的网页大都有JS和AJAX，抓取已经不是简单的执行wget下载，现代的网页结构需要我们的爬虫更加智能，需要更灵活的应对网页的各种情况。

            因此，对一个通用的爬虫个，我们要定义

        • 抓取策略，那些网页是我们需要去下载的，那些是无需下载的，那些网页是我们优先下载的，定义清楚之后，能节省很多无谓的爬取
        • 更新策略，监控列表页来发现新的页面；定期check页面是否过期等等
        • 抽取策略，我们应该如何的从网页中抽取我们想要的内容，不仅仅包含最终的目标内容，还有下一步要抓取的url
        • 抓取频率，我们需要合理的去下载一个网站，却又不失效率

            抓取策略

            使用URL的正则特征是一个简单但却很高效的模式；对于定向抓取，一般的网站的URL有一定的特征，比如可能仅仅关心 .html, .htm, .asp, .aspx, .php, .jsp, .jspx类型的网页；或者是如果可以得到目标网站的正则，则可以大大的降低抓取的数量；又或者我们无需关心某一类网页，比如我们不抓取bbs.taobao.com下面的内容；仅仅需要抓取淘宝的商品页面(http://item.taobao.com/item.htm?id=\d+ )。通过URL的正则能极大的降低抓取数量；

            也可以通过网页的文本特征来确定；不过要复杂得多了，一般需要一定数量已知页面的训练集合，然后提取页面的文本特征，然后通过向量空间模型或者其其他基于主题词提取的模型计算目标网页和训练集网页的距离，决定是否是目标网页。

            更新策略

            Freshness：表示抓取到的网页是否已经被修改

            

            Age：表示抓取的网页过期的时间

            

            对于更新来说，目标是让平均age时间越小，freshness越高；一般的更新策略有两种：定期批量更新和按更新周期更新；定期批量更新指对一批URL，按照失效时间定期去刷新，按周期更新指的是按照页面更新变化频率而修正是更新频率，一般来说，更新越频繁的网页更新也就越快。

            抽取策略：

            XPATH是一个简单直观，但是很有效的一个方案，XPATH能精准的定位网页的任意一个位置，意味着我们可以很精准的抽取页面上的任意位置，当面临很多网站的时候，当然配置XPATH就是一个很艰巨的任务，也许存在一个自适应的XPATH识别的方法。

            JS和AJAX

            在java下面，HtmlUnit是一个不错的解决方案，HtmlUnit是Junit 的扩展测试框架之一，该框架模拟浏览器的行为，开发者可以使用其提供的API对页面的元素进行操作，套用官方网站的话HtmlUnit“是Java程序的浏览器”。HtmlUnit支持HTTP，HTTPS，COOKIE，表单的POST和GET方法，能够对HTML文档进行包装，页面的各种元素都可以被当作对象进行调用，另外对JavaScript的支持也比较好。一般来说，HtmlUnit是在java环境下解决JS的很好的选择

            WebKit包含一个网页引擎WebCore和一个脚本引擎JavaScriptCore，它们分别对应的是KDE的KHTML和KJS；目前比较主流的浏览器Google Chrome和Apple的safari，都是基于WebKit的内核写的。使用浏览器作为抓取能更好的模拟用户浏览的行为，能够天然的解决JS和AJAX等问题，问题可能就是性能是一个瓶颈。

            抓取频率

            同时开启N个线程抓取一个网站，相信很快就会被对方网站封掉；因此抓取的频率也很重要；抓取网站同时不对对方网站造成压力；在robot.txt协议里面定义Crawl-delay来确定抓取的频率也是一种网站的通用的做法，对于一般的抓取而言，10到20秒抓取一次是一个比较保险的频率，也有提出10*t的抓取间隔(t是download时间)比较合理

            定向抓取的框架

            通用抓取架构，如下图

            

            多线程下载模块(Multi-threaded downloader)

            该模块一般包含：

        • 下载模块，下载网页，并应对一些web的一些错误，包括redirect等等
        • DNS解析模块，网页数量很多的时候，我们需要一个本地的DNS解析模块来维护domain到IP的映射
        • 链接抽取模块，抽取下一步要抓取的链接(follow link)

            调度模块(schedule)

            调度模块是抓取系统的核心，调度模块从url队列里面选择一批url喂到下载模块下载；其中会涉及到

        • url调度，调度模块按照一定的策略，选取url进入抓取系统
        • url除重，一定时期之内已经抓取的网页，不再抓取

            原始文章：http://www.searchtb.com/2011/01/an-introduction-to-crawler.html

        哈希函数详解-leon_yu-ChinaUnix博客 - Google Chrome (2013/8/7 22:54:07)

        哈希函数详解 2012-08-09 17:38:30

        分类： LINUX

         

        散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。
         
        这是来自wiki的解释，为了透彻理解这个问题，我们举个简单的例子…
         
        比如项羽要分封十八路诸侯，这十八路诸侯倒秦功劳、实力以及对项羽的忠诚度不一而足，如何分封、管制就是一个大问题。每个诸侯包括拥有兵力，封王地域等诸多信息，把这些信息全放进一个结构体，我们只要知道这个结构体地址，即可知道该王所有信息。我们声明一个有序数组king_value[n]，把每个封王(结构体指针)放在king_value []中占一项，那么项王只要拥有king_value [n]这个数组，就可以快速调用天下诸侯的所有信息。
         
        问题就出现了，假如你要查找某个诸侯的资料，必须把这个数组遍历一遍，时间复杂度是O(n),明显的n越大，找到某个封王的时间就越长，是相当低效的。
         
        为了加速查找，我们想到一个办法，把某封王通过一个关系转换，得到一个整数(即关键码值)，把该王信息保存在，以这个整数为下标的king_value[n]数组中，那么以后要查找任一个封王信息，只要把该王通过指定关系转换计算一下，就得到一个数组下标，很容易就得该王储存项，时间是固定的长度O(1)。这个转换关系就是哈希函数，这个数组就是哈希表。
         
        那么现在的问题是，如何实现这个转换关系，我们看看Linux内核的哈希函数

        点击(此处)折叠或打开

        1. unsigned long hash_long(unsigned long val,unsigned int bits)
        2. {
        3.         unsigned long hash = val * 0x9e370001UL;
        4.         return hash >> (32 - bits);
        5. }
        还有一个冲突问题，比如给英布用哈希函数得到整数10，就把king_value[10]就分给他了，那接着给刘季的哈希函数也得到10，怎么办呢，处理方法有开放地址法、再散列法、拉链法等。这里简单的放在11，若11已经有人占了，就给12，依次类推。
         
        那么内核这个哈希函数是否可以达到关键字均衡存放呢，写个简单的程序来测试下内核这个哈希函数是否靠谱，

        点击(此处)折叠或打开

        1. #include <stdio.h>
        2. #include <stdlib.h>
        3.  
        4. unsigned long hash_long(unsigned long val,unsigned int bits)
        5. {
        7.      unsigned long hash = val*0x9e370001UL;
        9.      return hash >> (32-bits);
        10. }
        12. int main(int argc, char *argv[])
        13. {
        14.      int i, j = atoi(argv[1]);
        16.      for (i = 0; i <= 32767; i++) {
        17.            if (hash_long(i, 11) == j)
        19.                 printf("pid-->%d ", hash_long(i,11));
        20.      }
        21.      return 0;
        22. }
        主要功能是把0～32767的pid值转换为hash的索引
         
        leon@PC:~/work$ ./a.out 10 |wc -l
        17
         
        leon @PC:~/work$ ./a.out 20 |wc -l
        17
         
        leon @PC:~/work$ ./a.out 23 |wc -l
        15
         
        leon @PC:~/work$ ./a.out 231 |wc -l
        17
         
        看看下标分配到0～2047出现的分布

        点击(此处)折叠或打开

        1. #!/bin/bash
        3. declare -i i
        5. i=0
        7. for((i=0;i<2047;i++))
        9. do
        11.          ./a.out $i | wc -l |tr 'n' ' '
        13. done
        leon@PC:~/work$ ./pid.sh
         
        18 17 17 17 16 15 15 15 15 17 17 17 17 15 15 15 15 16 17 17 17 17 15 15 15 14 17 17 17 17 17 15 15 15 15 17 17 17 17 16 15 15 14 15 17 17 17 17 16 15 15 15 16 17 17 17 17 16 15 14 15 16 17 17 17 17 15 15 15 15 17 17 17 17 17 15 14 15 15 17 17 17 17 16 15 15 15 15 17 17 17 17 16 14 15 15 16 17 17 17 17 16 15 15 15 16 17 17 17 17 14 15 15 15 16 17 17 17 17 15 15 15 15 17 17 17 17 15 15 15 15 15 17 17 17 18 15 15 15 15 16 17 17 17 17 15 15 15 15 16 17 17 18 16 15 15 15 15 16 17 17 17 16 15 15 15 15 17 17 18 17 16 15 15 15 15 17 17 17 17 15 15 15 15 16 17 18 17 17 15 15 15 15 16 17 17 17 16 15 15 15 15 16 18 17 17 16 15 15 15 15 17 17 17 17 16 15 15 15 15 18 17 17 17 15 15 15 15 15 17 17 17 17 15 15 15 15 17 17 17 17 16 15 15 15 14 17 17 17 17 16 15 15 15 16 17 17 17 17 16 15 15 14 16 17 17 17 17 15 15 15 15 16 17 17 17 17 15 15 14 15 17 17 17 17 17 15 15 15 15 17 17 17 17 16 15 14 15 15 17 17 17 17 16 15 15 15 16 17 17 17 17 15 14 15 15 16 17 17 17 17 15 15 15 15 17 17 17 17 17 14 15 15 15 17 17 17 17 16 15 15 15 15 17 17 17 17 15 15 15 15 16 17 17 17 18 15 15 15 15 16 17 17 17 16 15 15 15 15 17 17 17 18 16 15 15 15 15 17 17 17 17 15 15 15 15 15 17 17 18 17 15 15 15 15 16 17 17 17 17 15 15 15 15 16 17 18 17 16 15 15 15 15 16 17 17 17 16 15 15 15 15 17 18 17 17 15 15 15 15 15 17 17 17 17 15 15 15 15 16 18 17 17 17 15 15 15 15 16 17 17 17 16 15 15 15 15 17 17 17 17 16 15 15 15 15 17 17 17 17 16 15 15 15 16 17 17 17 17 15 15 15 14 17 17 17 17 17 15 15 15 15 17 17 17 17 16 15 15 14 15 17 17 17 17 16 15 15 15 16 17 17 17 17 16 15 14 15 16 17 17 17 17 15 15 15 15 16 17 17 17 17 15 14 15 15 17 17 17 17 17 15 15 15 15 17 17 17 17 16 14 15 15 16 17 17 17 17 16 15 15 15 16 17 17 17 17 14 15 15 15 16 17 17 17 17 15 15 15 15 17 17 17 17 16 15 15 15 15 17 17 17 18 15 15 15 15
         
        基本是均匀分布的，并且哈希函数及其简洁，实现了快速访问，典型的以空间换时间例子，堪称完美(原理还没弄明白)，要是项王看过Linux内核，懂得这水平的哈希函数，或许就不会有乌江惨剧了喔。

        关键词权重的量化方法TF/IDF - Loiy - ITeye技术网站 - Google Chrome (2013/8/7 22:19:00)

        关键词权重的量化方法TF/IDF

        博客分类： 
        搜索引擎算法工作 

        写这篇文章前，一定要说明一点，我对算法也是刚刚开始研究，一定会有不少地方会有差错，也请高手指正，上次计算相关度的方式发布后，就得到了高人的点化，在此谢谢这位高手，也谢谢大家对我的关注。

        下面进入主题：

        今天我想说的是关键词权重的量化方法TF/IDF，为什么说这个呢？因为我们知道，在数量庞大的搜索引擎库里，拥有无数个形容同一事物的词汇，就好像我上次说的手机和彩铃，他们分明是形容同一个类别：移动通讯相关的东西，但是谁的权重更高呢？这就看这个关键词所表达的意思和在具体文章中的意义来判断了。

        在搜索引擎中，一个词能够概括这篇文章意思的能力越高，权重就越高，反之则降低，举个例子吧，类似于这样的一个词：“吸烟的危害”，在这个词里面，吸烟是整个文章的一个主词，也就是说，吸烟这个词是整篇文章的核心，而“危害”这个词却能表达很多危害，例如环境污染危害，破坏公物的危害等。剩下的一个词“的”在整个句子里根本就没有任何意义，这样一来，我们的权重问题就可以看的很明白了，具体的权重大小就如下这样

        吸烟>危害>的，而“的”这个词因为不包含任何意义，所以，一般情况下，搜索引擎的计算规则中会讲“的”这个词消噪（这点纯属个人看法，请高手指教。）

        我们可以看到的是，有些词，只要你搜索一下，马上就会得出结果，例如吸烟 危害这样的词，而“的”这个词虽然存在于几乎所有的网页中，却根本不能反应出任何意义，这样一来他的权重就少的可怜了，这就是搜索引擎中的：“逆文本频率指数”（Inverse document frequency 缩写为IDF）他的计算公式是这样的，假如一个词W在DW个网页中出现过，那么DW的值越大，W的权重就越小。具体的公式如下log(D/dW).

        这个我们可以举个例子，假如有10亿个网页在搜索库里，而手机这个词出现的次数是两百万次，那么我们的计算公式就是

        log(2000000/1000000000)=log(500)=6.2

        通过这样的方式，我们就可以算出词的权重，这个办法，可以使用在优化当中的长尾生僻词的办法中，利用计算，得到最大的权重词，当然，你无法知道数据库里到底有多少个网页，因此，也就只能通过搜索结果来判断了，呵呵。

        那么TF是什么呢？

        TF是指你所选定关键词的出现频率，也就是单词汇的出现频率，（Term Frequency）举个例子，还是上面的例子，假如在一个有一千字的文章中“吸烟的危害”这几个词组在网页中分别出现以下的次数：

        吸烟：5次

        的：46次

        危害：9次

        这样，吸烟出现的频率是0.005%，“的”出现的频率是0.046，危害出现的频率是0.009%这样，结合相加，这个词“吸烟的危害”在这个文章中的比重就是0.06%。但是我们刚才说过，“的”这个词在大量网页中出现，而且根本无法形容任何意义，因此这个词是需要被删除的，那么，整个这个文章的关键词密度 就是（5+9）*100%，也就是仅仅0.016%。

        这个办法我们一般会使用在页面的关键词密度计算上，记住：类似“的”这样的词语是不能被作为关键词的，因为他会被忽略

        知道了以上的计算方法后，我们基本就可以知道搜索引擎是如何工作的了，但是有些朋友为了提高文章权重，大量的堆砌主关键词，也就是说假如“吸烟危害”是这个网页的关键词，他会为了提高排名而大量的堆砌关键词，其实根本没有必要去做，我在我的博客里曾经提到过一个“免费送Q币”的案例，他就完全避开了这样的限制，却做到了很好的排名，这就是一个关键词组合的办法，以后我会讲到，有兴趣的朋友可以去研究一下。

        接着我们的话题，TF/IDF被认为是信息检索中最伟大的发明，就是因为他在一定意义上解决了很多网页排序的问题，现在的大型搜索引擎都是靠这个公式去做为基础的，当然，在计算方式上会改进很多的部分，以求更准确，另外，结合向量空间模型（Vector Space Models） 、多文档列表求交计算等方式，使得搜索引擎的结果更加准确。

        写这篇小文的意思，主要是想让各位对搜索引擎的排序做一个深入的了解，上次我所说过的相关度与这篇文章也是息息相关的，大家不妨研究一下。

        本文原载：飘渺蝶舞的SEO梦想

        排重算法-odin2008-ChinaUnix博客 - Google Chrome (2013/8/7 19:58:19)

         排重算法 2008-06-10 17:18:12

        分类：

         

         

        1.1 信息指纹算法

        判断重复网页的思想：为每个网页计算出一组信息指纹（Fingerprint），若两个网页有一定数量相同的信息指纹，则认为这两个网页的内容重叠性很高，也就是说两个网页是内容复制的。

        判断内容复制的方法中最关键的两点：

        1、计算信息指纹（Fingerprint）的算法；

        2、判断信息指纹的相似程度的参数。

        信息指纹就是提取网页正文信息的特征，通常是一组词或者一组词＋权重，然后根据这组词调用特别的算法，例如MD5，将之转化为一组代码，这组代码就成为标识这个信息的指纹。从理论上讲，每两个不同文本的特征信息是不同的，那么得到的代码也应该是不一样的，就象人的指纹。

        得到预处理后的网页，然后对网页进行向量化处理，简单的讲就是分词，统计，并按照词频生成一个列表.

        例如：

        网页12

        搜索10

        引擎7

        ...

        ...

        然后取前N个关键词作为信息的矢量，例如：[网页12搜索10引擎7] 这是可以直接进行MD5哈系，或者按照其它规则进行重排后进行MD5哈系。例如本例，取前３个关键词，在进行哈系，得到的信息指纹就是：a7eb9d92a83cf438881915e0bc2df70b。

        这样a7eb9d92a83cf438881915e0bc2df70b 就作为本文档的指纹和以往的文档进行比较，如果有相同的，就说明指纹上看是一样的，就可以进入消重处理。至于关键词的权重，因为有众多的提取算法，比较常用的是nf/df。

        1.2 分段签名算法

        这种算法是按照一定的规则把网页切成N段，对每一段进行签名，形成每一段的信息指纹。如果这N个信息指纹里面有M个相同时（M是系统定义的阈值），则认为两者是复制网页。

        这种算法对于小规模的判断复制网页是很好的一种算法，但是对于像google这样海量的搜索引擎来说，算法的复杂度相当高。

        1.3 基于关键词的复制网页算法

        像google这类搜索引擎，他在抓取网页的时候都会记下以下网页信息：

        1、网页中出现的关键词（中文分词技术）以及每个关键词的权重（关键词密度）；

        2、提取meta descrīption或者每个网页的512个字节的有效文字。

        关于第2点，baidu和google有所不同，google是提取meta descrīption，没有查询关键字相关的512个字节，而百度是直接提取后者。

        在以下算法描述中，首先约定几个信息指纹变量：

         Pi表示第i个网页；

        该网页权重最高的N个关键词构成集合Ti={t1,t2,...tn}，其对应的权重为Wi={w1,w2,...wn}

        摘要信息用Des(Pi)表示，前n个关键词拼成的字符串用Con(Ti)表示，对这n个关键词排序后形成的字符串用Sort(Ti)表示。

        以上信息指纹都用MD5函数进行加密。

        基于关键词的复制网页算法有以下5种：

        1、MD5(Des(Pi))=MD5(Des(Pj)),就是说摘要信息完全一样，i和j两个网页就认为是复制网页；

        2、MD5(Con(Ti))=MD5(Con(Tj)),两个网页前n个关键词及其权重的排序一样，就认为是复制网页；

        3、MD5(Sort(Ti))=MD5(Sort(Tj)),两个网页前n个关键词一样，权重可以不一样，也认为是复制网页。

        4、MD5(Con(Ti))=MD5(Con(Tj))并且Wi-Wj的平方除以Wi和Wj的平方之和小于某个阙值a，则认为两者是复制网页。

        5、MD5(Sort(Ti))=MD5(Sort(Tj))并且Wi-Wj的平方除以Wi和Wj的平方之和小于某个阙值a，则认为两者是复制网页。

        关于第4和第5的那个阈值a,主要是因为前一个判断条件下，还是会有很多内容部分相同的网页被认为相同而被排除掉，因此要根据权重的分布比例调节a的大小。

        以上5种算法运行的时候，算法的效果取决于N，就是关键词数目的选取。选的数量越多，判断就会越精确，但是随之而来的计算速度也会减慢下来。所以必须考虑一个计算速度和去重准确率的平衡。据天网试验结果，10个左右关键词最恰当。

        1.4  随机映射(Random Projection)算法：

        先给每个词语(Token)生成随机的特征向量，保存为一个集合，然后对网页正文进行分词，得到一系列的词语，从词语的特征向量集合中取出这些词语的特征向量(如果词语不在在集合中，那么给词语生成一个随机的特征向量，将其加入集合)，将这些特征向量按位进行一个特殊的加运算，最后得到网页的特征向量。判断两个网页是否具有相似或重复内容就可以通过判断它们特征向量相同的位数(bit)来进行。

        1.5  近似网页发现算法

        首先，定义几个算法中用到的参数：

        Percentage：允许参与生成指纹的关键词的比例。

        Sum_interval：参与生成指纹的关键词个数的增长单位。

        算法如下：

        1、         对网页正文切词，生成网页正文的特征向量（已经去掉了停用词）

        2、         将向量中保留的关键词按照词频排序，相同词频的关键词按照字符排序（从大到小）。

        3、         在2中生成的关键词列表中选取前sum2 = sum1 * Percentage个关键词作为候选关键词。

        4、         在3中生成的关键词列表中选取前sum3 = sum2 DIV Sum_interval * Sum_interval个作为参与生成指纹的关键词集合。

        5、         将4中得到的关键词按照字符排序（从大到小），就得到了最终要生成指纹的字符串。

        6、         以5中生成的字符串为源串调用MD5函数得到该网页的指纹。

        指纹比较的过程中，只要对网页的指纹值直接排序就可以将重复的网页聚到一起。

        1.6

        1、对于每一个xml文件去标记，得到文本内容并进行分词，生成分词后的语料库C；

        2、 遍历语料库C，计算词语的IDF值；

        3、 对于每一篇文档，保留其idf值较大的前70%，并降序排列，构成该文档的特征向量；

        4、 计算任一文档的特征串的hash值，（拟用ELFhash），生成二元组<doc_id, hashvalue>。对具有相同hash值的文档，比较两个文档的特征串是否相同，如果相同，则是重合文档，否则不是重合文档。

        简单说明：

        a. hash函数的选择很关键，如果hash选择很好，时间复杂度为O（N）, N为文档规模 ，最坏情况下所有特征串的hash值相等，则时间复杂度是 O(N*N);

        b.我们添加了对同hash值文档的特征串进行比较，所以增加了时间复杂度；

        经过几天编程方法已经实现，本方法相对对重复的要求更严格，内容完全重复的一定可以识别，另外对Hash函数的选择也很关键；

        为了更好选择hash函数,做了以下实验，语料为1000个xml博客文件；

        实际重复文档数：419

        实际应该产生冲突数：419

        ELFHash产生冲突数： 594  所用时间为：60s

        RSHash产生冲突数：584    所用时间为：60S

        JSHash产生冲突数：546    所用时间为：58S

        PJWHash产生冲突数：594    所用时间为：61.4S

        BKDRHash产生冲突数：601   所用时间为：64.5S

        SDBMHash产生冲突数：546   所用时间为：61.5S

        DJBHas产生冲突数：  595   所用时间为：66S

        APHash产生冲突数：  543   所用时间为：57.1S

        经以上实验，选用了APHash函数来处理重复文档检测

         

        网页文本的排重算法介绍 - 李海波 -- 做影响一亿人的产品 - 博客频道 - CSDN.NET - Google Chrome (2013/8/7 14:10:49)

         

        网页文本的排重算法介绍

        分类： 1.自然语言处理/机器学习2010-09-15 16:59 1697人阅读 评论(0) 收藏 举报
        算法文档google搜索引擎random引擎
         

        目录(?)[+]

         

        转自http://hi.baidu.com/dobit/blog/item/87ef4eed8701c92d62d09f2b.html

        1.信息指纹算法

        判断重复网页的思想：为每个网页计算出一组信息指纹（Fingerprint），若两个网页有一定数量相同的信息指纹，则认为这两个网页的内容重叠性很高，也就是说两个网页是内容复制的。
        判断内容复制的方法中最关键的两点：
        1、计算信息指纹（Fingerprint）的算法；
        2、判断信息指纹的相似程度的参数。
        信息指纹就是提取网页正文信息的特征，通常是一组词或者一组词＋权重，然后根据这组词调用特别的算法，例如MD5，将之转化为一组代码，这组代码就成为标识这个信息的指纹。从理论上讲，每两个不同文本的特征信息是不同的，那么得到的代码也应该是不一样的，就象人的指纹。
        得到预处理后的网页，然后对网页进行向量化处理，简单的讲就是分词，统计，并按照词频生成一个列表.
        例如：
        网页12
        搜索10
        引擎7
        ...
        ...
        然后取前N个关键词作为信息的矢量，例如：[网页 12搜索10引擎7] 这是可以直接进行MD5哈系，或者按照其它规则进行重排后进行MD5哈系。例如本例，取前3个关键词，再进行哈希，得到的信息指纹就是：a7eb9d92a83cf438881915e0bc2df70b。这样a7eb9d92a83cf438881915e0bc2df70b 就作为本文档的指纹和以往的文档进行比较，如果有相同的，就说明指纹上看是一样的，就可以进入消重处理。至于关键词的权重，因为有众多的提取算法，比较常用的是nf/df。

        2.分段签名算法

        这种算法是按照一定的规则把网页切成N段，对每一段进行签名，形成每一段的信息指纹。如果这N个信息指纹里面有M个相同时（M是系统定义的阈值），则认为两者是复制网页。这种算法对于小规模的判断复制网页是很好的一种算法，但是对于像google这样海量的搜索引擎来说，算法的复杂度相当高。

        3.基于关键词的复制网页算法

        像google这类搜索引擎，他在抓取网页的时候都会记下以下网页信息：
        1、网页中出现的关键词（中文分词技术）以及每个关键词的权重（关键词密度）；
        2、提取meta descrīption或者每个网页的512个字节的有效文字。
        关于第2点，baidu和google有所不同，google是提取meta descrīption，没有查询关键字相关的512个字节，而百度是直接提取后者。
        在以下算法描述中，首先约定几个信息指纹变量：

        Pi表示第i个网页；
        该网页权重最高的N个关键词构成集合Ti={t1,t2,...tn}，其对应的权重为Wi={w1,w2,...wn}
        摘要信息用Des(Pi)表示，前n个关键词拼成的字符串用Con(Ti)表示，对这n个关键词排序后形成的字符串用Sort(Ti)表示。
        以上信息指纹都用MD5函数进行加密。
        基于关键词的复制网页算法有以下5种：
        1、MD5(Des(Pi))=MD5(Des(Pj)),就是说摘要信息完全一样，i和j两个网页就认为是复制网页；
        2、MD5(Con(Ti))=MD5(Con(Tj)),两个网页前n个关键词及其权重的排序一样，就认为是复制网页；
        3、MD5(Sort(Ti))=MD5(Sort(Tj)),两个网页前n个关键词一样，权重可以不一样，也认为是复制网页；
        4、MD5(Con(Ti))=MD5(Con(Tj))并且Wi-Wj的平方除以Wi和Wj的平方之和小于某个阙值a，则认为两者是复制网页；
        5、MD5(Sort(Ti))=MD5(Sort(Tj))并且Wi-Wj的平方除以Wi和Wj的平方之和小于某个阙值a，则认为两者是复制网页；
        关于第4和第5的那个阈值a,主要是因为前一个判断条件下，还是会有很多内容部分相同的网页被认为相同而被排除掉，因此要根据权重的分布比例调节a的大小。
        以上5种算法运行的时候，算法的效果取决于N，就是关键词数目的选取。选的数量越多，判断就会越精确，但是随之而来的计算速度也会减慢下来。所以必须考虑一个计算速度和去重准确率的平衡。据天网试验结果，10个左右关键词最恰当。

        4.随机映射(Random Projection)算法：

        先给每个词语(Token)生成随机的特征向量，保存为一个集合，然后对网页正文进行分词，得到一系列的词语，从词语的特征向量集合中取出这些词语的特征向量(如果词语不在在集合中，那么给词语生成一个随机的特征向量，将其加入集合)，将这些特征向量按位进行一个特殊的加运算，最后得到网页的特征向量。判断两个网页是否具有相似或重复内容就可以通过判断它们特征向量相同的位数(bit)来进行。

        5.近似网页发现算法

        首先，定义几个算法中用到的参数：
        Percentage ：允许参与生成指纹的关键词的比例。
        Sum_interval ：参与生成指纹的关键词个数的增长单位。
        算法如下：
        1、对网页正文切词，生成网页正文的特征向量（已经去掉了停用词）
        2、将向量中保留的关键词按照词频排序，相同词频的关键词按照字符排序（从大到小）。
        3、在2中生成的关键词列表中选取前sum2 = sum1 * Percentage个关键词作为候选关键词。
        4、在3中生成的关键词列表中选取前sum3 = sum2 DIV Sum_interval * Sum_interval个作为参与生成指纹的关键词集合。
        5、将4中得到的关键词按照字符排序（从大到小），就得到了最终要生成指纹的字符串。
        6、以5中生成的字符串为源串调用MD5函数得到该网页的指纹。
        指纹比较的过程中，只要对网页的指纹值直接排序就可以将重复的网页聚到一起。

        6.Hash算法

        1、对于每一个xml文件去标记，得到文本内容并进行分词，生成分词后的语料库C；
        2、遍历语料库C，计算词语的IDF值；
        3、对于每一篇文档，保留其idf值较大的前70%，并降序排列，构成该文档的特征向量；
        4、计算任一文档的特征串的hash值，（拟用ELFhash），生成二元组<doc_id, hashvalue>。对具有相同hash值的文档，比较两个文档的特征串是否相同，如果相同，则是重合文档，否则不是重合文档。

        简单说明：
        a. hash函数的选择很关键，如果hash选择很好，时间复杂度为O（N）, N为文档规模，最坏情况下所有特征串的hash值相等，则时间复杂度是 O(N*N);
        b.我们添加了对同hash值文档的特征串进行比较，所以增加了时间复杂度；经过几天编程方法已经实现，本方法相对对重复的要求更严格，内容完全重复的一定可以识别，另外对Hash函数的选择也很关键；为了更好选择hash函数,做了以下实验，语料为1000个xml博客文件；

        实际重复文档数：419
        实际应该产生冲突数：419
        ELFHash产生冲突数： 594 所用时间为：60s
        RSHash产生冲突数：584 所用时间为：60S
        JSHash产生冲突数：546 所用时间为：58S
        PJWHash产生冲突数：594 所用时间为：61.4S
        BKDRHash产生冲突数：601 所用时间为：64.5S
        SDBMHash产生冲突数：546 所用时间为：61.5S
        DJBHas产生冲突数： 595 所用时间为：66S
        APHash产生冲突数： 543 所用时间为：57.1S
        经以上实验，选用了APHash函数来处理重复文档检测

        7.一般处理的方法

        （1）最原始的使用文本相似度判别，相当准确，但是计算速度慢，提高的方法无非是先索引进行预处理，或者用SVD来降维减少矩阵运算时间
        （2）文本摘要为文本特征，进行特征重复判别
        （3）抽取文本关键词，构成比较小的文本向量做为特征进行判别
        大家考虑过以上3中算法的共性没？那就是要分词，中文分词博大精深，效果越好速度越慢这是铁律，但具体还要看分词算法的设计。所以这部分时间的消耗以上3中方法是无可避免的必须进行的步骤。

        8.基于句子的方式

        而我所考虑的是从句子的角度，但如果单个句子的特征，特征未免单一，而不具有代表性，句子多了又可能，造成特征过于复杂和容错性能的下降，毕竟我们通过自动抽取的网页正文不能保证100%无任何噪音和抽取失误带来的原文缺失。在这个角度上我们进一步考虑是否能有更好的方法呢？传统中文断句，我们主要依赖于标点符号，那我的想法就是标点符号左右的汉字已经能有很强的代表性来作为句子的特征，而句子又能作为文本的特征，因此尝试了取逗号 句号 感叹 问号 左右2边各2个汉字或英文作为特征，来进行文本表示。


        全文按照标点符号取出汉字后构成了1个比较长的串，但为了信息指纹的需要，我们必须考虑容错性的问题，这个串如果直接HASH，有可能因为噪音的加入产生巨大的偏差，因此我对这个长串做了截断的处理，同时考虑一般标题的信息含量很高，单独认为标题也成为1个字串，指纹特征就变成了1个标题的HASH码 3个截断后的子串HASH码 同时标题的权重为1.5 其他子串权重为1.0 阀值设定为3 这样如果有标题相同 并有2个字串相同的文章我们就认为是重复，或者标题不相同 3个字串完全相同的是重复。具体消重特征判别，是使用数据库的内存表还是BLOOMFILTER之类的算法就随便你了。


        当然以上算法的前提是正文和标题抽取的准确如果噪音过多，这个算法可能降低到一个完全无法应用的程度，怎么提高该算法的在噪音比较高情况下的容错性，该是自己考虑的问题了。

        9.我的一些想法

        需要排除重复文本有如下几种：1.绝大部分一样（比如转载）；2.部分一样（修修改改）；3.话题一样（聚类范畴）。

        上面各种方法：

        1）一种是有序的如2，8；另一种是无序的，如1，3，4，5，6，按照特征权重排序；

        2）特征值的生成有三种，MD5，按位加，哈希。

        基于段落和句子的有序算法，可能会漏排；而基于特征的算法可能会误排。

        既然是网页文本排重，可以把网页的信息考虑进去：比如

        [xhtml] view plaincopy
        1. <title>最高法：用人单位隐匿加班证据应该担责_新闻中心_新浪网</title>  
        2. <meta name=keywords content="最高法：用人单位隐匿加班证据应该担责,加班费">  
        3. <meta name=description content="最高法：用人单位隐匿加班证据应该担责">   

        可以根据title，keywords,description等信息获取核心词指纹（核心词可以是几个，方法参考上面的方法），再获取内容的分段（可以把小的段合并，再取最大的几段）指纹。先比较核心词指纹，如果一样，则比较内容指纹；如果核心词不一样，则直接排除。这个方法只用核心词，而不是整个标题，可以容忍标题噪音，用核心词做一次粗排，再用精确指纹进行细排；第一次核心词指纹查找可以排除大量不相干的网页（毕竟重复的比重还是比较低的），只是从近似网页（近似网页少很多）中查找分段指纹，计算效率上有保证，比如1亿网页，和当前文本核心词一样的比如只有1万，则分段指纹只需要比较1万个。

        后记：

        SimHash算法可以用来排重：

        simhash算法的原理

        http://www.cnblogs.com/linecong/archive/2010/08/28/simhash.html

        利用simhash来进行文本去重复

        http://blog.csdn.net/fuyangchang/archive/2010/06/01/5639595.aspx

        SimHash算法可以用来排重，但是SimHash的特征取值，同样需要处理，因为网页排重不是比较两个网页源文件是否重复，而是比较其内容是否重复，所以，必须进行去噪和提取特征的步骤。

        其实排重分为两步

        1、是特征的选择，选择什么样的特征来代表整个网页

        2、特征的计算，MD5、Hash等算法

        我认为第1个是难点。

        Google字符串模糊匹配算法，字典树模糊查询 - Belong to Sopranos - 博客频道 - CSDN.NET - Google Chrome (2013/8/6 21:50:33)

        Google字符串模糊匹配算法，字典树模糊查询

        分类： 数据结构 算法相关2010-05-15 16:43 7803人阅读 评论(2) 收藏 举报
        算法googlestringdelete输入法struct

        好吧，我承认我又装13标题党了。其实是G查询关键词过程中匹配的一点大概的算法框架，G的模糊匹配大家都知道，比如你输入64什么的，G会自动列出你心里可能要找

        到东西，如下图:

        那这个算法是怎么实现的呢，用到了一种高级数据结构--字典树，或者说是字典树思想，因为字典树不规定你具体怎么实现，可以二维数组，可以map……也可以通常的结构体+next指针。可以通过一个题来讲述，就是2009ACM/ICPC 哈尔滨 reginal现场赛G题：Fuzzy Google Suggest（http://acm.hit.edu.cn/judge/show.php?Proid=2888&Contestid=0）讲解。当时我搞这题，不知道字典树，然后一直模拟，结果……(— —|||)先用输入的单词构造一棵字典树，节点数据包括：cnt，表示节点上的字母被多少个单词经过；vis，0表示经过此节点不能继续匹配，1表示经过此节点可继续匹配，2表示此节点就是恰好用于匹配的前缀的最后一个字符；然后一个next数组，大小26，但不是node指针，而是int数组，表示当前节点的儿子，next[i]==-1表示当前节点没有第i个儿子，否则有，并将此儿子结点进行编号，其编号就是它在字典树中的编号。然后根据编辑距离进行dfs遍历；函数设计为dfs(int x,int pos,intedit,char* key),x是trie树中第x个节点，pos表示匹配到了前缀字符key的第pos个字符，edit表示剩余可用的编辑距离。假如某个字符符合当前前缀的匹配条件，则trie节点向儿子结点递归，pos++，edit不变dfs(root[x].next[key[pos]-'a'],++pos,edit,key)；否则尝试使用编辑距离：1，增加一个字符，此时要遍历26个字符，看增加哪个合法（即此字符在trie中出现了并且是当前key[pos]的儿子节点并且此字符不跟key[pos]相同），然后继续dfs,此时编辑距离少一个，key的位置不变，trie走向儿子节点，假设增加的字符编号为i，则dfs(root[x].next[i],++pos,edit-1,key)；2，替换一个字符，此时edit减一，pos向前走一个，dfs(root[x].next[i],pos+1,edit-1,key);3,删除一个字符，删除表示为trie节点不变，但是前缀字符串key串往下走一个，相当于就没匹配上的忽略，dfs(x,pos+1,edit-1,key),若能遍历下去，且x节点之前不可通行，则将x标记为可通行.到达匹配终点的条件有三个：1，前缀串key一路匹配到了末尾，此时的结点x被标记为，root[x].vis=2,表示它是某个前缀串的终结者。2，在tire中一路通行突然edit用完透支了，那这个前缀串没有找到匹配的单词，回溯。3，碰到了某个节点x,root[x].vis=2,说明到x这个前缀串已经能够匹配。返回可以匹配。然后再利用dfs_calc函数计数符合匹配的单词数量:vis=2的结点。最后用dfs_clear()函数清理trie树。关于销毁trie树，见有人用一个for循环搞定的，那样只是把和根节点直接相连的结点进行了delete，但是其他的都变成悬空状态，并未被销毁。坏习惯(但对ACM题来说不失为一种销毁的捷径)。不过用struct写的交上去老是RE，极度掣肘，只好参看某牛的改作数组实现的trie：
        RE的：

        [cpp] view plaincopy
        1. #include<pzjay>  
        2. #<一坨头文件>  
        3. const int sup=500005;  
        4. int tot;//tire结点个数  
        5. int len;//记录前缀词 的长度  
        6. int ans;//记录此前缀匹配单词的个数  
        7. struct node  
        8. {  
        9.     int cnt;//表示此字母被多少个单词经过  
        10.     int vis;//vis=0表示经过此单词不能够到达要匹配的结点;1表示可以;2表示此字母就是匹配前缀的最后一个字母(即匹配完毕)  
        11.     int next[26];  
        12. }root[sup];  
        13. void creat(char key[])  
        14. {  
        15.     int i=0,index;  
        16.     int k=1;//root下标  
        17.     while(key[i])  
        18.     {  
        19.         index=key[i]-'a';  
        20.         if(-1==root[k].next[index])  
        21.         {  
        22.             root[k].next[index]=tot;//将root[tot]的地址赋给tmp->next[index]  
        23.             root[tot].cnt=1;  
        24.             root[tot].vis=0;  
        25.             ++tot;  
        26.         }  
        27.         else  
        28.             ++root[root[k].next[index]].cnt;  
        29.         k=root[k].next[index];  
        30.         ++i;  
        31.     }  
        32. }  
        33. int dfs(int x,int pos,int edit,char* key)//返回是否成功匹配  
        34. {  
        35.     if(2==root[x].vis)//到达一个匹配的结束点  
        36.         return 1;  
        37.     if(edit<0)  
        38.         return 0;  
        39.     if(pos==len)//到达前缀的末尾  
        40.     {  
        41.         root[x].vis=2;//该节点是前缀的结束字母，x之前的单词串被成功匹配  
        42.         return 1;  
        43.     }  
        44.     int index=key[pos]-'a';  
        45.     if(-1!=root[x].next[index])//还有儿子结点  
        46.         if(dfs(root[x].next[index],pos+1,edit,key))  
        47.             root[x].vis=1;  
        48.     for(int i=0;i<26;++i)  
        49.     {  
        50.         index=key[pos]-'a';  
        51.         if(index==i || -1==root[x].next[i])//在树中找可替换的字符  
        52.             continue;  
        53.         if(dfs(root[x].next[i],pos+1,edit-1,key))//将pos处的字母尝试用i+'a'代替  
        54.             root[x].vis=1;  
        55.         if(dfs(root[x].next[i],pos,edit-1,key))//插入一个字母  
        56.             root[x].vis=1;  
        57.     }  
        58.     if(dfs(x,pos+1,edit-1,key))//delete  
        59.         if(0==root[x].vis)  
        60.             root[x].vis=1;  
        61.     return root[x].vis;  
        62. }  
        63. void dfs_calc(int x)  
        64. {  
        65.     if(2==root[x].vis)  
        66.     {  
        67.         ans+=root[x].cnt;  
        68.         return;  
        69.     }  
        70.     for(int i=0;i<26;++i)  
        71.         if(root[root[x].next[i]].vis > 0)  
        72.             dfs_calc(root[x].next[i]);  
        73. }  
        74. void dfs_clear(int x)  
        75. {  
        76.     root[x].vis=0;  
        77.     for(int i=0;i<26;++i)  
        78.         if(root[root[x].next[i]].vis > 0)  
        79.             dfs_clear(root[x].next[i]);  
        80. }  
        81. int main()  
        82. {  
        83.     int n;  
        84.     //freopen("1.txt","r",stdin);  
        85.     while(scanf("%d",&n)!=EOF)  
        86.     {  
        87.         tot=2;  
        88.         char key[25];  
        89.         int m;  
        90.         int edit;//编辑距离  
        91.         for(int i=0;i<sup;++i)  
        92.             memset(root[i].next,-1,sizeof(root[i].next));  
        93.         //fill(root[i].next,root[i].next+26,-1);  
        94.         while(n--)  
        95.         {  
        96.             scanf("%s",key);  
        97.             creat(key);  
        98.         }  
        99.         scanf("%d",&m);//m个前缀  
        100.         while(m--)  
        101.         {  
        102.             ans=0;  
        103.             scanf("%s %d",key,&edit);  
        104.             len=strlen(key);  
        105.             dfs(1,0,edit,key);  
        106.             //1是x的起始遍历位置，0是前缀key的起始位置，edit是剩余的编辑距离  
        107.             dfs_calc(1);//计数符合匹配的单词个数  
        108.             dfs_clear(1);//清空x  
        109.             printf("%d/n",ans);  
        110.         }  
        111.     }  
        112.     return 0;  
        113. }  
        114.   
        115. AC：  
        116. const int sup=700005;  
        117. int tot;//tire结点个数  
        118. int len;//记录前缀词 的长度  
        119. int ans;//记录此前缀匹配单词的个数  
        120. int root[sup][26];//每个节点最多26个分支  
        121. int cnt[sup],vis[sup];//cnt[i]记录字母i被多少个单词经过  
        122. void creat(char key[])  
        123. {  
        124.     int k=1,index,i=0;  
        125.     while(key[i])  
        126.     {  
        127.         index=key[i]-'a';  
        128.         if(-1==root[k][index])  
        129.             root[k][index]=tot++;  
        130.         k=root[k][index];  
        131.         ++cnt[k];  
        132.         ++i;  
        133.     }  
        134. }  
        135. int dfs(int x,int pos,int edit,char key[])  
        136. {  
        137.     if(2==vis[x])  
        138.         return 1;  
        139.     if(edit<0)  
        140.         return 0;  
        141.     if(pos==len)//匹配完毕，节点x成为前缀词key的结尾字母  
        142.     {  
        143.         vis[x]=2;  
        144.         return  1;  
        145.     }//以上可以直接return的，都是最终的结果:匹配成功或者失败  
        146.     //下面的只是递归到最重结果的过程，故是对vis赋值  
        147.     int index=key[pos]-'a';  
        148.     if(-1!=root[x][index])//可以继续往深层遍历  
        149.         if(dfs(root[x][index],pos+1,edit,key))  
        150.             vis[x]=1;//从x往下可以走到目标节点  
        151.     for(int i=0;i<26;++i)  
        152.     {  
        153.         index=key[pos]-'a';  
        154.         if(index==i || -1==root[x][i])//筛选掉跟要替换的字母相同的字母和未在trie树中出现的字母  
        155.             continue;  
        156.         if(dfs(root[x][i],pos+1,edit-1,key))//pos++，遍历下一个字母，表示替换一个trie树中存在的字母  
        157.                 vis[x]=1;  
        158.         if(dfs(root[x][i],pos,edit-1,key))//pos不变.表示增加一个字母  
        159.                 vis[x]=1;  
        160.     }  
        161.     if(dfs(x,pos+1,edit-1,key))//删除一个字母  
        162.         if(0==vis[x])  
        163.             vis[x]=1;  
        164.     return vis[x];  
        165. }  
        166. void dfs_calc(int x)  
        167. {  
        168.     if(2==vis[x])  
        169.     {  
        170.         ans+=cnt[x];  
        171.         return;  
        172.     }  
        173.     for(int i=0;i<26;++i)  
        174.         if(vis[root[x][i]])  
        175.             dfs_calc(root[x][i]);  
        176. }  
        177. void dfs_clear(int x)  
        178. {  
        179.     vis[x]=0;  
        180.     for(int i=0;i<26;++i)  
        181.         if(vis[root[x][i]])  
        182.             dfs_clear(root[x][i]);  
        183. }  
        184. int main()  
        185. {  
        186.     int n;  
        187.       
        188.     char key[16];  
        189.       
        190.     while(scanf("%d",&n)!=EOF)  
        191.     {  
        192.         int edit,m;  
        193.         memset(root,-1,sizeof(root));  
        194.         memset(vis,0,sizeof(vis));  
        195.         memset(cnt,0,sizeof(cnt));  
        196.         tot=2;  
        197.         while(n--)  
        198.         {  
        199.             scanf("%s",key);  
        200.             creat(key);  
        201.         }  
        202.         scanf("%d",&m);  
        203.         while(m--)  
        204.         {  
        205.             ans=0;  
        206.             scanf("%s %d",key,&edit);  
        207.             len=strlen(key);  
        208.             dfs(1,0,edit,key);  
        209.             dfs_calc(1);  
        210.             printf("%d/n",ans);  
        211.             dfs_clear(1);  
        212.         }  
        213.     }  
        214.     return 0;  
        215. }参看：http://acmicpc.org.cn/wiki/index.php?title=2009_Harbin_Fuzzy_Google_Suggest_Solution  
        216.   
        217. ps:转载注明出处：pzjay！  

        除了模糊匹配外还有精确匹配，金山词霸手机版E文输入，T9输入法等许多优秀的手机E文输入软件都采用了精确匹配。以T9输入法为例，它摒弃传统的输入按键模式，假如你想输入ccc，传统的是要摁3*3=9下2键，但是假如ccc是经常使用的高频词汇的话，T9输入法只摁三下即可。牵扯到频率，肯定又是字典树的应用了，题目相关：HDOJ1298
        本题先输入一个单词表，包括单词以及该单词的权值。然后输入一些数字串，要求模拟手机输入的过程，每输入一个数字，就输出对应的单词（如果没有对应的就输出        MANUALLY），如果输入的数字会对应不同的单词的前缀，就输出权值之和最高的前缀（如果权值一样就按字母表顺序）。用Sample来说明，输入了hell，hello，idea这3个单词，权值对应分别为3,4,8，开始输入数字：输入4，4可以对应i和h，i是idea的前缀，权值之和为8，h是hell和hello的前缀，权值之和是3+4=7，输出权值较大的i；继续输入3,43对应的可以是he和id，同样因为id的权值大于he，就输出id；接下来输入5,435就只能对应hel了……依此类推，每次输出的都是权值之和最高的词
        思想：trie+BFS
        算法流程：
        1。根据输入的单词建树
        2。根据输入的按键序列依次转化为可能的字符序列，维护一个双端队列，将树中出现过(通过查找字典树实现)的字符序列入列，用于下次增加字符序列
        3。若当前枚举到的按键序列遍历完所有可能后若最大权值还是-1，说明该按键序列没有匹配的字符串；否则输出权值最大的字符串即可。注意若字符序列中间出现不匹        配，那么以后的都不匹配，但此时仍然要继续遍历依次输出不匹配，不能退出。见过HH大神map实现trie树的代码，很好很强大。(map <string,int>表示string出现的频率int)

        [cpp] view plaincopy
        1. #include<iostream>  
        2. #include<一坨头文件>  
        3. #include<转载注明pzjay原创>  
        4. const int sup=100;  
        5. int num[10];//num[i]表示第i个键上面的字母个数  
        6. char T9[10][4];//T9[i][j]表示第i个键上第j个字母  
        7. deque <string> dq;  
        8. int n;  
        9. struct node  
        10. {  
        11.     int count;//记录出现次数  
        12.     node* next[26];  
        13.     node(int fre)  
        14.     {  
        15.         count=fre;  
        16.         memset(next,NULL,sizeof(next));  
        17.     }  
        18. };  
        19. node* root;  
        20. void creat(char key[],int freq)  
        21. {  
        22.     int i=0,index;  
        23.     node* tmp=root;  
        24.     while(key[i])  
        25.     {  
        26.         index=key[i]-'a';  
        27.         if(NULL==tmp->next[index])  
        28.             tmp->next[index]=new node(freq);  
        29.         else  
        30.             tmp->next[index]->count+=freq;  
        31.         tmp=tmp->next[index];  
        32.         ++i;  
        33.     }  
        34. }  
        35. int find(string key)  
        36. {  
        37.     int i=0,index;  
        38.     node* tmp=root;  
        39.     while(i<key.length())  
        40.     {  
        41.         index=key[i]-'a';  
        42.         if(NULL==tmp->next[index])  
        43.             return -1;  
        44.         tmp=tmp->next[index];  
        45.         ++i;  
        46.     }  
        47.     return tmp->count;//返回权值  
        48. }  
        49. void init()  
        50. {  
        51.     int i,j;  
        52.     char tmp='a';  
        53.     for(i=2;i<10;++i)  
        54.         num[i]=3;  
        55.     ++num[7];  
        56.     ++num[9];//第7和9个按键上各4个字母  
        57.     for(i=2;i<10;++i)  
        58.         for(j=0;j<num[i];++j)  
        59.             T9[i][j]=tmp++;  
        60. }  
        61. void dele()//删除字典树  
        62. {  
        63.     for(int i=0;i<26;++i)  
        64.         if(root->next[i])  
        65.             delete root->next[i];  
        66.     delete root;  
        67. }  
        68. int main()  
        69. {  
        70.     init();//初始化数组  
        71.     char key[110];  
        72.     int Case;  
        73.     scanf("%d",&Case);  
        74.     char tmp;  
        75.     int frequency;  
        76.     string str;  
        77.     for(int pzjay=1;pzjay<=Case;++pzjay)  
        78.     {  
        79.         root=new node(0);  
        80.         scanf("%d",&n);  
        81.         while(n--)  
        82.         {  
        83.             scanf("%s %d",key,&frequency);  
        84.             creat(key,frequency);  
        85.         }  
        86.         scanf("%d",&n);  
        87.         int id;  
        88.         string head;  
        89.         string ans;  
        90.         int max_frequency;  
        91.         printf("Scenario #%d:/n",pzjay);  
        92.         int increment,size;  
        93.         while(n--)  
        94.         {  
        95.             scanf("%s",key);  
        96.             size=1;//初始队列中一个元素  
        97.             while(!dq.empty())  
        98.                 dq.pop_back();  
        99.             dq.push_back("");//首先压入双端队列一个空字符串  
        100.             //转载注明出处:pzjay  
        101.             for(int i=0;key[i]!='1';++i)  
        102.             {  
        103.                 id=key[i]-'0';//将按键转化为数字  
        104.                 increment=0;  
        105.                 max_frequency=-1;  
        106.                 for(int k=0;k<size;++k)  
        107.                 {  
        108.                     head=dq.front();//或者dq[0]也可  
        109.                     dq.pop_front();  
        110.                     for(int j=0;j<num[id];++j)  
        111.                     {  
        112.                         str=head+T9[id][j];  
        113.                         int value=find(str);  
        114.                         if(-1!=value)//找到了  
        115.                         {  
        116.                             dq.push_back(str);  
        117.                             ++increment;//记录本次新增了多少个元素，本次新增的元素就是下次拓展的起点  
        118.                             if(value > max_frequency)  
        119.                             {  
        120.                                 max_frequency=value;  
        121.                                 ans=str;  
        122.                             }  
        123.                         }     
        124.                     }  
        125.                 }  
        126.                 size=increment;  
        127.                 if(max_frequency!=-1)  
        128.                     printf("%s/n",ans.c_str());  
        129.                 else  
        130.                     printf("MANUALLY/n");//其实这时可以退出for了，不过继续遍历也无妨，因为中间断掉，后面的肯定都不行  
        131.             }  
        132.             printf("/n");  
        133.         }  
        134.         printf("/n");  
        135.         dele();  
        136.     }  
        137.     return pzjay;  
        138. }  
        139. 字典树容易理解，用处广泛并且本文pzjay原创，— —|||  
      • 相关阅读:
        Spring Boot----整合SpringCloud
        python apscheduler学习
        Java8 Lambda
        Java Json操作
        python 环境相关
        大数据 Hadoop 单机版安装
        大数据 CDH 6.2 安装
        Java8 时间API
        python 字符串方法
        《JavaScript高级程序设计》笔记——第一章到第三章
      • 原文地址：https://www.cnblogs.com/stlong/p/6289112.html
      Copyright © 2011-2022 走看看