前言
\(\color{red}{\texttt{WYCdalao}}\)在\(1.542\)年之前切的题现在才写掉\(qwq\),\(\color{grey}{\texttt{stoorz}}\)怕不是要被\(\color{red}{\texttt{WYCdalao}}\)碾爆\(qwqwq\)。
\[\color{white}{\texttt{上图不可以点QWQ}}
\]
题目
克里特岛以野人群居而著称。岛上有排列成环行的M个山洞。这些山洞顺时针编号为1,2,…,M。岛上住着N个野人,一开始依次住在山洞C1,C2,…,CN中,以后每年,第i个野人会沿顺时针向前走Pi个洞住下来。
每个野人i有一个寿命值Li,即生存的年数。
下面四幅图描述了一个有6个山洞,住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为1,2,3;每年要走过的洞穴数依次为3,7,2;寿命值依次为4,3,1。
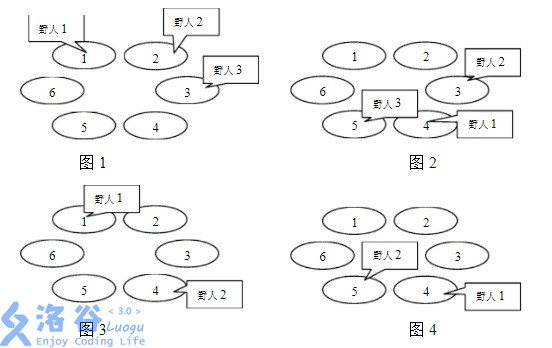
奇怪的是,虽然野人有很多,但没有任何两个野人在有生之年处在同一个山洞中,使得小岛一直保持和平与宁静,这让科学家们很是惊奇。他们想知道,至少有多少个山洞,才能维持岛上的和平呢?
思路
这道题的实际数据范围是\(1\le n\le 15\),\(1\le C_i,P_i\le 100\),\(0\le L_i\le 10^6\)。
其实题目说了那么多,题意其实就是给出\(c_i,p_i,l_i\),求一个最小的\(m\)使得所有方程组
\[\left\{\begin{matrix}c_i+xp_i\equiv c_j+xp_j\ (\rm{mod}\ m)
\\ x\leq l_i
\\ x\leq l_j
\end{matrix}\right.\]
无解。
由于\(m\)较小而且题目保证一定存在一个\(m\leq 10^6\)的解。所以考虑枚举\(m\),然后枚举每一个野人。
\[c_i+xp_i\equiv c_j+xp_j\ (mod\ m) \Leftrightarrow (p_i-p_j)x+m·y=x_j-c_i
\]
我们发现可以用\(Exgcd\)来求出满足要求的\(x\)。
那么要使得上述方程组无解,必须满足一下条件之一:
- \(c_j-c_i\)不是\(gcd(p_i-p_j,m)\)的倍数
- 求出来的\(x>min(l_i,l_j)\)
时间复杂度\(O(mn^2\log p_i)\)。
代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=20;
int n,m,c[N],p[N],l[N];
bool flag;
int exgcd(int a,int b,int &x,int &y)
{
if (!b)
{
x=1; y=0;
return a;
}
int d=exgcd(b,a%b,x,y);
int temp=x; x=y; y=temp-a/b*y;
return d;
}
void check(int i,int j)
{
if (p[i]<p[j]) swap(i,j);
int x,y,d=exgcd(p[i]-p[j],m,x,y);
if ((c[j]-c[i])%d) return;
x=(x*(c[j]-c[i])/d%(m/d)+(m/d))%(m/d);
if (x<=min(l[i],l[j])) flag=0;
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
scanf("%d%d%d",&c[i],&p[i],&l[i]);
m=max(m,c[i]);
}
for (;;m++)
{
flag=1;
for (int i=1;i<=n && flag;i++)
for (int j=i+1;j<=n && flag;j++)
check(i,j);
if (flag) return !printf("%d",m);
}
printf("WYC AK IOI OrzOrz");
return 0;
}
