【GMOJ5057】炮塔

题目

题目链接：https://gmoj.net/senior/#main/show/5057
A 君正在玩一款战略游戏，游戏中的规则是这样的：
给定一个 (n imes m) 的地图，地图上每一个位置要么是空地，要么是炮塔，要么有若干数量的敌人。现在 A 君要操控炮塔攻击这些敌人。
对于每个炮塔，它们的攻击方向已经确定(上下左右其中一个)，A 君只需要为每个炮塔指定攻击位置。每一个炮塔只能朝它攻击方向上的某个位置进行攻击，每个炮塔只能攻击一次，当然，炮塔也可以不进行攻击。炮塔对一个位置攻击后，位置上的所有敌人都会被消灭。
现在，游戏已经保证不存在一个炮塔能够攻击另一个炮塔的情况。但是，若把炮塔的位置与其攻击位置间的连线称为炮弹的运行轨迹，那么A君的攻击方案要保证不存在两条轨迹相交。
在端点处(即攻击了同一个位置)也算相交，下图是一个相交的例子:

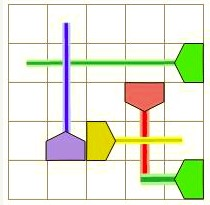
思路

考虑网络流。因为有路径不能相交的限制，所以我们考虑构造一种网络图使得如果两条路线有交，那么就必然存在源点到汇点的一条路径。这样整张图的最小割就是我们强制炮塔路径不交时，必须割掉的边。
将行和列分开来建图，假设现在在建行的图，记 (f[i][j]) 表示格子 ((i,j)) 到第 (i) 行能攻击到它的炮塔的路径中，敌人最多的格子的敌人数量。
那么考虑以下建图（黄色是炮塔，蓝色是敌人）

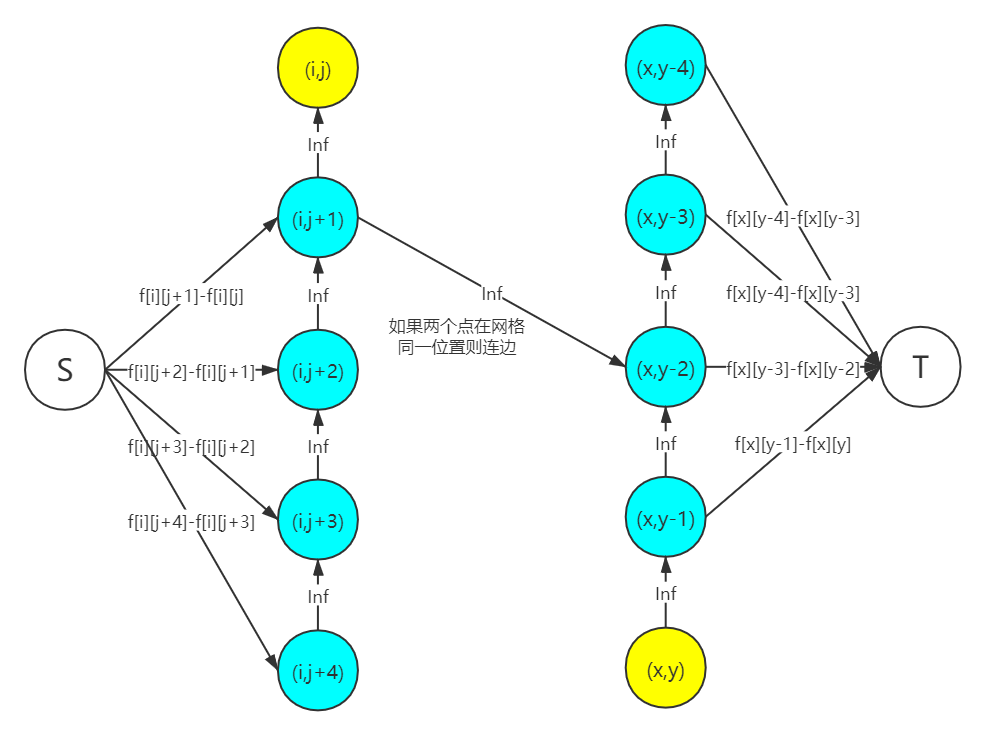
上图中 ((i,j+1)) 与 ((x,y-2)) 是网格中同一个点，所以我们必须要割掉左右两条边的一个。这样就等价于要让一个炮塔的打不到这个格子。假设割掉右边的边，那么右边的炮塔等价于最多打到 ((x,y-1))。然后它所得到的价值等于它能打到的位置的敌人最大值。
这是一个最大权闭合子图的模型，让除去 (+infty) 的边权之和减去最大流即可。

代码

#include <bits/stdc++.h>
using namespace std;

const int N=55,M=5010,Inf=1e9;
const int dx[]={0,-1,1,0,0},dy[]={0,0,0,-1,1};
int n,m,S,T,tot,maxf,a[N][N],head[M],cur[M],dep[M];

int ID(int x,int y,int k)
{
	return (x-1)*m+y+k*n*m;
}

struct edge
{
	int next,to,flow;
}e[M*8];

void add(int from,int to,int flow)
{
	e[++tot].to=to;
	e[tot].flow=flow;
	e[tot].next=head[from];
	head[from]=tot;
}

bool bfs()
{
	memcpy(cur,head,sizeof(head));
	memset(dep,0x3f3f3f3f,sizeof(dep));
	queue<int> q; q.push(S);
	dep[S]=0;
	while (q.size())
	{
		int u=q.front(); q.pop();
		for (int i=head[u];~i;i=e[i].next)
		{
			int v=e[i].to;
			if (e[i].flow && dep[v]>Inf)
			{
				dep[v]=dep[u]+1;
				q.push(v);
			}
		}
	}
	return dep[T]<Inf;
}

int dfs(int x,int flow)
{
	if (x==T) return flow;
	int res,used=0;
	for (int i=cur[x];~i;i=e[i].next)
	{
		cur[x]=i;
		int v=e[i].to;
		if (e[i].flow && dep[v]==dep[x]+1)
		{
			res=dfs(v,min(e[i].flow,flow-used));
			used+=res;
			e[i].flow-=res; e[i^1].flow+=res;
			if (used==flow) return used; 
		}
	}
	return used;
}

void dinic()
{
	while (bfs())
		maxf-=dfs(S,Inf);
}

int main()
{
	freopen("tower.in","r",stdin);
	freopen("tower.out","w",stdout);
	memset(head,-1,sizeof(head));
	S=M-1; T=M-2; tot=1;
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
			if (a[i][j]<0)
			{
				int maxn=0,id=-a[i][j];
				if (a[i][j]==-1 || a[i][j]==-2)
					for (int k=i+dx[id];k>0 && k<=n;k+=dx[id])
					{
						int flow=max(maxn,a[k][j])-maxn;
						maxf+=flow;
						add(S,ID(k,j,0),flow); add(ID(k,j,0),S,0);
						add(ID(k,j,0),ID(k-dx[id],j,0),Inf); add(ID(k-dx[id],j,0),ID(k,j,0),0);
						maxn=max(maxn,a[k][j]);
					}
				else
					for (int k=j+dy[id];k>0 && k<=m;k+=dy[id])
					{
						int flow=max(maxn,a[i][k])-maxn;
						maxf+=flow;
						add(ID(i,k,1),T,flow); add(T,ID(i,k,1),0);
						add(ID(i,k-dy[id],1),ID(i,k,1),Inf); add(ID(i,k,1),ID(i,k-dy[id],1),0);
						maxn=max(maxn,a[i][k]);
					}
			}
			else
			{
				add(ID(i,j,0),ID(i,j,1),Inf);
				add(ID(i,j,1),ID(i,j,0),0);
			}
	dinic();
	printf("%d",maxf);
	return 0;
}